An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
two
four
three
five
The correct Answer is:b
At x=0, path difference is 3λ. Hence,third-order maximum will be obtained. At x=∞, path difference is zero. Hence, zero-order maxima is obtained. In between, first - and second-order maxima will be obtained. First order maxima:
S2P−S1P=λ or √x2+9λ2−x=λ
or √x2+9λ2=x+λ
Squaring this, we get x2+9λ2=x2+λ2+2xλ
Solving this, we get x=4λ
Second-order maxima:
S2P−S1P=2λ or √x2+9λ2−x=2λ
or √x2+9λ2=(x+2λ)
Squaring both sides, we get
x2+9λ2=x2+4λ2+4xλ
Solving this, we get x=54λ=1.25λ
Hence, the desired x-corrdinates are
x=1.25λ and x=4λ
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
View SolutionTwo coherent sources Sf and S2 (in phase with ech other) are placed at a distance of 2λ as shown where λ is wavelength of sound. A detector moves on line AB parrallel to S1S2. If detector detects maximum intensity at finite distance from O at θ=±(πn). Find n

View SolutionTwo identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
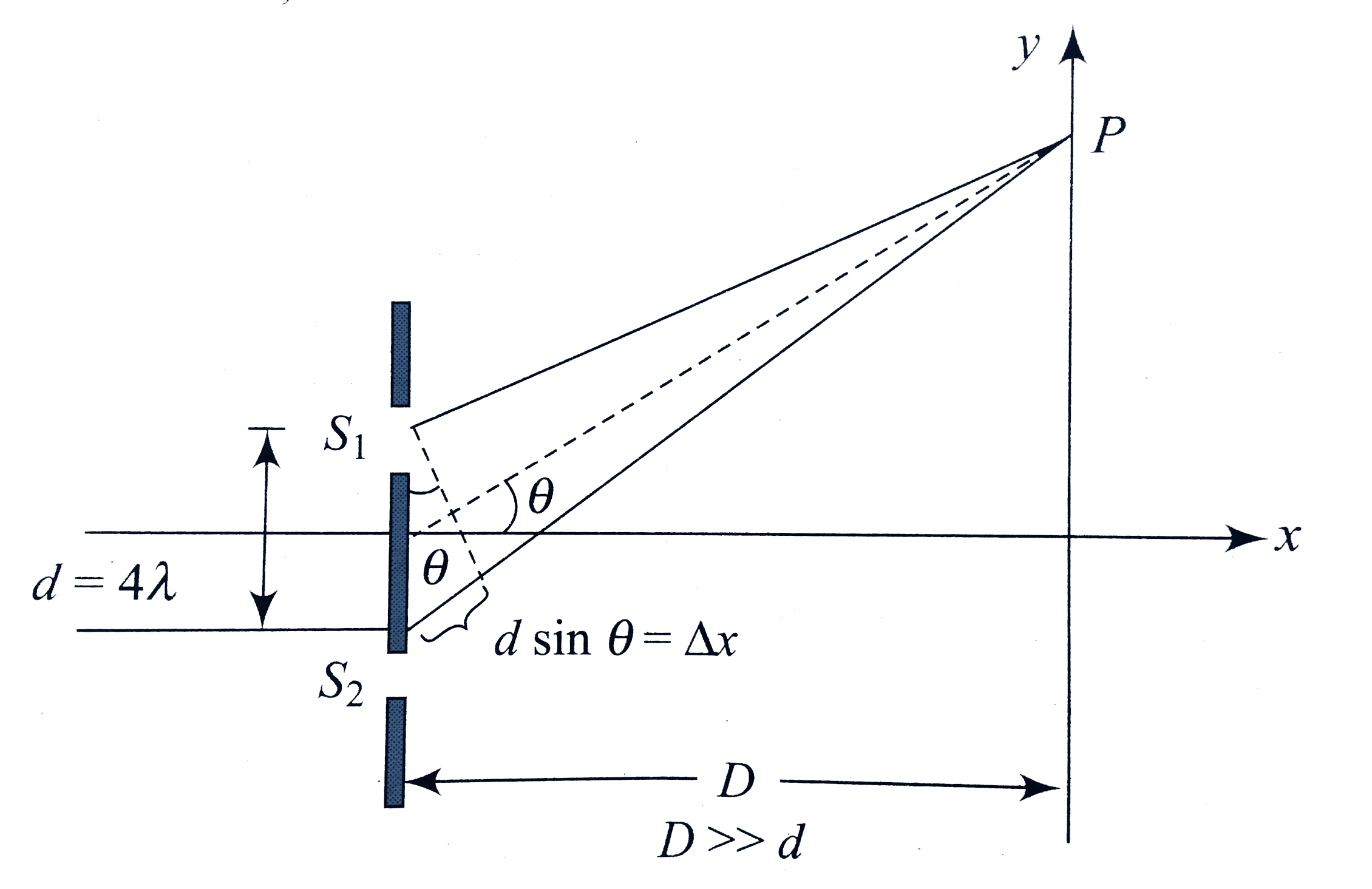
If a detector moves along the y-axis, what is the maximum number of minima observed?
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View SolutionTwo coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
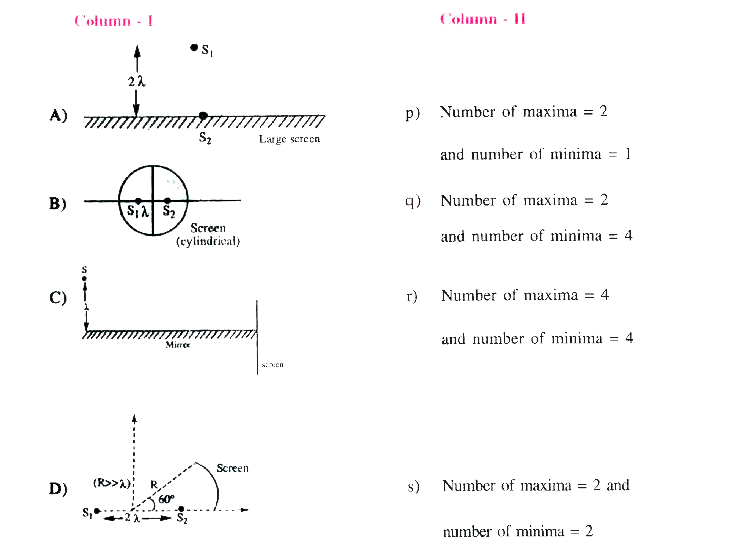
View SolutionS1 and S2 in List I represent coherent point sources, S represents a point source λ = wavelength of light emitted by the sources. Fringe pattern is observed on the screen. Exclude the position of source while detecting the fringe pattern.
View Solution
