In a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.
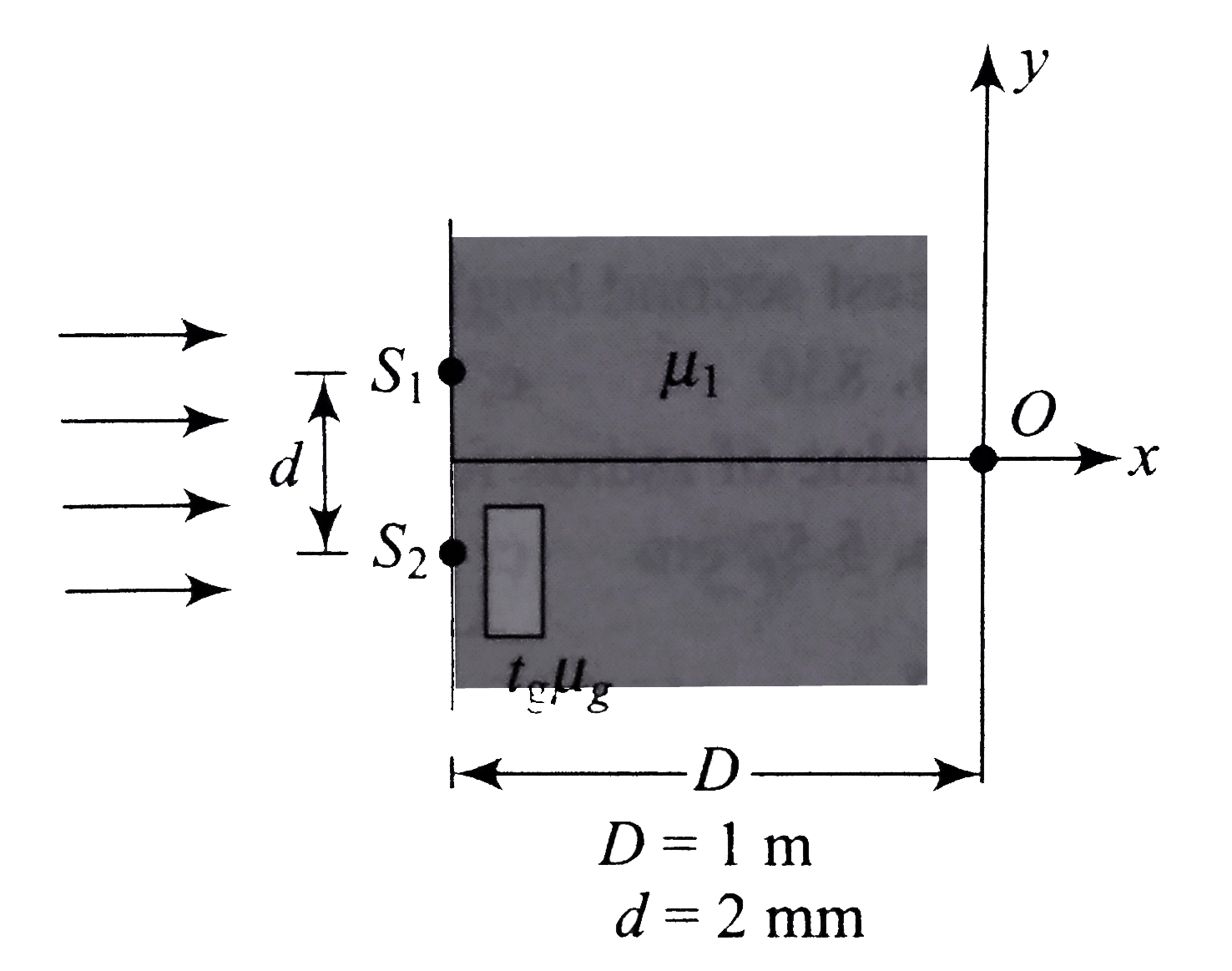
In a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as mu(1) = (5 // 2) - (T // 4) until it reaches s steady state value of 5 // 4. A glass plate of thickness 36 mu m and refractive index 3//2 is introduced in front of one of the slits. Find the time when central maxima is at point O. located symmetrically on the x-asix.
Find the time when central maxima is at point O. located symmetrically on the x-asix.

A

2 s

B

4 s

C

6 s

D

8 s

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:b

We consider a point P on the screen.
Optical path length,
[S1P]liquid=[μ1S1P]air
[S1P−t]liquid+tglass=μ[S1P−t]air+[μgt]air
=[μ1S2P+(μg−μ1)t]air
Hence, optical path difference at P,
Δx=[μ1S2P+(μg−μ1)t]−μ1S1P
=μ1(S1P−S1P)+(μg+μ1)t
For a point P at the screen in the absence of liquid,
S2P=S1P=ydD
If a liquid is filled,
[S2P−S1P]liquid=μ1ydD
Thus,
Δx=μ1ydD+[μg−μt]t
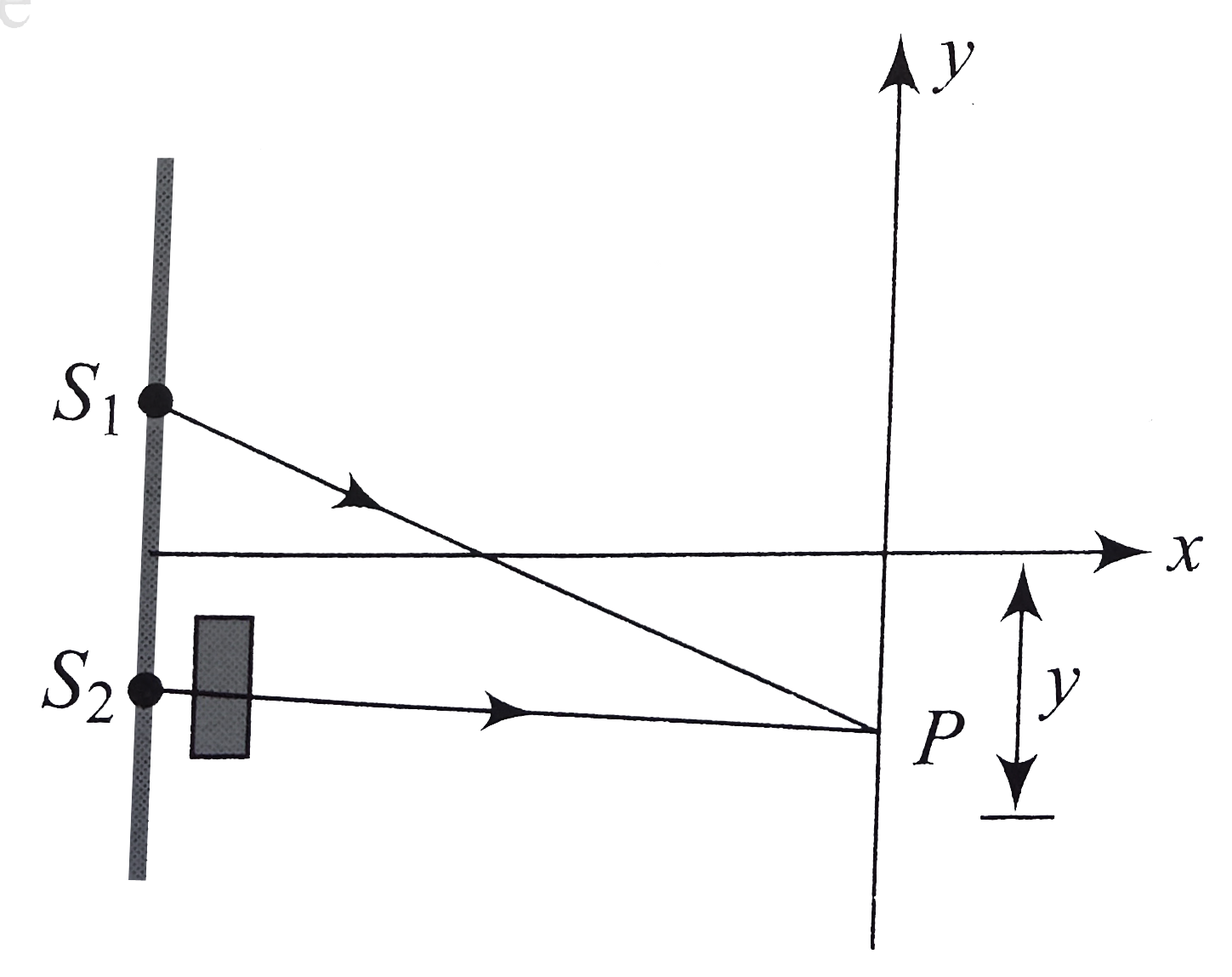
ocr_image
a. For central maxima,
Δx=0
y=[μg−μ1μ1]tDd=(4−T)tD(10−T)d
At Point O, y=0
Thus, T=4
b. Speed of central maxima,
v=∣∣∣dydt∣∣∣=6Dt(10−T)2d
Central maxima is at O at time t=4 s.
∴v=6Dt36D=1×36×10−66×2×10−3=3×10−3ms−1

Updated on:21/07/2023
|
Class 12PHYSICSWAVE OPTICS

Topper's Solved these Questions

Similar Questions