In YDSE arrangement as shown in the figure, fringes are seen on screen using monochromatic source S having wavelength 3000Å (in the air). S1andS2 are two slits separated by d = 1 mm and D = 1 m. Left of slits s1ands2 medium of refractive index n1=2 is present and to the right of S1andS2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1. The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.
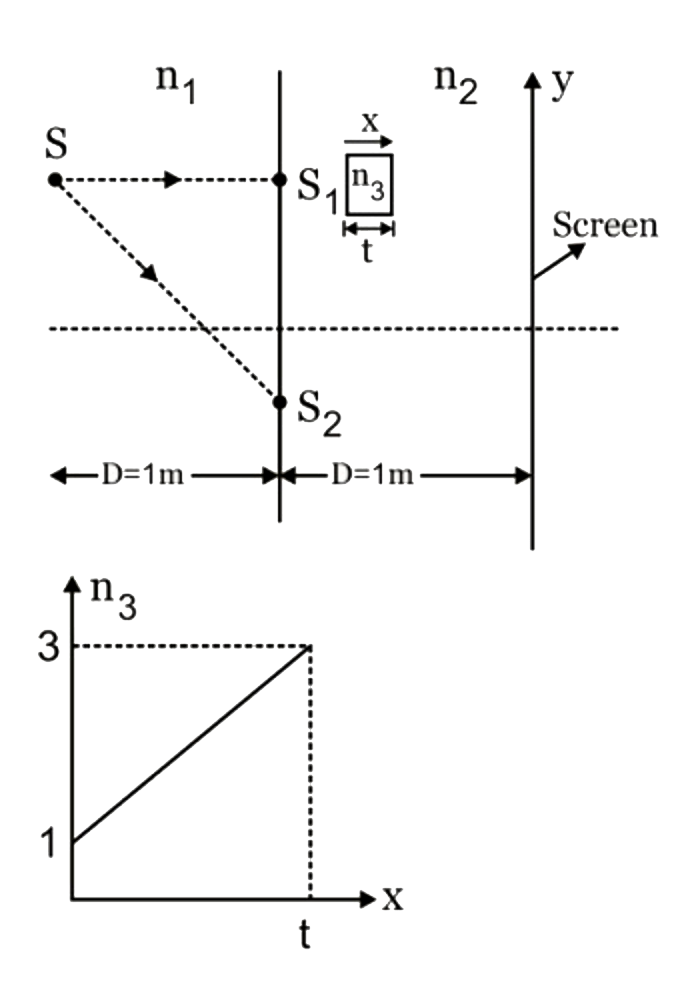
In order of get central maxima at the centre of the screen, the thickness of the slab (in μm) required is :
1/3 mm
−13mm
1/6 mm
−16mm
From previous equation :
0=1μm+3yd2D−0.5t
32ydD=−0.5μm
y=−(10−63)(1m1×10−3)=10−33=−13mm, below centre.
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionIn figure S is a monochromatic source of light emitting light of wavelength of wavelength lambda (in air). Light on slits S_(1) from S and then reaches in the slit S_(2) and S_(3) through a medium of refractive index mu_(1) . Light from slit S_(2) and S_(3) reaches the screen through a medium of refractive index mu_(3) . A thin transparent film of refractive index mu_(2) and thickness t is used placed in front of S_(2) . Point P is symmetrical w.r.t. S_(2) and S_(3) . Using the values d = 1 mm, D = 1 m, mu_(1) = 4//3 , mu_(2) = 3//2, mu_(3) = 9//5 , and t = (4)/(9) xx 10^(-5) m , a. find distance of central maxima from P, b. If the film in front of S_(2) is removed, then by what distance and in which direction will be central maxima shift ? .
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
View SolutionIn YDSE monochromatic light of wavelength 600 nm incident of slits as shown in figure.
_PHY_E01_002_Q01.png)
If S1S2=3mm,OP=11mm then
View SolutionIn YDSE arangement shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 overset(@)Delta (in air). S_(1) and S_(2) are two slits separate by d = 1mm and D = 1m . Left of slits S_(1) and S_(2) medium of refractive index mu_(1) = 2 is presernt refractive index mu_(2) = (3)/(2) is present. A thin slab of thickness 't' is placed in front of S_(1) . The refractive index of slab mu_(3) varies with distance from its starting face as shown in figure. If the thickness of the slab is selected 1mu m , then the position of the central maxima will be (y - coordinate)
View SolutionIn a YDSE experiment two slits S_(1) and S_(2) have separation of d=2mm the distance of the screen is D=(8)/(5) m source S starts moving from a very large distance towards S_(2) perpendicular to S_(1)S_(2) as shown in figure the wavelength of monochromatic light is 500 n. The number of maximas observed on the screen at point P as the moves towards S_(2) is
View SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :

View Solutionदो कला सम्बद्ध बिन्दु स्त्रोत S1 व S2 अल्प दूरी d से पृथक्कृत है। पर्दे पर प्राप्त फ्रिन्जे होगी:
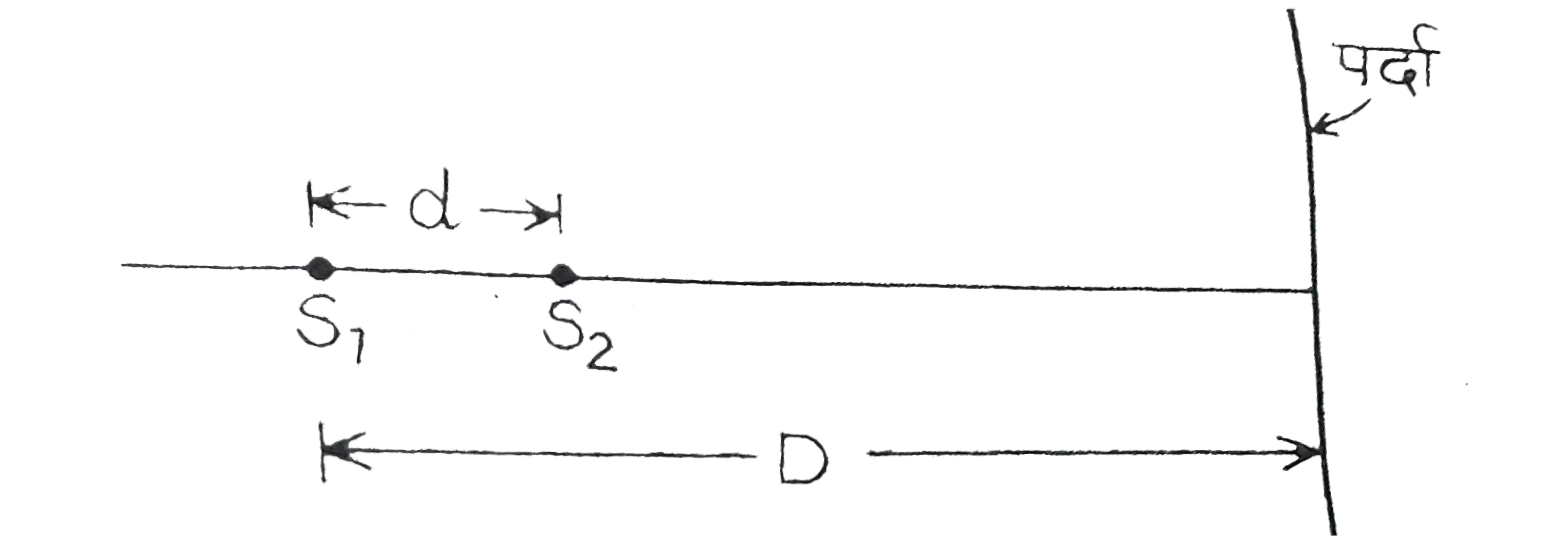
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
View Solutionदो आदर्श स्लिटो S1 व S2 को एक λ तरंगदैर्ध्य वाले आदर्श स्लिट स्त्रोत S द्वारा प्रकाशित किया जाता है। स्लिट S चित्रानुसार S2 के ठीक पीछे स्थित है। स्त्रोत स्लिट S एवं (S1,S2) स्लिटो के तलो के बीच की दूरी D है। एक पर्दा स्लिटो के तल से D दूरी पर स्थित है। स्लिटो (S1,S2) के बीच की दूरी (d) का न्यूनतम मान क्या होना चाहिए ताकि बिंदु O पर अदीप्त फ्रिन्ज प्राप्त हो?
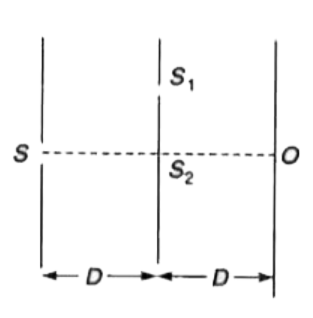
View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
View SolutionIn figure S is a monochromatic source of light emitting light of wavelength of wavelength λ (in air). Light on slits S1 from S and then reaches in the slit S2 and S3 through a medium of refractive index μ1. Light from slit S2 and S3 reaches the screen through a medium of refractive index μ3. A thin transparent film of refractive index μ2 and thickness t is used placed in front of S2. Point P is symmetrical w.r.t. S2 and S3. Using the values d=1mm,D=1m,μ1=4/3,
μ2=3/2,μ3=9/5, and t=49×10−5m,
a. find distance of central maxima from P,
b. If the film in front of S2 is removed, then by what distance and in which direction will be central maxima shift ?
 .
.
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
View SolutionIn a modified YDSE, sources S is kept in front of slit S_(1) . Find the phase difference at point O that is equidistant from slits S_(1) and S_(2) and point P that is in front of slit S_(1) in the following situations. A liquid of refractive index mu is filled between the screen and slits.
View SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength lamda is incident on identical slits S_(1) and S_(2) . There is another pair of indentical slits S_(3) and S_(4) which are having separation Z = (lamda D)/(2d) Point O is on the screen at the common perpendicular bisector of S_(1)S_(2) and S_(3) S_(4).I_(1) is the intensity at point O Now the board having slits S_(3)S_(4) is moved upward parallel to itself and perpendicular to line AO till slit S_(4) is on line AO and it is observed that now intensity at point O is I_(2) then (I_(2))/(I_(1)) is :
View Solution
