_S01_026_Q01.png)
In a YDSE experiment two slits S1 and S2 have separation of d=2mm the distance of the screen is D=85 m source S starts moving from a very large distance towards S2 perpendicular to S1S2 as shown in figure the wavelength of monochromatic light is 500 n. The number of maximas observed on the screen at point P as the moves towards S2 is
4001
3999
3998
4000
The correct Answer is:D
S1P−S2P=d22D=2×10−3×2×0−32×85=52λ (λ=500nm)
So when S is at ∞ there is 1st minima and when S is at S2 there is last minima because d/λ=4000
So the number of minima's will be 4001 and number of maxima's will be 4000.
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Example 9
1 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Example 10
1 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Example 7
1 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
In an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
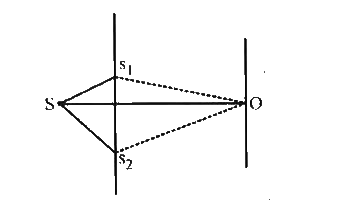
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View Solution
Knowledge Check
In the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
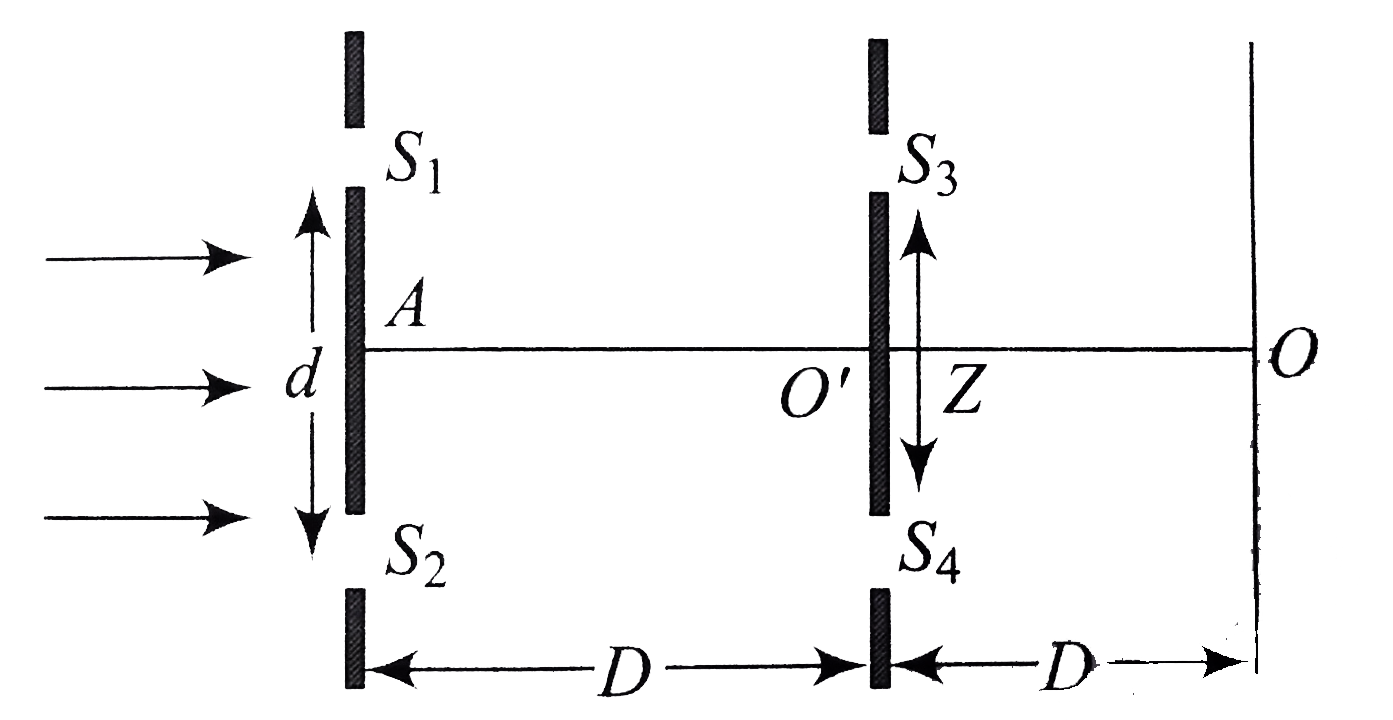
If a hole is made at O' on AO' O and the slit S4 is closed, then the ratio of the maximum to minimum observed on screen at O , if O'S3 is equal to λD4d, isA1BinfinityC34D4Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesIn a Young's double-slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is wavelength, the fringe width will be
AλθBλθC2λθDλ2θ
Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :

View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
View SolutionIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
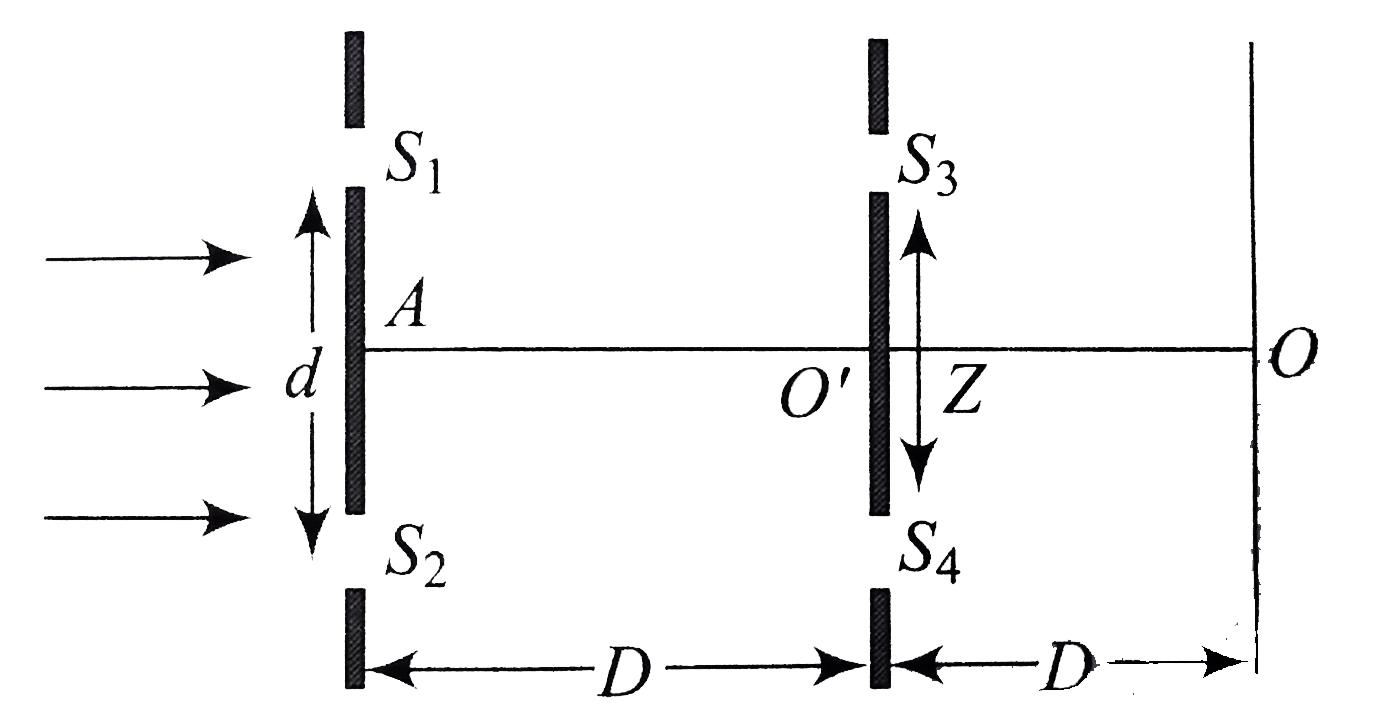
The minimum value of Z for which the intensity at O is zero is
View SolutionIn a Young's double slit experiment, the slit separation is 1mm and the screen is 1m from the slit. For a monochromatic light of wavelength 500nm, the distance of 3rd minima from the central maxima is
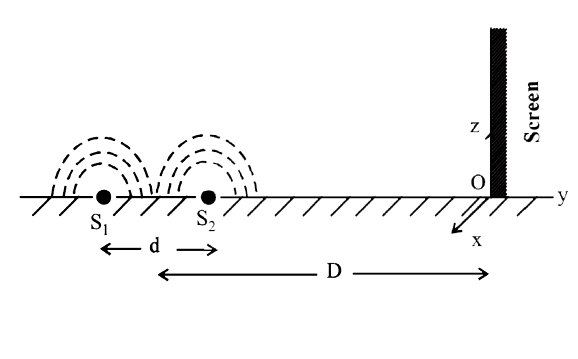
View SolutionWhile conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S1,S2) emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane (forz>0) at a distance D=3 m from the mid-point of S1,S2, as shown schematically in the figure. The distance between the sources d=0.6003mm. The origin O is at the intersection of the screen and the line joining S1S2. Which of the following is (are) true of the intensity pattern of the screen?
View Solution
