Two coherent sources S1 and S2 produce interference fringes. If a thin mica plate is introduced in the path of light from S1 then the central maximum
shift towards S2
shift towards S1
do not shift to any side
disappear
The correct Answer is:B
To solve the problem of how the introduction of a thin mica plate in the path of light from source S1 affects the central maximum in an interference pattern produced by two coherent sources S1 and S2, we can follow these steps:
Step 1: Understand the Interference Pattern
The interference pattern is formed due to the superposition of light waves from two coherent sources, S1 and S2. The central maximum occurs where the path difference between the two waves is zero.
Hint: Recall that the central maximum is the point of constructive interference where the path difference is zero.
Step 2: Introduce the Mica Plate
When a thin mica plate is introduced in the path of light from S1, it changes the optical path length of the light coming from that source. The optical path length is affected by the refractive index μ of the mica and the thickness t of the plate.
Hint: Remember that the optical path length is given by Optical Path Length=μ⋅t.
Step 3: Calculate the Additional Path Difference
The introduction of the mica plate introduces an additional path difference given by:
Δ=(μ−1)⋅t
This additional path difference shifts the effective position of the central maximum.
Hint: Consider how the additional path difference affects the existing path difference at the central maximum.
Step 4: Analyze the Effect on the Central Maximum
Since the central maximum originally had a path difference of zero, the introduction of the mica plate means that the path difference is no longer zero. To restore the condition for the central maximum (path difference of zero), the position of the central maximum must shift.
Hint: The central maximum will shift towards the source that has the additional optical path length (in this case, S1).
Step 5: Conclusion
Thus, the central maximum will shift towards S1 because the additional optical path length introduced by the mica plate effectively increases the path length from S1 relative to S2.
Final Answer: The central maximum shifts towards S1.
The interference pattern is formed due to the superposition of light waves from two coherent sources, S1 and S2. The central maximum occurs where the path difference between the two waves is zero.
When a thin mica plate is introduced in the path of light from S1, it changes the optical path length of the light coming from that source. The optical path length is affected by the refractive index μ of the mica and the thickness t of the plate.
The introduction of the mica plate introduces an additional path difference given by:
Δ=(μ−1)⋅t
This additional path difference shifts the effective position of the central maximum.
Since the central maximum originally had a path difference of zero, the introduction of the mica plate means that the path difference is no longer zero. To restore the condition for the central maximum (path difference of zero), the position of the central maximum must shift.
Thus, the central maximum will shift towards S1 because the additional optical path length introduced by the mica plate effectively increases the path length from S1 relative to S2.
Topper's Solved these Questions
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -IA (DIFFRACTION)
Explore 33 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -IA (POLARASATION)
Explore 29 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -III (POLARISITION)
Explore 10 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-III (Doppler effect :)
Explore 15 Videos
Similar Questions
Two coherent sources of intensities I1 and I2 produce an interference pattern. The maximum intensity in the interference pattern will be
View SolutionIn the arrangement shown, a screen is placed normal to the line joining the two point coherent sources S1 and S2. The interference pattern consist of concentric circles. λ is the wavelength of light (D>>d).

The phase difference of the interfering light at point P is
View Solution
Knowledge Check
The two coherent sources with intensity ratio β produce interference. The fringe visibility will be
A2√β1+βB2βC21+βD√β1+βIn the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
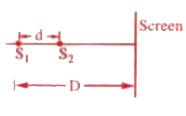
View SolutionIn Young's double slit experiment a mica plate of refractive index μ is introduced in the path of light coming from one of the slit . If the central bright fringe gets shifted to the point originally occupied by the fourth bright fringe, then the thickness of the mica plate will be (symbols have their usual meaning )
View SolutionInterference fringes were produced using light in a doulbe-slit experiment. When a mica sheet of uniform thickness and refractive index 1.6 (relative to air) is placed in the path of light from one of the slits, the central fringe moves through some distance. This distance is equal to the width of 30 interference bands if light of wavelength 4800 is used. The thickness (in μm) of mica is
View SolutionA monochromatic beam of light is used for the formation of fringes on a screen by illuminating the two slits in the Young,s double slit interference experiment. When a thin film of mic is interposed in the path of one of the interfering beams
View SolutionA double slit experiment is performed with light of wavelength 500nm. A thin film of thickness 2μm and refractive index 1.5 is introduced in the path of the upper beam. The location of the central maximum will
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View Solution

