A ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
60∘,30∘
30∘,60∘
sin−1(1√3),45∘
tan−1(√31),30∘
The correct Answer is:A
To solve the problem of finding the angle of incidence and angle of refraction of a ray of light incident on a glass plate at the polarizing angle, we can follow these steps:
Step 1: Understand the Polarizing Angle
The polarizing angle (also known as Brewster's angle) is the angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. The relationship between the polarizing angle (p) and the refractive index (μ) of the material is given by:
tan(p)=μ
Step 2: Given Data
We are given that the refractive index of the glass plate is:
μ=√3
Step 3: Calculate the Polarizing Angle
Using the formula for the polarizing angle:
tan(p)=√3
To find the polarizing angle (p), we take the arctangent:
p=tan−1(√3)
Step 4: Determine the Angle of Incidence
From trigonometric values, we know:
tan(60∘)=√3
Thus, the polarizing angle is:
p=60∘
So, the angle of incidence (i) is:
i=p=60∘
Step 5: Calculate the Angle of Refraction
According to Snell's law, the angle of refraction (r) can be found using:
r=90∘−p
Substituting the value of p:
r=90∘−60∘=30∘
Conclusion
Thus, the angle of incidence is 60∘ and the angle of refraction is 30∘.
Final Answer:
- Angle of Incidence (i) = 60∘
- Angle of Refraction (r) = 30∘
---
The polarizing angle (also known as Brewster's angle) is the angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. The relationship between the polarizing angle (p) and the refractive index (μ) of the material is given by:
tan(p)=μ
We are given that the refractive index of the glass plate is:
μ=√3
Using the formula for the polarizing angle:
tan(p)=√3
To find the polarizing angle (p), we take the arctangent:
p=tan−1(√3)
From trigonometric values, we know:
tan(60∘)=√3
Thus, the polarizing angle is:
p=60∘
So, the angle of incidence (i) is:
i=p=60∘
According to Snell's law, the angle of refraction (r) can be found using:
r=90∘−p
Substituting the value of p:
r=90∘−60∘=30∘
Thus, the angle of incidence is 60∘ and the angle of refraction is 30∘.
- Angle of Incidence (i) = 60∘
- Angle of Refraction (r) = 30∘
Topper's Solved these Questions
Similar Questions
A light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
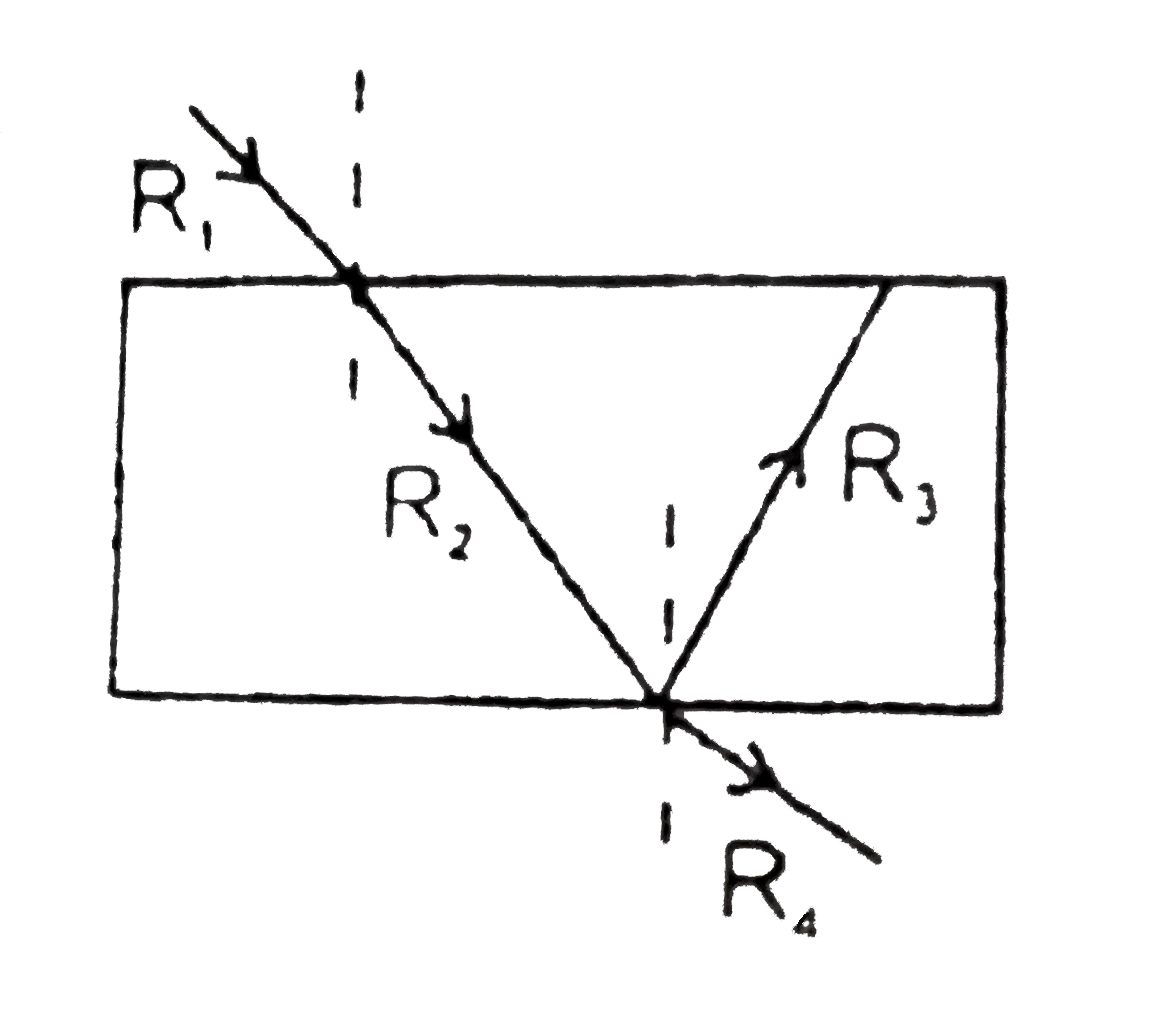
View Solution
Knowledge Check
A beam of light is incident at the polarizing angle of 35∘ on a certain glass plate. The refractive index of the glass plate is:
Asin35∘Btan35∘Ctan55∘Dsin55∘
A ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :

View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionExplain refraction. Draw a diagram and explain incident ray, refracted ray, angle of incidence, and angle of refraction.
View SolutionA ray of monochromatic light is incident on the refracting face of a prism (angle 75∘0 . It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the prism is √2 , then the angle of incidence on the first of the prism is
View SolutionA ray of light is incident on a rectangular plate at an angle of incidence 60∘. The light ray suffers a deviation which is 25% of the angle of incidence. The refractive index of the glass will be
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?

View SolutionA ray of light passes from glass, having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
View Solution
