Two coherent light sources and are apart from each other. The screen is placed at a distance of from the sources. The width of the fringes on the screen should be
0.015 cm
0.025 cm
0.010 cm
0.030 cm
The correct Answer is:A
To find the width of the fringes on the screen, we can use the formula for fringe width (β) in a double-slit interference pattern:
β=d⋅λD
where:
- β is the fringe width,
- d is the distance between the two coherent light sources (slits),
- λ is the wavelength of the light,
- D is the distance from the slits to the screen.
Step 1: Identify the given values
- Wavelength λ=6000Å=6000×10−10m=6000×10−8cm=6×10−5cm
- Distance between the slits d=1mm=0.1cm
- Distance to the screen D=25cm
Step 2: Substitute the values into the formula
Now, substituting the values into the formula:
β=D⋅λd
Substituting the known values:
β=25cm⋅6×10−5cm0.1cm
Step 3: Calculate the fringe width
Calculating the numerator:
25⋅6=150
So we have:
β=150×10−5cm0.1cm
Now, dividing by 0.1:
β=1500×10−5cm=1.5×10−2cm
Step 4: Convert to a more convenient unit
To express this in centimeters:
β=0.015cm
Final Answer
The width of the fringes on the screen is 0.015cm.
---
- β is the fringe width,
- d is the distance between the two coherent light sources (slits),
- λ is the wavelength of the light,
- D is the distance from the slits to the screen.
- Wavelength λ=6000Å=6000×10−10m=6000×10−8cm=6×10−5cm
- Distance between the slits d=1mm=0.1cm
- Distance to the screen D=25cm
Now, substituting the values into the formula:
Calculating the numerator:
To express this in centimeters:
The width of the fringes on the screen is 0.015cm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.54
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.55
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.52
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
The distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
View SolutionTwo coherent sources are 0.3 mm apart. They are 0.9m away from the screen. The second dark fringe is at a distance of 0.3cm from the centre. Find the distance of fourth bright fringe from the centre. Also, find the wavelength of light used.
View SolutionA lens of focal length 20.0 cm and aperture radius 2.0cm is placed at a distance 30.cm from a point source of light. On the other side a screen is placed at a distance 50.0cm from the lens. The radius of spot of light formed on screen is (neglect spherical abberation through lens)
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionIn Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength 6000Å The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
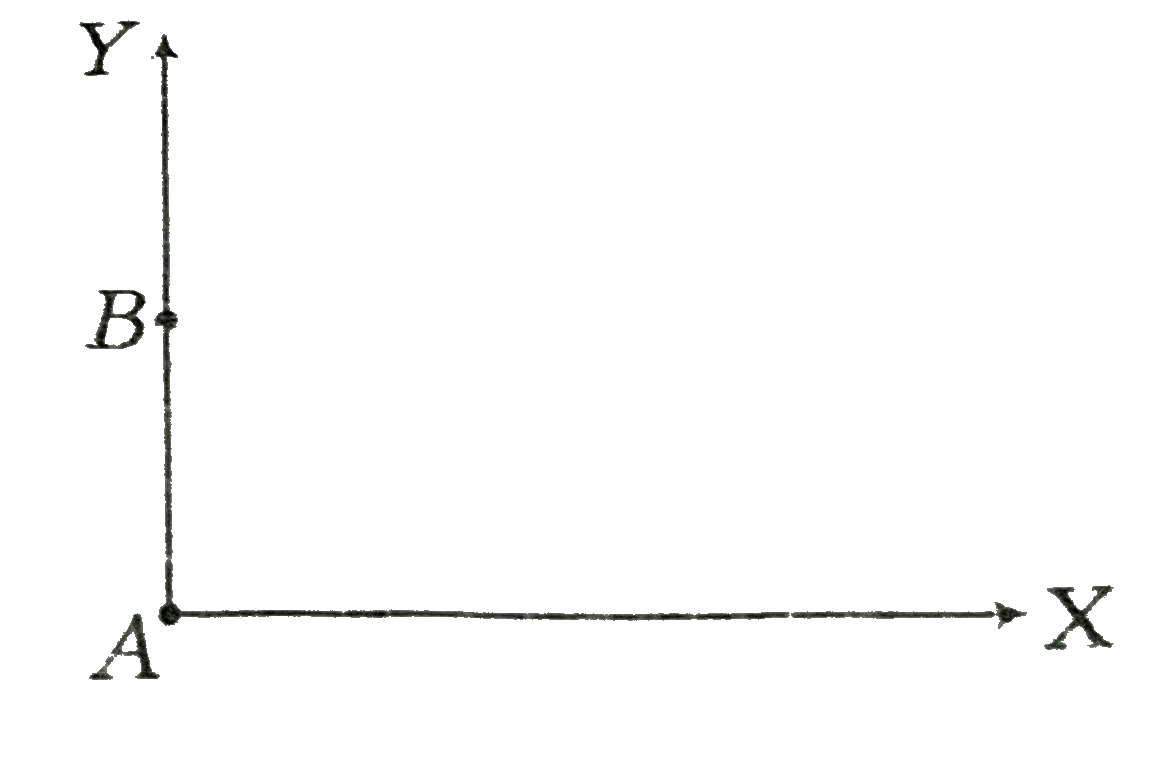
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
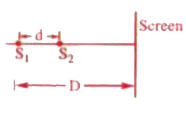
View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is

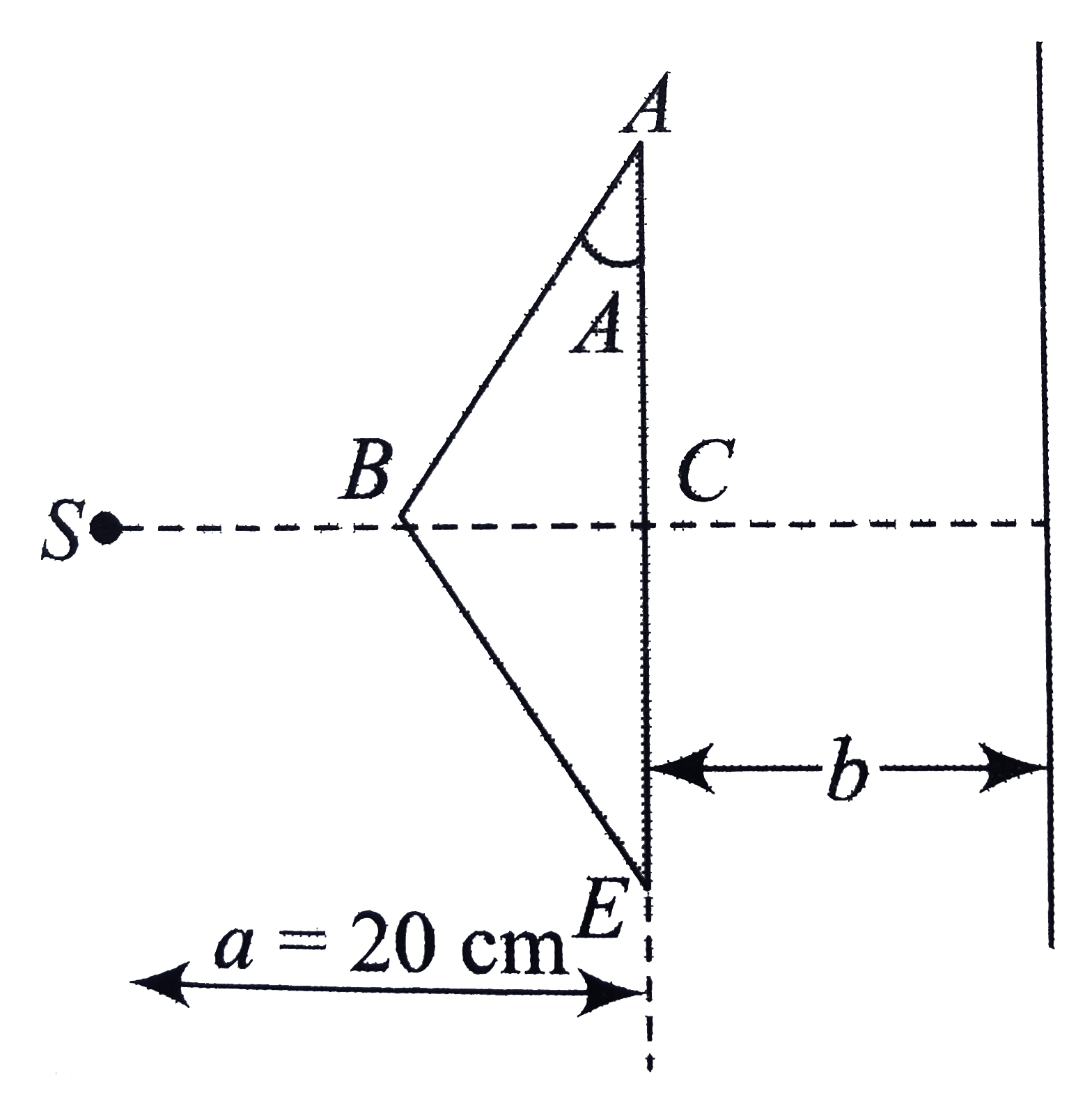
View SolutionTwo small angled transparent prisms (each or refracting angle A=1∘) are so placed that their bases coincide, so that common base is BC. This device is called Fresnel's biprism and is used to obtain coherent sources of a point source S illuminated by monochromatic light of wavelength 6000Å placed at a distance a=20 cm. Calculate the separation between coherent sources. If a screen is placed at a distance b=80 cm. from the device, what ist the finge which of fringes obtained (Refractive index of material of each prism =1.5.)
View Solution
