A lens of focal length 20.0 cm and aperture radius 2.0cm is placed at a distance 30.cm from a point source of light. On the other side a screen is placed at a distance 50.0cm from the lens. The radius of spot of light formed on screen is (neglect spherical abberation through lens)
1/2cm
1/3cm
1/5cm
1.0cm
The correct Answer is:b.
To solve the problem step by step, we will follow these steps:
Step 1: Understand the lens formula
The lens formula relates the object distance (u), image distance (v), and focal length (f) of a lens. The formula is given by:
1f=1v−1u
Step 2: Identify the given values
From the problem, we have:
- Focal length f=20cm
- Object distance u=−30cm (negative because the object is on the same side as the incoming light)
- Aperture radius R=2cm
Step 3: Substitute the values into the lens formula
We need to find the image distance v. Rearranging the lens formula gives:
1v=1f+1u
Substituting the known values:
1v=120+1−30
Step 4: Calculate the right-hand side
To add these fractions, we need a common denominator. The least common multiple of 20 and 30 is 60:
120=360,1−30=−260
So,
1v=360−260=160
Step 5: Find the image distance v
Taking the reciprocal gives:
v=60cm
Step 6: Determine the position of the image
Since the screen is placed at a distance of 50 cm from the lens, and the image distance v=60cm indicates that the image is formed 10 cm behind the screen.
Step 7: Calculate the radius of the spot of light on the screen
Using similar triangles, we can find the radius of the spot of light on the screen. The triangles formed by the rays of light passing through the lens and hitting the screen are similar.
Let h be the radius of the spot of light on the screen. From the similar triangles:
h10=260
Cross-multiplying gives:
h=260×10
h=2060=13cm
Final Answer
The radius of the spot of light formed on the screen is:
13cm
The lens formula relates the object distance (u), image distance (v), and focal length (f) of a lens. The formula is given by:
1f=1v−1u
From the problem, we have:
- Focal length f=20cm
- Object distance u=−30cm (negative because the object is on the same side as the incoming light)
- Aperture radius R=2cm
We need to find the image distance v. Rearranging the lens formula gives:
1v=1f+1u
Substituting the known values:
1v=120+1−30
To add these fractions, we need a common denominator. The least common multiple of 20 and 30 is 60:
120=360,1−30=−260
So,
1v=360−260=160
Taking the reciprocal gives:
v=60cm
Since the screen is placed at a distance of 50 cm from the lens, and the image distance v=60cm indicates that the image is formed 10 cm behind the screen.
Using similar triangles, we can find the radius of the spot of light on the screen. The triangles formed by the rays of light passing through the lens and hitting the screen are similar.
h10=260
Cross-multiplying gives:
h=260×10
h=2060=13cm
The radius of the spot of light formed on the screen is:
13cm
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Assertion-Reasoninig
Explore 2 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Linked Comprehension
Explore 51 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Subjective
Explore 26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
Similar Questions
An object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionFind distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A point source of light is placed at a distance of 2f from a converging lens of focal length f. The intensity onteh other side of the lens is maximum at a distance
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionAn object of length 2.0 cm is placed perpendicular to the principal axis of a convex lens of focal length 12 cm. Find the size of the image of the object is at a distance of 8.0 cm from the lens.
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
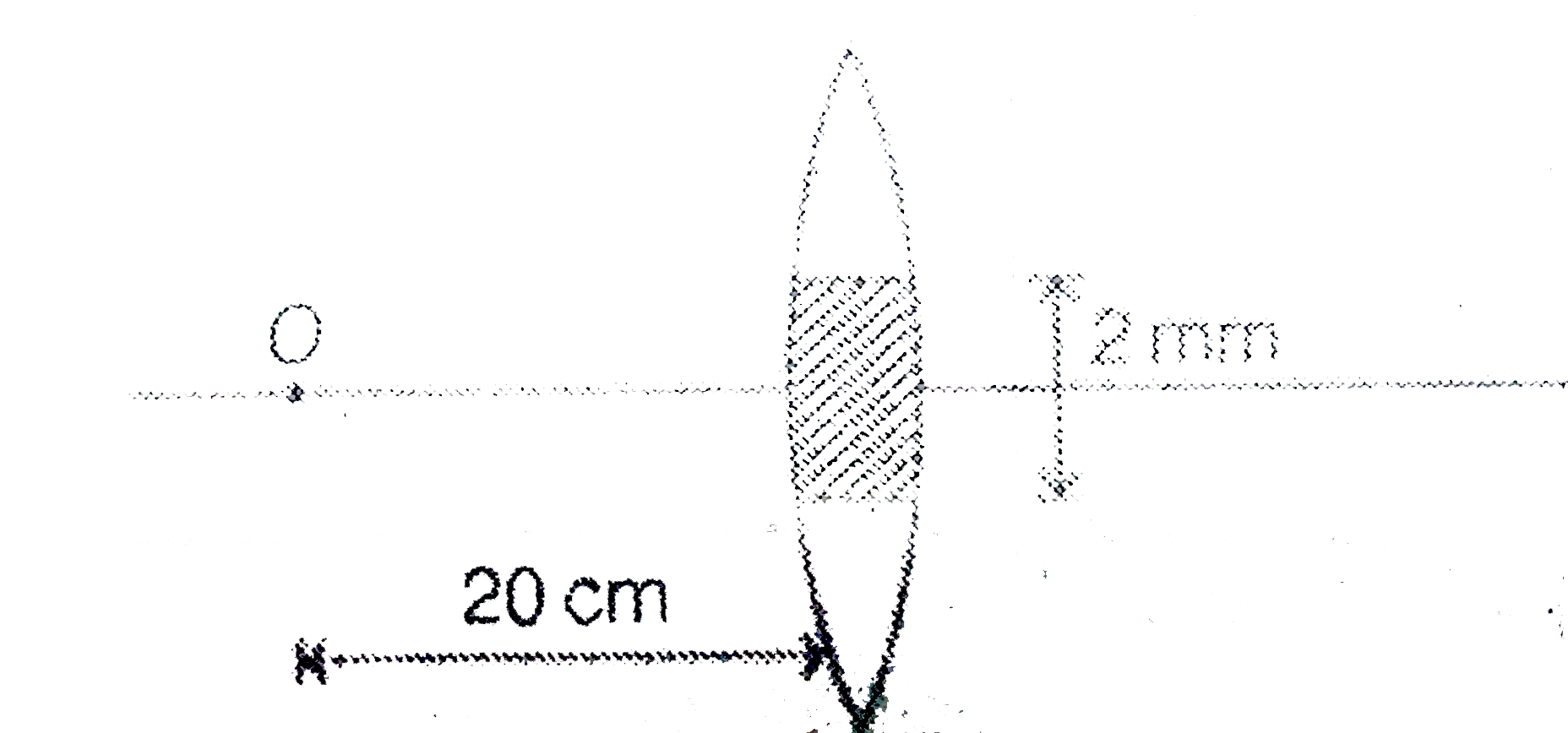
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionA convex lens of diameter 8.0 cm is used to focus a parallel beam of light of wavelength 620 nm. If the light be focused at a distance of 20 cm from the lens, what would be the radius of the central bright spot formed ?
View Solution