A convex lens of diameter 8.0 cm is used to focus a parallel beam of light of wavelength 620 nm. If the light be focused at a distance of 20 cm from the lens, what would be the radius of the central bright spot formed ?
The correct Answer is:A, C
To find the radius of the central bright spot formed by a convex lens when focusing a parallel beam of light, we can use the formula for the radius of the central bright spot in diffraction patterns:
r=1.22λDd
Where:
- r is the radius of the central bright spot,
- λ is the wavelength of the light,
- D is the distance from the lens to the screen where the spot is formed,
- d is the diameter of the lens.
1. Identify the given values:
- Diameter of the lens, d=8.0cm=8×10−2m
- Wavelength of the light, λ=620nm=620×10−9m
- Distance from the lens to the screen, D=20cm=20×10−2m
2. Substitute the values into the formula:
r=1.22×(620×10−9)×(20×10−2)8×10−2
3. Calculate the numerator:
- Calculate 1.22×620×10−9:
1.22×620=756.4×10−9
- Now multiply by 20×10−2:
756.4×10−9×20×10−2=15128×10−11=1.5128×10−7m
4. Calculate the denominator:
- The denominator is 8×10−2.
5. Divide the numerator by the denominator:
r=1.5128×10−78×10−2=1.89×10−6m
6. Final result for the radius of the central bright spot:
The radius of the central bright spot is approximately:
r≈1.89μm
- r is the radius of the central bright spot,
- λ is the wavelength of the light,
- D is the distance from the lens to the screen where the spot is formed,
- d is the diameter of the lens.
- Diameter of the lens, d=8.0cm=8×10−2m
- Wavelength of the light, λ=620nm=620×10−9m
- Distance from the lens to the screen, D=20cm=20×10−2m
r=1.22×(620×10−9)×(20×10−2)8×10−2
- Calculate 1.22×620×10−9:
1.22×620=756.4×10−9
- Now multiply by 20×10−2:
756.4×10−9×20×10−2=15128×10−11=1.5128×10−7m
- The denominator is 8×10−2.
r=1.5128×10−78×10−2=1.89×10−6m
The radius of the central bright spot is approximately:
r≈1.89μm
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -2
10 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
Similar Questions
Light of wavelength 560 nm goes through a pinhole of diameter 0.20 mm and falls on a wall at a distance of 2.00 m. What will be the radius of the central bright spot formed on the wall ?
View SolutionA beam of light of wavelength 590 nm is focused by a converging lens of diameter 10.0 cm at a distance of 20 cm from it. find the diameter of the disc image formed.
View Solution
Knowledge Check
The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convax lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image.
A1.25cmB2.5cmC1.05cmD2cm
A beam of light of wavelength 590 nm is focused by a converging lens of diameter 10.0 cm at a distance of 20 cm from it. find the diameter of the disc image formed.
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
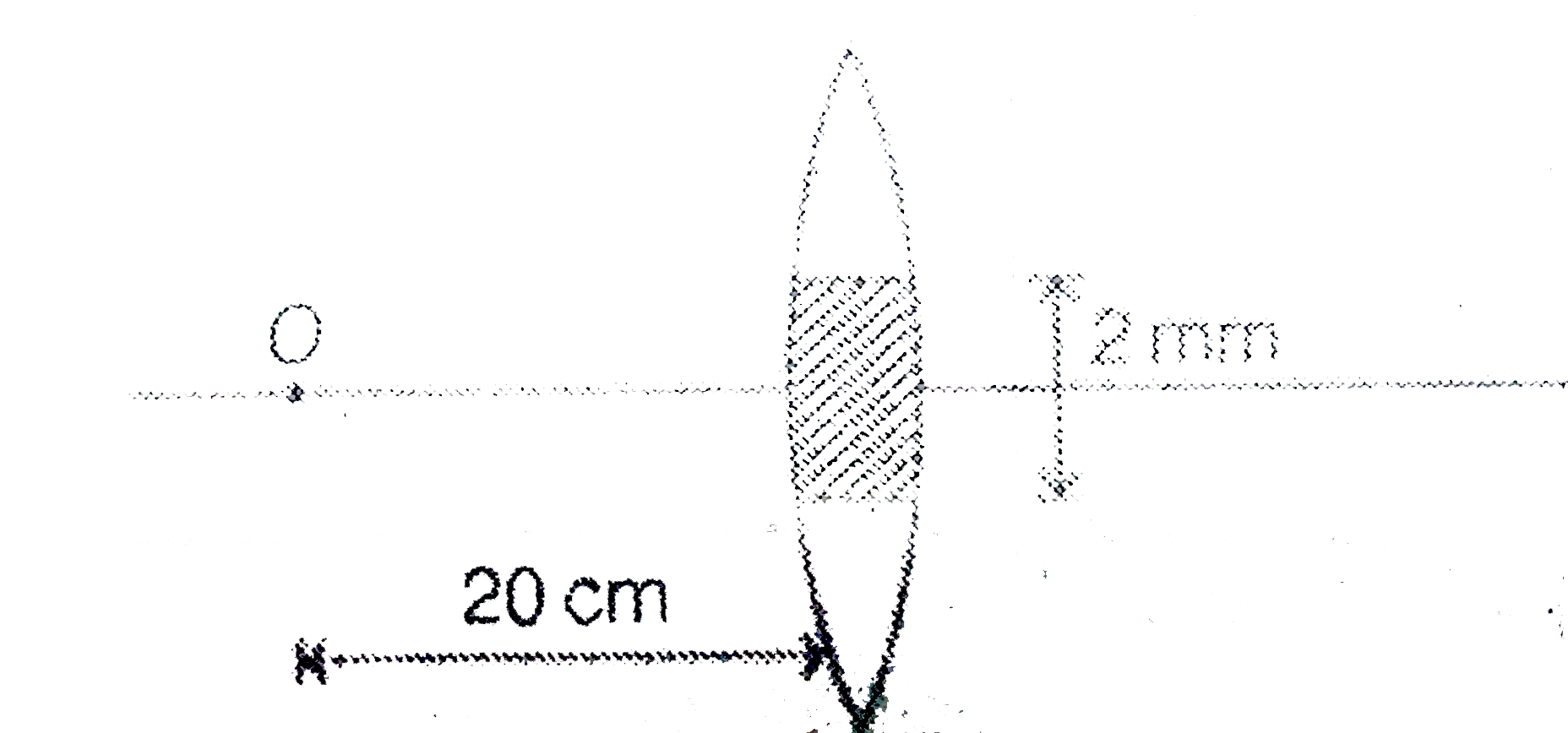
View SolutionA single slit of width 0.1mm is illuminated by parallel light of wavelength 6000Å, and diffraction bands are observed on a screen 40cm from the slit. The distance of third dark band from the central bright band is:
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionA lens of focal length 20.0 cm and aperture radius 2.0cm is placed at a distance 30.cm from a point source of light. On the other side a screen is placed at a distance 50.0cm from the lens. The radius of spot of light formed on screen is (neglect spherical abberation through lens)
View SolutionA convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What will be the linear magnification produced convex lens and concave lens individually ?
View SolutionAn object is put at a distance of 5cm from the first focus of a convex lens of focal length 10cm. If a real image is formed, its distance from the lens will be
View Solution
