The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of λ, d and D where the symbols have their usual meanings
The correct Answer is:A, B, D
To find the line-width of a bright fringe in a Young's double slit experiment, we will follow these steps:
Step 1: Understanding the Concept of Intensity
In a Young's double slit experiment, the intensity of light at a point on the screen is given by the interference of light waves coming from the two slits. The maximum intensity occurs at the central maximum (bright fringe).
Step 2: Maximum Intensity
Let the maximum intensity at the central bright fringe be denoted as I0.
Step 3: Condition for Half Maximum Intensity
The line-width of a bright fringe is defined as the distance between the two points on either side of the central maximum where the intensity falls to half of the maximum intensity. Thus, we need to find the positions where the intensity I is equal to I02.
Step 4: Expression for Intensity
The intensity at a point on the screen in a double slit experiment can be expressed as:
I=I0cos2(πdsinθλ)
where d is the distance between the slits, λ is the wavelength of light, and θ is the angle of the point from the central maximum.
Step 5: Finding the Angle for Half Maximum
Setting I=I02:
I02=I0cos2(πdsinθλ)
This simplifies to:
cos2(πdsinθλ)=12
Taking the square root gives:
cos(πdsinθλ)=1√2
This implies:
πdsinθλ=π4or3π4
Step 6: Finding the Positions on the Screen
For small angles, sinθ≈tanθ≈yD where y is the distance from the central maximum on the screen and D is the distance from the slits to the screen. Thus:
πdyDλ=π4
Solving for y:
y=λD4d
Similarly, for the other side:
πdy′Dλ=3π4
Solving for y′:
y′=3λD4d
Step 7: Calculating the Line-width
The line-width W is the distance between these two points:
W=y′−y=3λD4d−λD4d=2λD4d=λD2d
Final Answer
Thus, the line-width of a bright fringe in a Young's double slit experiment is:
W=λD2d
---
In a Young's double slit experiment, the intensity of light at a point on the screen is given by the interference of light waves coming from the two slits. The maximum intensity occurs at the central maximum (bright fringe).
Let the maximum intensity at the central bright fringe be denoted as I0.
The line-width of a bright fringe is defined as the distance between the two points on either side of the central maximum where the intensity falls to half of the maximum intensity. Thus, we need to find the positions where the intensity I is equal to I02.
The intensity at a point on the screen in a double slit experiment can be expressed as:
I=I0cos2(πdsinθλ)
where d is the distance between the slits, λ is the wavelength of light, and θ is the angle of the point from the central maximum.
Setting I=I02:
I02=I0cos2(πdsinθλ)
This simplifies to:
cos2(πdsinθλ)=12
Taking the square root gives:
cos(πdsinθλ)=1√2
This implies:
πdsinθλ=π4or3π4
For small angles, sinθ≈tanθ≈yD where y is the distance from the central maximum on the screen and D is the distance from the slits to the screen. Thus:
πdyDλ=π4
Solving for y:
y=λD4d
Similarly, for the other side:
πdy′Dλ=3π4
Solving for y′:
y′=3λD4d
The line-width W is the distance between these two points:
W=y′−y=3λD4d−λD4d=2λD4d=λD2d
Thus, the line-width of a bright fringe in a Young's double slit experiment is:
W=λD2d
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -2
10 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
Similar Questions
Draw a neat labelled diagram of Young.s Double Slit experiment. Show that β=λDd, where the terms have their usual meaning (either for bright or dark fringe).
View SolutionDraw a neat labelled diagram of Young.s Double Slit experiment. Show that β=λDd, where the terms have their usual meaning (either for bright or dark fringe).
View SolutionFind the angular fringe width in Young's double slit experiment using a monochromatic light of wavelength 500 nm when the slits are separated by 2.5 mm.
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionHow does the fringe width, in Young's double-slit experiment, change when the distance of separation between the slits and screen is doubled ?
View SolutionIn Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionFollowing figure shows the positions of the first bright fringes B1andB2 on either side of the central bright fringe O in Young.s double slit experiment. Find the wavelength of monochromatic light used.
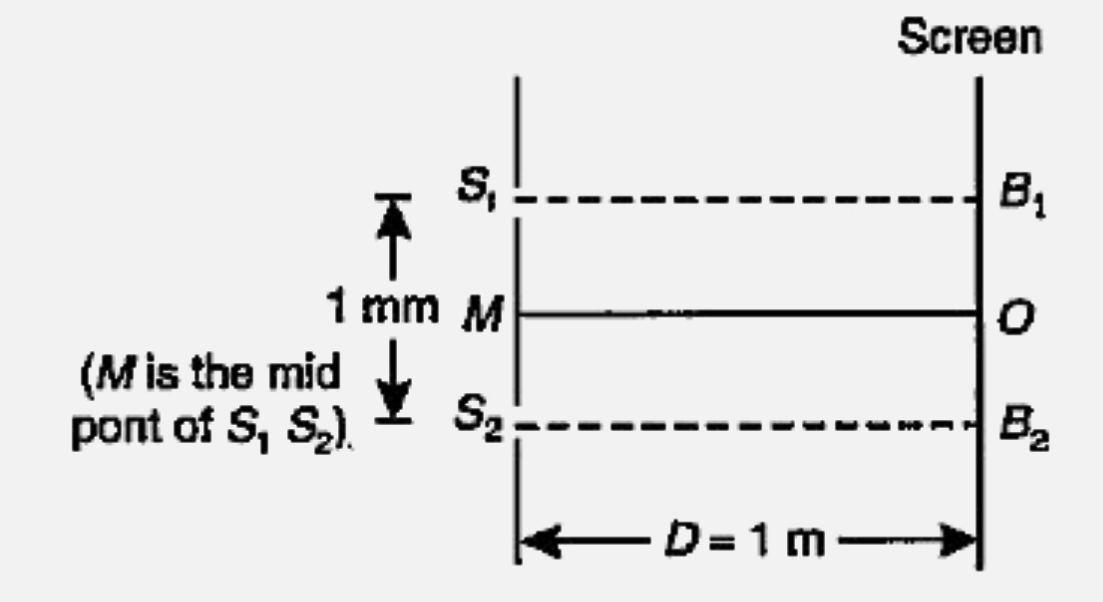
View SolutionIn a Young's double slit experiment, D equals the distance of screen and d is the separation between the slits. The distance of the nearest point to the central maximum where the intensity is same as that due to a single slit is equal to
View SolutionDraw a neat labelled diagram of Young.s Double Slit experiment. Show that β=λDd, where the terms have their usual meaning (either for bright or dark fringe).
View Solution
