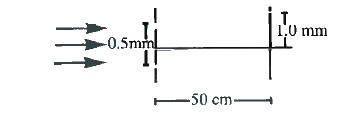
White coherent light (400nm−700nm) is sent through the slits of a YDSE. d=0.5mm, D=50 cm. There is a hole in the screen at a point 1.0mm away (along the width of the fringes) from the central line.
(a) Which wavelength will be absent in the light coming from the hole?
(b) Which wavelength(s) will have a strong intensity?

The correct Answer is:A, B, D
Given that λ=(400nm→700nm).,<br>d=0.5mm=0.5xx10^-3m<br>D=50cm=0.5m
and on the screen yn=1mm=1×10−3m
a. We know that for zero intensity (dark fringe)
yn=(2n+1)2λnDd
where n=0,1,2,……..
→λn=2(2n+1)yndD
=2(2n+1)×(10−3×()0.05)×10−3(0.5)
=2(2n+1)×10−6m
=2(2n+1)×103nm
If n=1
λ1=(23)×1000
=667nm
Ifn=1
λ2=(25)×1000
=400nm
So the light waves of wavelength 400 nm and 667 nm will be absent from the outcoming light.
b. For strong intensity (bright fringes) at the hold
yn=nλnDd
λn=yndnD
whenn=1,λ1=yndD
=10−3×(0.5)×10−30.5
=10−3m=100nm
1000 nm is not present in the range 400 nm -700 nm
Again when n=2
λ2=yn=ynd2D=500nm
So the wavelength which will have strong intensity is 500 nm.
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -2
10 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
Similar Questions
White coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
View SolutionWhite coherent light (400 nm- 700 nm) is sent through the slits of a young.s double slit experiment. The separation between the slits is 0.5mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1 mm from the centre.
In the above problem which wavelength have a strong intensity at the hole?
View SolutionIn this problem , which wavelength (s) will have a strong intensity if light have wavelength 400 nm-700 nm?
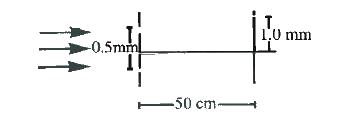
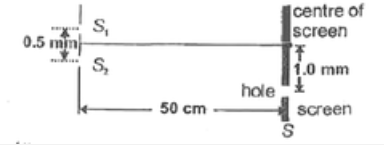
View SolutionIn young's double slit experiment shown in figure, S1andS2 are coherent sources and S in the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
View SolutionA double slit of separation 1.5 mm is illuminated by white light (between 4000 and 8000 Å). On a screen 120 cm away colored interference pattern is formed. If a pinhole is made on this screen at a distance of 3.0 mm from the central white fringe, some wavelengths will be absent in the transimitted light. Find the second longest wavelength (in Å) which will be absent in the transmitted light.
View SolutionWith two slits spaced 0.2 mm apart and a screen at a distance of 1 m, the third bright fringe is found to be at 7.5 mm from the central fringe. The wavelength of light used is
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View SolutionLight from a sodium lamp. λ. = 600 nm, is diffracted by a slit of width d= 0.60 mm. The distance from the slit to the screen is D = 0.60 m. Then, the width of the central maximum is
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View Solution
