Question

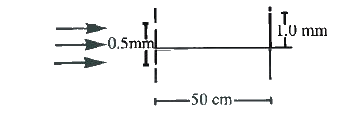
White coherent light (400 nm- 700 nm) is sent through the slits of a young.s double slit experiment. The separation between the slits is $0.5mm$ and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1 mm from the centre.
In the above problem which wavelength have a strong intensity at the hole?

Explanation

To solve the problem, we need to determine which wavelengths of light will produce a strong intensity at a point 1 mm from the center of the screen in a Young's double slit experiment. We will use the formula for the position of bright fringes in the interference pattern.

1. Identify Given Values:
- Wavelength range: \( \lambda = 400 \, \text{nm} \) to \( 700 \, \text{nm} \)
- Slit separation: \( d = 0.5 \, \text{mm} = 0.5 \times 10^{-3} \, \text{m} \)
- Distance to screen: \( D = 50 \, \text{cm} = 0.5 \, \text{m} \)
- Distance from center to the hole: \( Y_n = 1 \, \text{mm} = 1 \times 10^{-3} \, \text{m} \)

2. Use the Formula for Bright Fringes:
The position of the \( n^{th} \) bright fringe is given by:
\( Y_n = \frac{n \lambda D}{d} \)
Rearranging this formula to find the wavelength \( \lambda \):
\( \lambda = \frac{Y_n d}{n D} \)

3. Calculate for \( n = 1 \):
Substitute \( n = 1 \):
\( \lambda_1 = \frac{(1 \times 10^{-3} \, \text{m}) \times (0.5 \times 10^{-3} \, \text{m})}{1 \times 0.5 \, \text{m}} \)
Simplifying this:
\( \lambda_1 = \frac{0.5 \times 10^{-6}}{0.5} = 1 \times 10^{-6} \, \text{m} = 1000 \, \text{nm} \)
Since \( 1000 \, \text{nm} \) is outside the given range (400 nm to 700 nm), we discard this wavelength.

4. Calculate for \( n = 2 \):
Substitute \( n = 2 \):
\( \lambda_2 = \frac{(1 \times 10^{-3} \, \text{m}) \times (0.5 \times 10^{-3} \, \text{m})}{2 \times 0.5 \, \text{m}} \)
Simplifying this:
\( \lambda_2 = \frac{0.5 \times 10^{-6}}{1} = 0.5 \times 10^{-6} \, \text{m} = 500 \, \text{nm} \)
Since \( 500 \, \text{nm} \) is within the range of 400 nm to 700 nm, this wavelength will have a strong intensity at the hole.

5. Conclusion:
The only wavelength that will have a strong intensity at the hole is \( 500 \, \text{nm} \).

Final Answer:
The wavelength that has a strong intensity at the hole is 500 nm.