A uniform magnetic field existsin region given by →B=3ˆi+4ˆj+5ˆk. A rod of length 5m is placed along y-axis is moved along x- axis with constant speed 1m/sec. Then the magnitude of induced e.m.f in the rod is :
(a) 0
(B) 25V
( c) 20V
(d) 15V
The correct Answer is:B
To find the magnitude of the induced electromotive force (e.m.f) in the rod, we can follow these steps:
Step 1: Identify the Given Values
- Magnetic field →B=3^i+4^j+5^k (in Tesla)
- Length of the rod L=5m (along the y-axis)
- Velocity of the rod →V=1m/s (along the x-axis)
Step 2: Write the Vectors
- The velocity vector of the rod can be expressed as →V=1^im/s.
- The length vector of the rod, which is along the y-axis, can be expressed as →L=5^jm.
Step 3: Use the Formula for Induced EMF
The induced e.m.f E can be calculated using the formula:
E=|→V×→B⋅→L|
Step 4: Calculate the Cross Product →V×→B
To find →V×→B:
→V×→B=(1^i)×(3^i+4^j+5^k)
Using the properties of the cross product:
- ^i×^i=0
- ^i×^j=^k
- ^i×^k=−^j
Calculating the components:
→V×→B=1^i×(3^i)+1^i×(4^j)+1^i×(5^k)
=0+4^k−5^j
So,
→V×→B=−5^j+4^k
Step 5: Calculate the Dot Product with →L
Now, we need to calculate the dot product:
(→V×→B)⋅→L=(−5^j+4^k)⋅(5^j)
Calculating the dot product:
=(−5)(5)+(4)(0)=−25
Step 6: Find the Magnitude of Induced EMF
The magnitude of the induced e.m.f is:
E=|−25|=25V
Conclusion
The magnitude of the induced e.m.f in the rod is 25V.
---
- Magnetic field →B=3^i+4^j+5^k (in Tesla)
- Length of the rod L=5m (along the y-axis)
- Velocity of the rod →V=1m/s (along the x-axis)
- The velocity vector of the rod can be expressed as →V=1^im/s.
- The length vector of the rod, which is along the y-axis, can be expressed as →L=5^jm.
The induced e.m.f E can be calculated using the formula:
E=|→V×→B⋅→L|
To find →V×→B:
→V×→B=(1^i)×(3^i+4^j+5^k)
Using the properties of the cross product:
- ^i×^i=0
- ^i×^j=^k
- ^i×^k=−^j
→V×→B=1^i×(3^i)+1^i×(4^j)+1^i×(5^k)
=0+4^k−5^j
So,
→V×→B=−5^j+4^k
Now, we need to calculate the dot product:
(→V×→B)⋅→L=(−5^j+4^k)⋅(5^j)
Calculating the dot product:
=(−5)(5)+(4)(0)=−25
The magnitude of the induced e.m.f is:
E=|−25|=25V
The magnitude of the induced e.m.f in the rod is 25V.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
The magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
View SolutionWhat is the length of projection of →A=3ˆi+4ˆj+5ˆk on xy plane ?
View SolutionA vector is given by →A=3ˆi+4ˆj+5ˆk. Find the magnitude of →A , unit vector along →A and angles made by →A with coordinate axes.
View SolutionMagnetic force on a charged particle is given by →Fm=q(→v×→B) and electrostatic force →Fe=q→E. A particle having charge q = 1C and mass 1 kg is released from rest at origin. There are electric and magnetic field given by →E=(10ˆi)N/Cforx=1.8m and →B=−(5ˆk)T for 1.8m≤x≤2.4m
A screen is placed parallel to y-z plane at x=3m. Neglect gravity forces.
The speed with which the particle will collide the screen is
View SolutionA uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
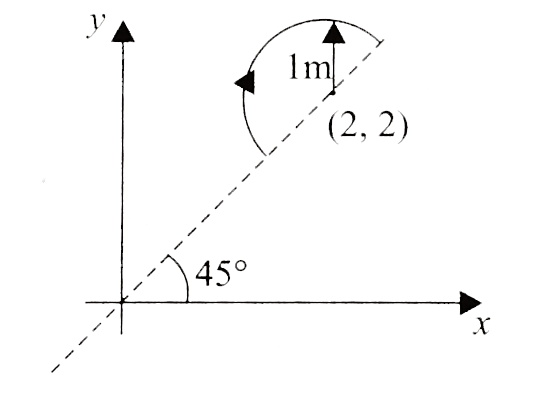
View SolutionA uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
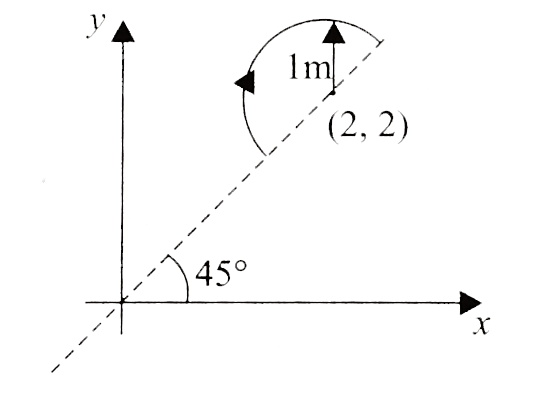
View SolutionThe compenent of →A=ˆi+ˆj+5ˆk perpendicular to →B=3ˆi+4ˆj is
View SolutionA charged particle with charge to mass ratio (qm)=(10)319Ckg−1 enters a uniform magnetic field →B=20ˆi+30ˆj+50ˆkT at time t = 0 with velocity →V=(20ˆi+50ˆj+30ˆk)m/s. Assume that magnetic field exists in large space.
During the further motion of the particle in the magnetic field, the angle between the magnetic field and velocity of the particle
View SolutionA particle is moving with speed 6m/s along the direction of →A=2ˆi+2ˆj−ˆk, then its velocity is :
View SolutionGiven two vectors →A=−ˆi+2ˆj−3ˆk and →B=4ˆi−2ˆj+6ˆk. The angle made by (A+B) with x-axis is :
View Solution
