The magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
v0B0d2a
v0B0d3a
v0B0d22a
0
The correct Answer is:A
To solve the problem of finding the induced EMF in the square loop moving in a magnetic field, we can follow these steps:
1. Understand the Magnetic Field:
The magnetic field is given by:
→B=B0(1+xa)^k
This indicates that the magnetic field varies with the position x.
2. Define the Loop's Position:
The square loop has an edge length d and is placed in the xy-plane, with its edges along the x-axis and y-axis. The loop is moving with a constant velocity →V=V0^i.
3. Calculate the Magnetic Flux:
The magnetic flux Φ through the loop is given by:
Φ=∫→B⋅d→A
For a small strip of the loop of thickness dx at position x, the area dA is d⋅dx (where d is the length of the edge of the square loop). Thus, we can write:
dΦ=B⋅dA=B0(1+xa)d⋅dx
4. Integrate to Find Total Flux:
The total flux through the loop as it moves from x to x+d is:
Φ=∫x+dxB0(1+xa)d⋅dx
This can be simplified as:
Φ=B0d∫x+dx(1+xa)dx
Evaluating this integral gives:
Φ=B0d(x+x22a)x+dx=B0d((x+d+(x+d)22a)−(x+x22a))
5. Differentiate to Find EMF:
According to Faraday's law of electromagnetic induction, the induced EMF (E) is given by:
E=−dΦdt
Since the loop is moving with velocity V0, we can express this as:
E=−dΦdx⋅dxdt=−dΦdx⋅V0
6. Calculate the Derivative of Flux:
After calculating the flux, we differentiate it with respect to x and multiply by V0 to find the induced EMF:
E=B0d⋅ddx(d22a+d)⋅V0
7. Final Result:
After performing the calculations, we find:
E=B0d2V0a
Final Answer:
The induced EMF in the loop is:
E=B0d2V0a
The magnetic field is given by:
→B=B0(1+xa)^k
This indicates that the magnetic field varies with the position x.
The square loop has an edge length d and is placed in the xy-plane, with its edges along the x-axis and y-axis. The loop is moving with a constant velocity →V=V0^i.
The magnetic flux Φ through the loop is given by:
Φ=∫→B⋅d→A
For a small strip of the loop of thickness dx at position x, the area dA is d⋅dx (where d is the length of the edge of the square loop). Thus, we can write:
dΦ=B⋅dA=B0(1+xa)d⋅dx
The total flux through the loop as it moves from x to x+d is:
Φ=∫x+dxB0(1+xa)d⋅dx
This can be simplified as:
Φ=B0d∫x+dx(1+xa)dx
Evaluating this integral gives:
Φ=B0d(x+x22a)x+dx=B0d((x+d+(x+d)22a)−(x+x22a))
According to Faraday's law of electromagnetic induction, the induced EMF (E) is given by:
E=−dΦdt
Since the loop is moving with velocity V0, we can express this as:
E=−dΦdx⋅dxdt=−dΦdx⋅V0
After calculating the flux, we differentiate it with respect to x and multiply by V0 to find the induced EMF:
E=B0d⋅ddx(d22a+d)⋅V0
After performing the calculations, we find:
E=B0d2V0a
The induced EMF in the loop is:
E=B0d2V0a
Topper's Solved these Questions
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:PHYSICS
Explore 17 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:MATHS
Explore 14 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:part-2 physics
Explore 71 Videos
- TEST PAPER 4Book:ALLENChapter:TEST PAPER 4Exercise:PHYSICS
Explore 44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
The magnetic field I nan reigion is given by B=B0XaK. A Squrae edges along the x and y axis. The loop is moved with a constant velocity . The emf induced in the loop is

View SolutionThe magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View SolutionThe magnetic field existing in a region is gicen by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View SolutionThe magnetic field existing in a region is given by ,B=B0(xL+x2L2)ˆk.A square loop edge L carrying a current I is placed with its parallel to the X and Y-axis Find the net magnetic force experienced by the loop
View SolutionA uniform magnetic field existsin region given by →B=3ˆi+4ˆj+5ˆk. A rod of length 5m is placed along y-axis is moved along x- axis with constant speed 1m/sec. Then the magnitude of induced e.m.f in the rod is :
View SolutionA uniform magnetic field existsin region given by →B=3ˆi+4ˆj+5ˆk. A rod of length 5m is placed along y-axis is moved along x- axis with constant speed 1m/sec. Then the magnitude of induced e.m.f in the rod is :
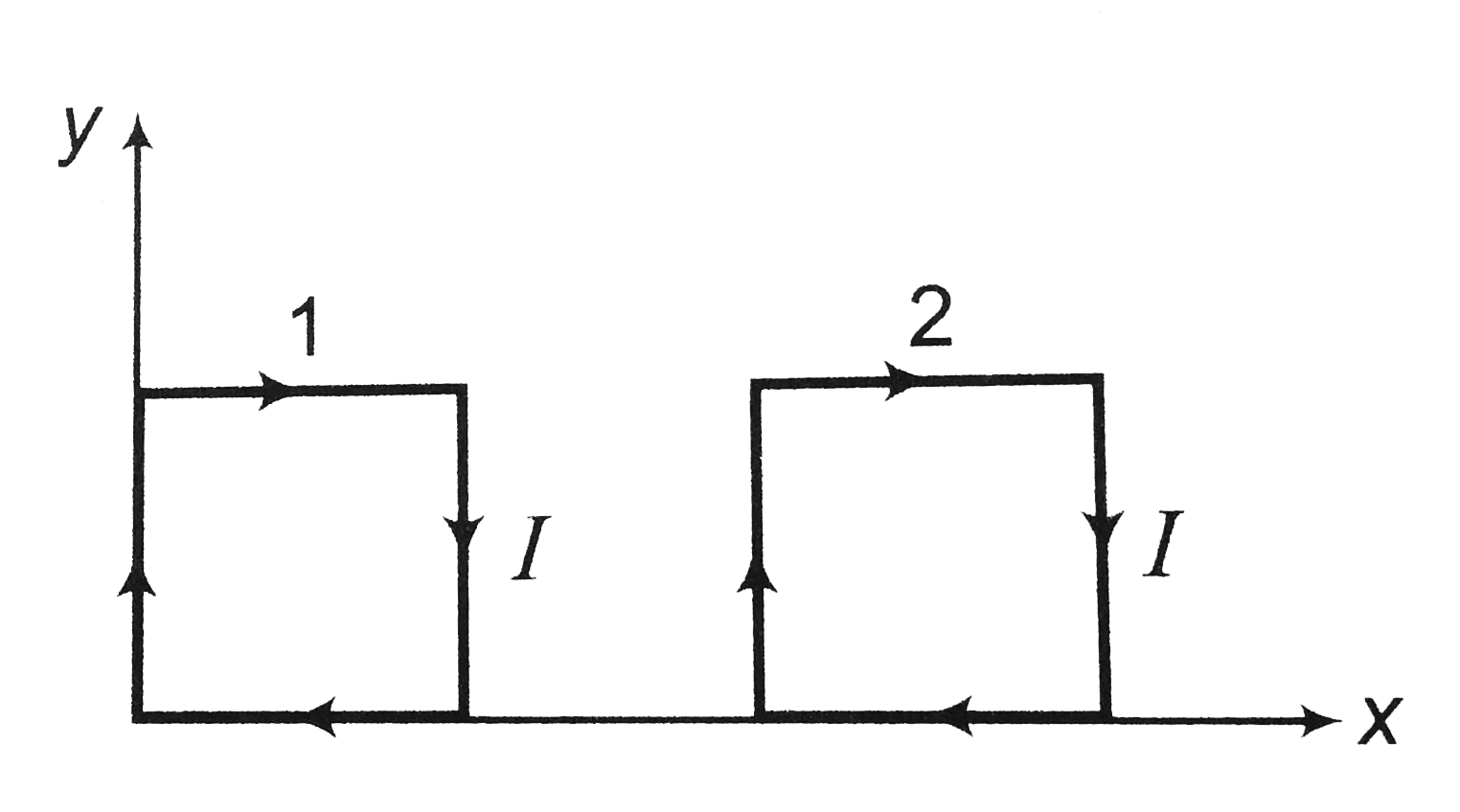
View SolutionMagnetic field in a region is given by B=B0xˆk. Two loops each of side a is placed in the magnetic region in the xy-plane with one of its sides on x-axis. If F1 is the force on loop 1 and dF2 be the force on loop 2, then
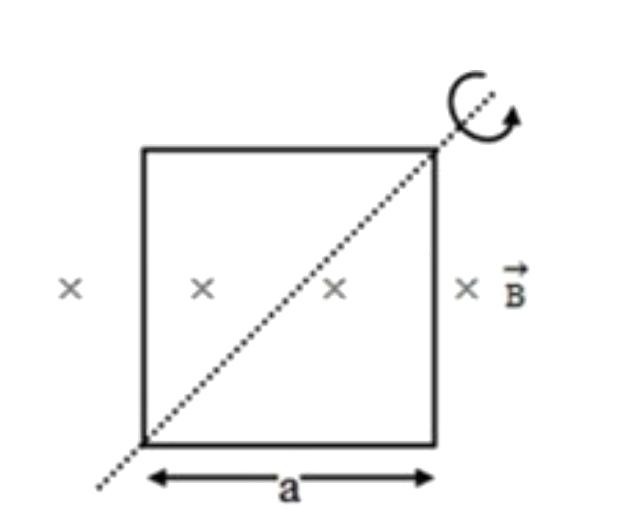
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View SolutionIn the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is
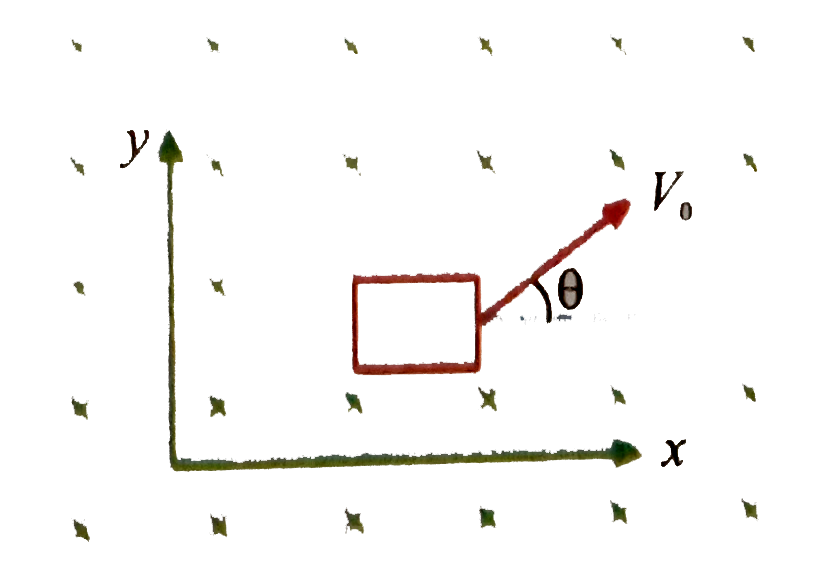
View SolutionIn the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is

View Solution

