A ring of mass 'm' and radius 'r' carrying current i0 is lying in the X-Y plane with centre at origin. A uniform magnetic field of strength B=B0(2ˆi−3ˆj+5ˆk)T is applied in the region. If the ring rotates about the axid initial magnetic energy stored in the ring will be. (In joules)
−π2i0B0
−5πr2i0B0
−3πr2i0B0
−2πr2i0B0
The correct Answer is:B
To solve the problem, we need to calculate the initial magnetic energy stored in the ring that is carrying a current and is placed in a uniform magnetic field. Here are the steps to arrive at the solution:
1. Identify the Magnetic Moment (μ):
The magnetic moment (μ) of a current-carrying loop is given by the formula:
μ=I⋅A
where I is the current flowing through the loop and A is the area of the loop. For a ring of radius r:
A=πr2
Therefore, the magnetic moment of the ring is:
μ=I0⋅πr2
The direction of the magnetic moment will be along the z-axis (k direction) since the ring lies in the XY plane.
2. Given Magnetic Field (B):
The magnetic field is given as:
B=B0(2^i−3^j+5^k)T
3. Calculate the Magnetic Energy (U):
The magnetic energy stored in a magnetic moment in a magnetic field is given by the formula:
U=−μ⋅B
Substituting the values we have:
U=−(I0⋅πr2^k)⋅(B0(2^i−3^j+5^k))
4. Evaluate the Dot Product:
The dot product can be calculated as follows:
μ⋅B=(I0⋅πr2)⋅B0⋅5
Since the only component that contributes to the dot product is along the k direction:
μ⋅B=I0⋅πr2⋅5B0
5. Final Expression for Magnetic Energy:
Thus, the magnetic energy stored in the ring is:
U=−5I0πr2B0
Final Answer:
The initial magnetic energy stored in the ring is:
U=−5πr2I0B0Joules
The magnetic moment (μ) of a current-carrying loop is given by the formula:
μ=I⋅A
where I is the current flowing through the loop and A is the area of the loop. For a ring of radius r:
A=πr2
Therefore, the magnetic moment of the ring is:
μ=I0⋅πr2
The direction of the magnetic moment will be along the z-axis (k direction) since the ring lies in the XY plane.
The magnetic field is given as:
B=B0(2^i−3^j+5^k)T
The magnetic energy stored in a magnetic moment in a magnetic field is given by the formula:
U=−μ⋅B
Substituting the values we have:
U=−(I0⋅πr2^k)⋅(B0(2^i−3^j+5^k))
The dot product can be calculated as follows:
μ⋅B=(I0⋅πr2)⋅B0⋅5
Since the only component that contributes to the dot product is along the k direction:
μ⋅B=I0⋅πr2⋅5B0
Thus, the magnetic energy stored in the ring is:
U=−5I0πr2B0
The initial magnetic energy stored in the ring is:
U=−5πr2I0B0Joules
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
17 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
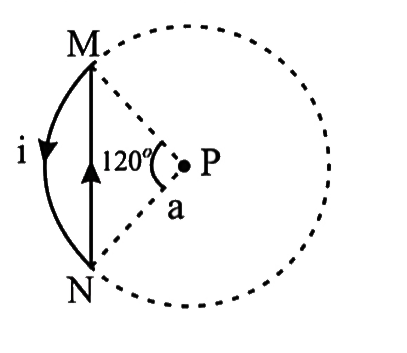
A wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
View SolutionA ring of radius 5 m is lying in the x-y plane and is carrying current of 1 A in anticlockwise sense. If a uniform magnetic field −B=3ˆi+4ˆj is switched on, then the coordinates of point about which the loop will lift up is:

View SolutionA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
View Solution(a) Write the expression for the equivalent megnetic moment of a planer current loop of area A, having N turns and carrying a current i. Use the expression to find the magentic dipole moment of a revolving electron ?
(b) A circuit loop of radius r, having N turns and carrying current I, is kept in the XY plane. It is then subjected to a uniform magnetic field →B=Bxˆi+Byˆj+Bzˆk . Obtain expression for the magnetic potential energy of the coil-magnetic field system.
View SolutionA circular current carrying loop is placed in x-y plane as shown in figure. A uniform magnetic field B=B0ˆK is present in the region. Match the following.


View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
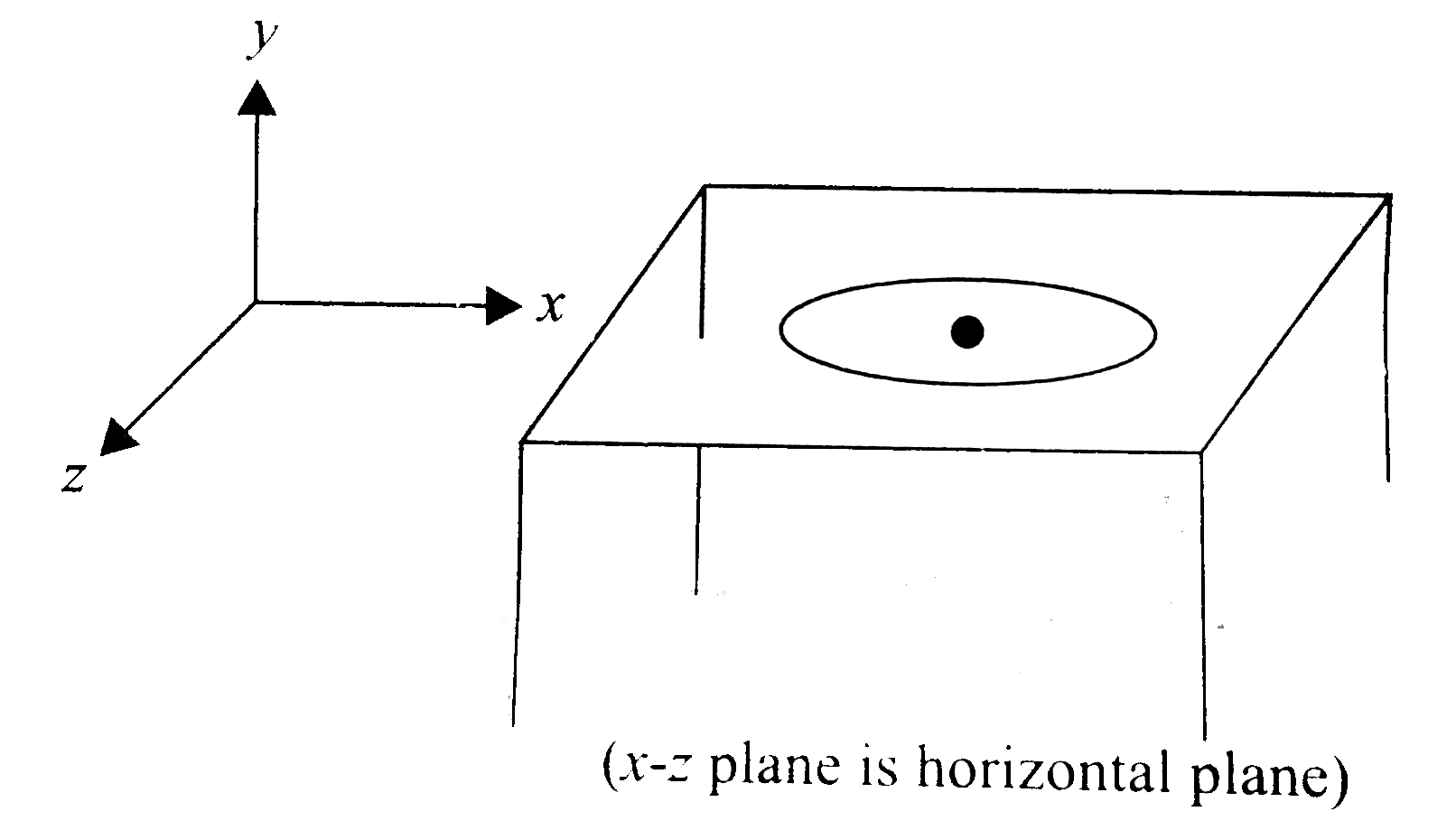
Heat generated (in kJ) through the ring till the instant when ring start toppling is
View SolutionA ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will

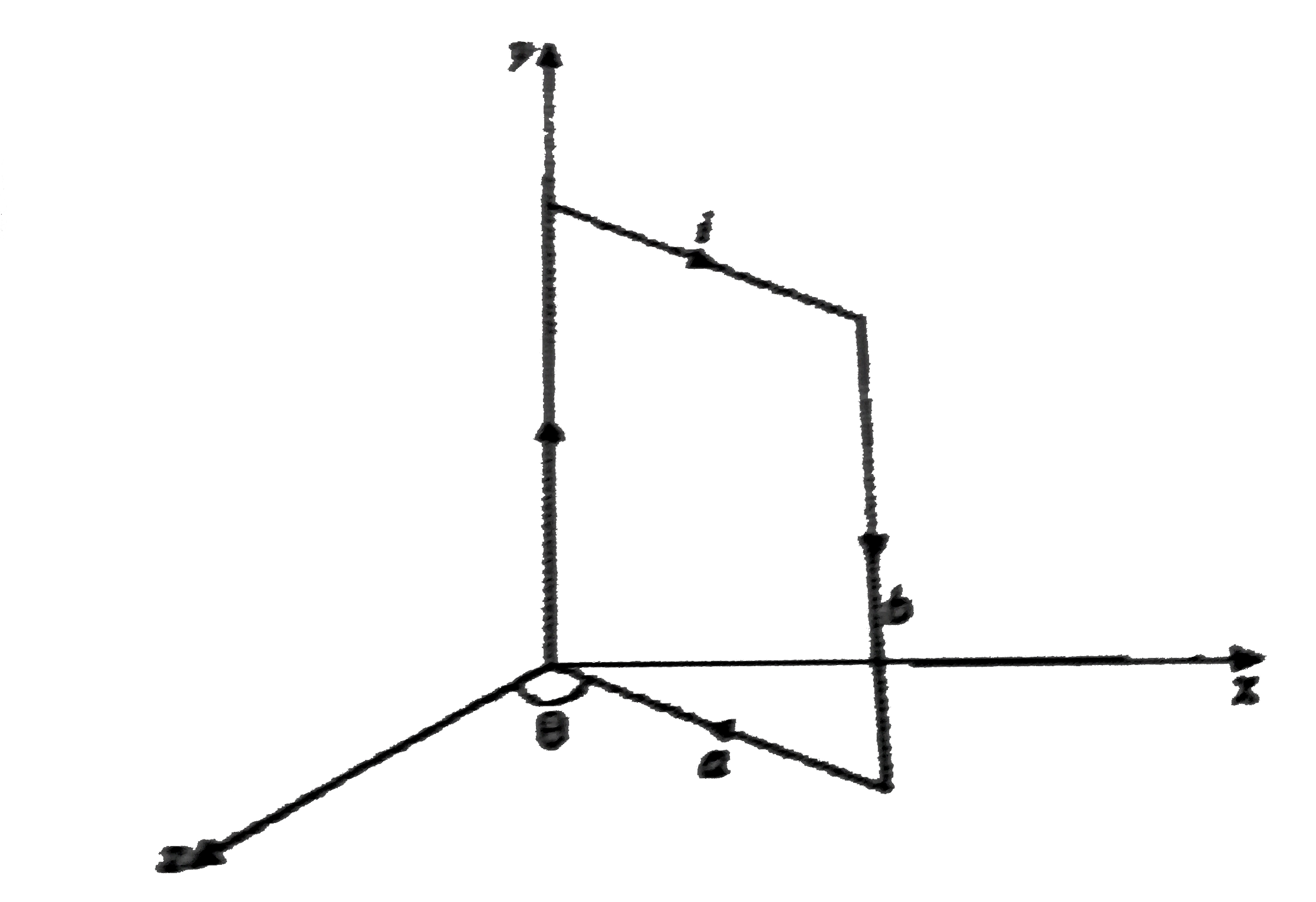
View SolutionA rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
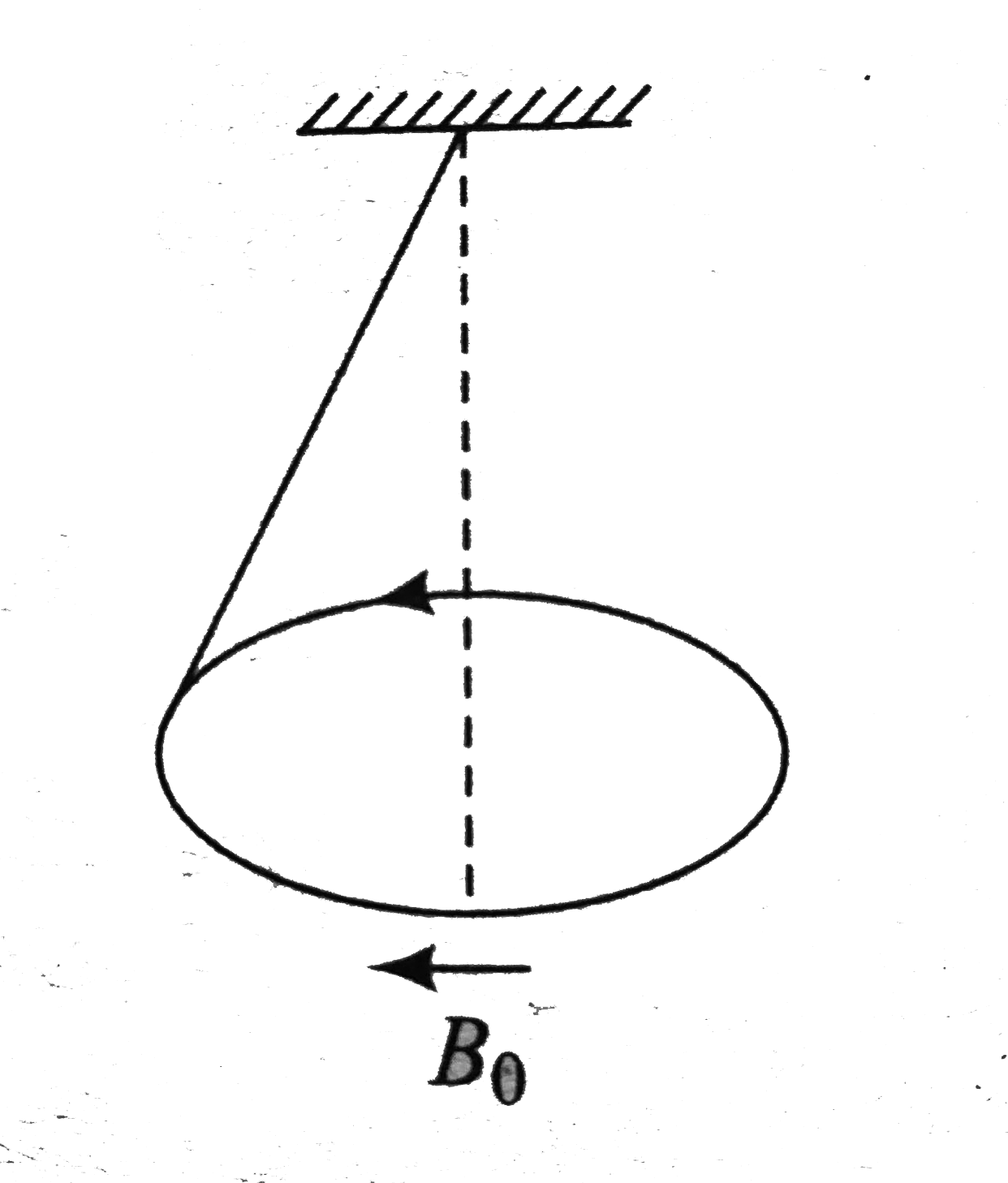
View SolutionA uniform current carrying ring of mass m and radius R is connected by a massless string as shown in Fig. 1.142. A uniform magnetic field B0 exists in the region to keep the ring in horizontal position, then the current in the ring is (l=length of string)
 .
.
View Solution
