Find force F required to keep the system in equilibrium. The dimensions of the system are d=0.3m and a=0.2m. Assume the rods to be massless.

150ˆi
150(−ˆk)
150(−ˆi)
It cannot be in equilibrium
The correct Answer is:A
ˆτc=−dˆi×100ˆj+(−aˆj)×(+Fˆi)=0
−100dˆk+aFˆk=0
⇒100d=aF⇒F=100×0.30.2=150
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
17 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
For a system in equilibrium, ΔG=0, under conditions of constant
View SolutionIf system is in equilibrium then find relation between m1 and m2
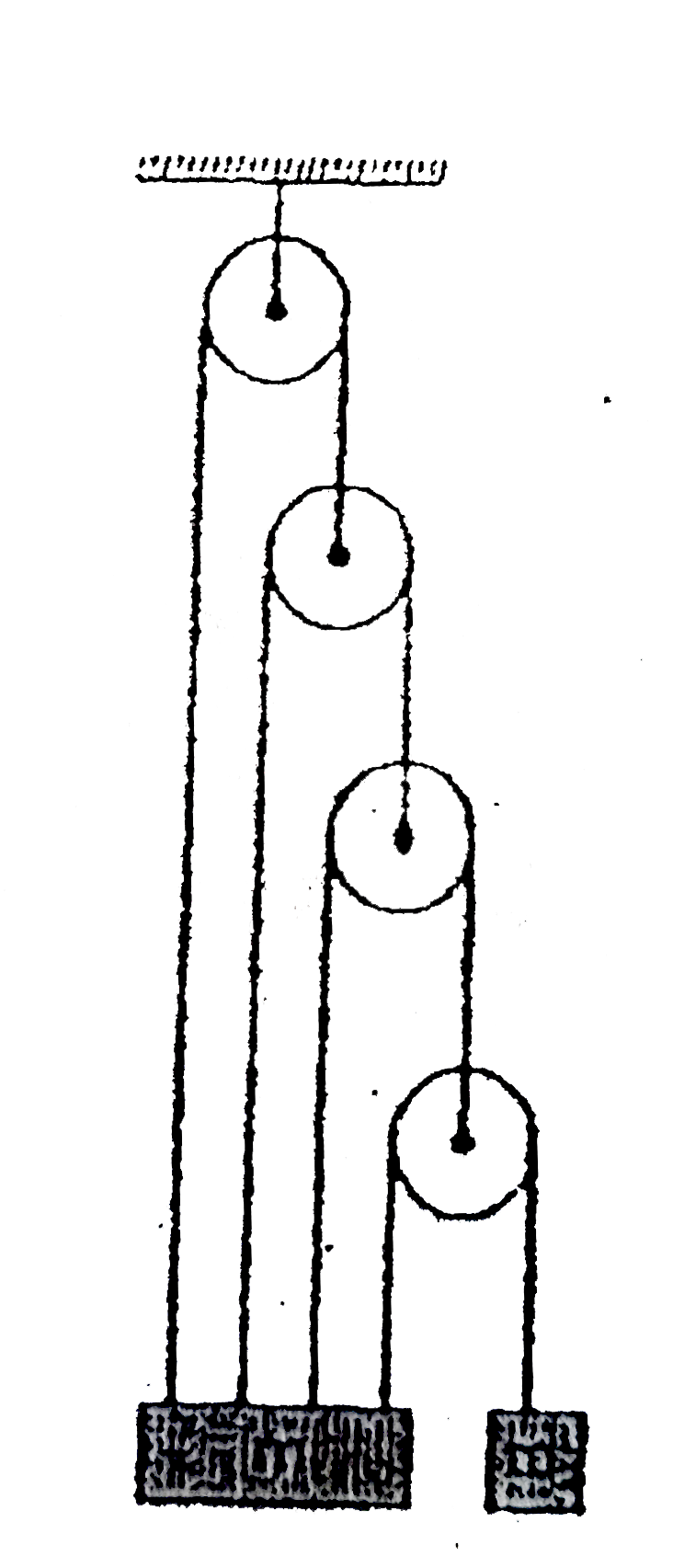
View SolutionFind m3 if the system is in equilibrium the incline is smooth and string and pulley are light
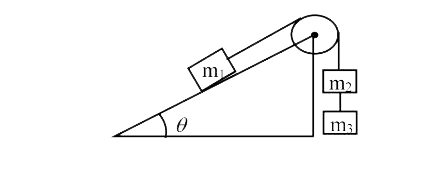
View SolutionFor equilibrium of the system, value of mass m should be

View SolutionFor the equilibrium of the system shown, the value of mass m should be
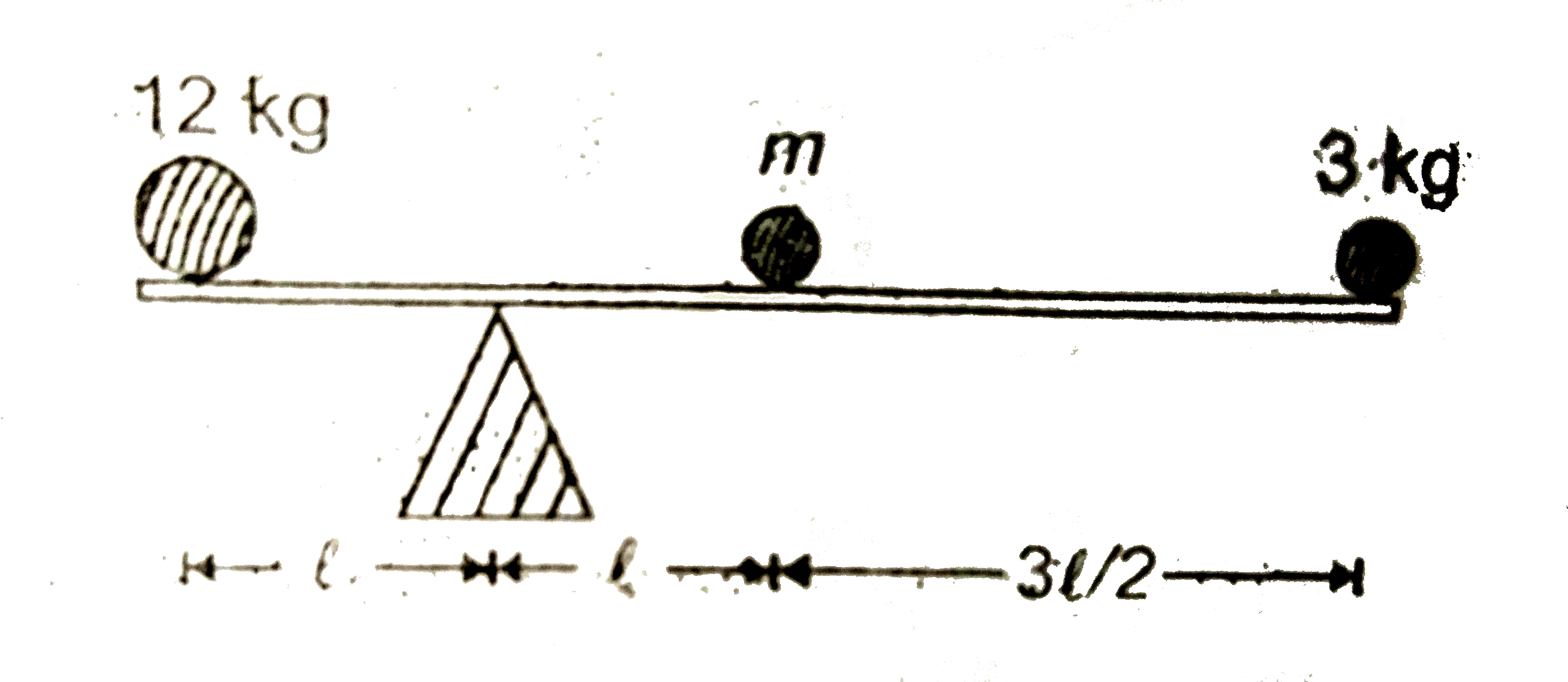
View SolutionFor the system shown in figure , to be in equilibrium , determine mass m .
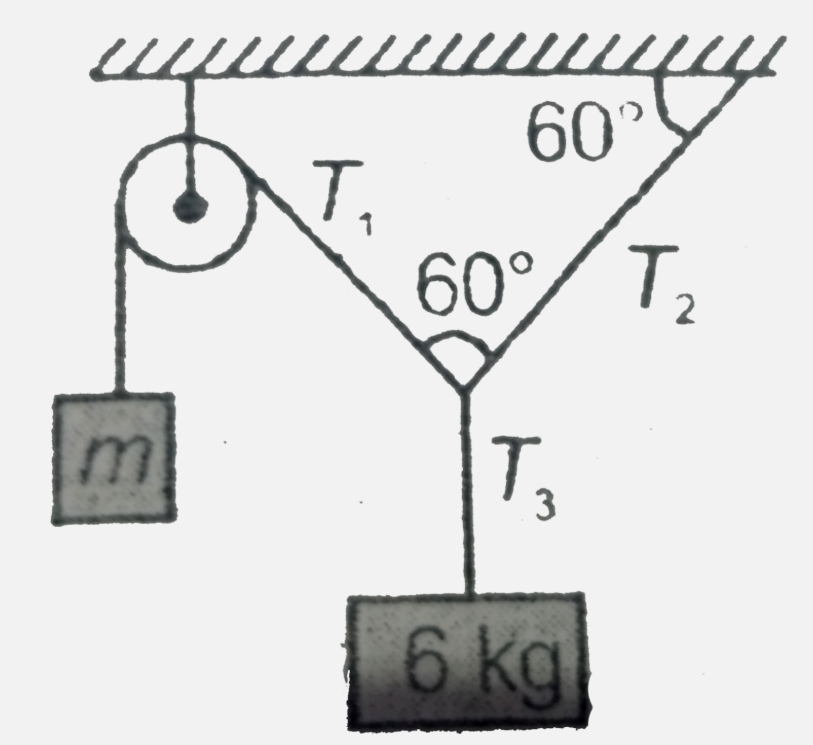
View SolutionA mass of 0.5 kg is hung from a spring. A gradually increasing 0.5 N force is required to pull the mass downward a distance of 0.25 m from its equilibrium position,if the mass is then released from this position, find
(a) The total energy of the system .
(b) The frequency of the oscillation
(c ) The speed and acceleration of the mass as it passes the equilibrium position.
(d) The speed and acceleration of the mass when the diplacement from equilibrium is 0.25 m
(e) For the initial condition stated, write down the diplacement equation of motion for this mass.
View SolutionFind the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View Solution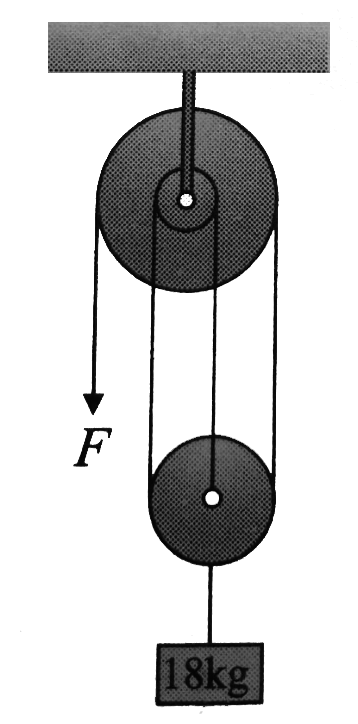
In the figure, at the free end of the light string, a force F is supplied to keep the suspended mass of 18 kg at rest. Then the force exerted by the ceiling on the system (assume that the string segments are vertical and the pulleys are light and smooth) is:(g=10ms2)
View SolutionFind the value of tension in string 1 if the system equilibrium ? (g=10 m/s2)
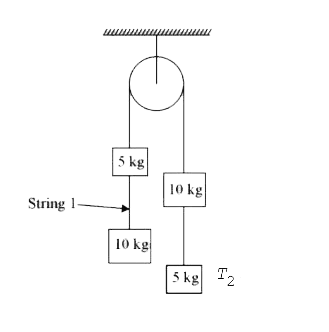
View Solution
