A magnetic field induction is changing in magnitude in a region at a constant rate dB/dt. A given mass m of copper drawn into a wire and formed into a loop is placed perpendicular to the field. If the values of specific resistance and density of copper are ρ and σ respectively, then the current in the loop is given by :
(a) m2πρddBdt
(b) m4πa2rdBdt
(c) m4πaddBdt
(d) m4πρddBdt
The correct Answer is:D
To solve the problem, we need to determine the current in a loop made from a given mass of copper when placed in a changing magnetic field. Here’s the step-by-step solution:
Step 1: Understand the given parameters
We have:
- A magnetic field induction changing at a rate of dBdt.
- A mass m of copper.
- The specific resistance (resistivity) of copper denoted as ρ.
- The density of copper denoted as σ.
Step 2: Relate mass to volume
The mass of the copper wire can be expressed in terms of its volume and density:
m=σ⋅V
where V is the volume of the wire.
Step 3: Express volume in terms of cross-sectional area and length
The volume V of the wire can also be expressed as:
V=A⋅L
where A is the cross-sectional area and L is the length of the wire.
Step 4: Relate mass to length
Substituting the volume expression into the mass equation gives:
m=σ⋅A⋅L
From this, we can express the length L of the wire as:
L=mσ⋅A
Step 5: Determine the induced EMF
The induced EMF E in the loop due to the changing magnetic field is given by:
E=−dΦdt
For a loop of area A in a magnetic field B, the magnetic flux Φ is:
Φ=B⋅A
Thus,
E=A⋅dBdt
Step 6: Calculate the area of the loop
If we assume the loop is circular, the area A can be expressed in terms of the radius r:
A=πr2
Since the length of the wire L is the circumference of the loop:
L=2πr⟹r=L2π
Substituting this into the area formula gives:
A=π(L2π)2=L24π
Step 7: Substitute area into EMF formula
Now substituting A back into the EMF equation:
E=L24π⋅dBdt
Step 8: Calculate the resistance of the loop
The resistance R of the wire is given by:
R=ρ⋅LA
Substituting for A:
R=ρ⋅LL24π=4πρL
Step 9: Calculate the current using Ohm's Law
Using Ohm's Law, the current I is given by:
I=ER
Substituting the expressions for E and R:
I=L24π⋅dBdt4πρL=L316π2ρ⋅dBdt
Step 10: Substitute L in terms of mass and density
From earlier, we have L=mσA. Substitute this into the current equation:
I=(mσA)316π2ρ⋅dBdt
Final Step: Simplify the expression
After simplification, we arrive at the final expression for the current I:
I=m4πσρ⋅dBdt
Conclusion
Thus, the current in the loop is given by:
I=m4πσρ⋅dBdt
We have:
- A magnetic field induction changing at a rate of dBdt.
- A mass m of copper.
- The specific resistance (resistivity) of copper denoted as ρ.
- The density of copper denoted as σ.
The mass of the copper wire can be expressed in terms of its volume and density:
m=σ⋅V
where V is the volume of the wire.
The volume V of the wire can also be expressed as:
V=A⋅L
where A is the cross-sectional area and L is the length of the wire.
Substituting the volume expression into the mass equation gives:
m=σ⋅A⋅L
From this, we can express the length L of the wire as:
L=mσ⋅A
The induced EMF E in the loop due to the changing magnetic field is given by:
E=−dΦdt
For a loop of area A in a magnetic field B, the magnetic flux Φ is:
Φ=B⋅A
Thus,
E=A⋅dBdt
If we assume the loop is circular, the area A can be expressed in terms of the radius r:
A=πr2
Since the length of the wire L is the circumference of the loop:
L=2πr⟹r=L2π
Substituting this into the area formula gives:
A=π(L2π)2=L24π
Now substituting A back into the EMF equation:
E=L24π⋅dBdt
The resistance R of the wire is given by:
R=ρ⋅LA
Substituting for A:
R=ρ⋅LL24π=4πρL
Using Ohm's Law, the current I is given by:
I=ER
Substituting the expressions for E and R:
I=L24π⋅dBdt4πρL=L316π2ρ⋅dBdt
From earlier, we have L=mσA. Substitute this into the current equation:
I=(mσA)316π2ρ⋅dBdt
After simplification, we arrive at the final expression for the current I:
I=m4πσρ⋅dBdt
Thus, the current in the loop is given by:
I=m4πσρ⋅dBdt
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Multiple Correct
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Asserton - Reasoning
Explore 8 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Subjective
Explore 13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
Similar Questions
A magnetic field induction is changing in magnitude at a constant rate dB/dt . A given mass m of copper is drawn into a wire of radius α and formed into a loop of radius r is placed perpendicular to the field. Show that induced current in the loop is given by i=m4πpδdBdt
p : resistivity, δ : density of copper.
View SolutionA rectangular copper coil is placed in a uniform magnetic field of induction 40 mT with its plane perpendicular to the field. The area of the coil is shrinking at a constant rate of 0.5m2s−1. The emf induced in the coil is
View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :
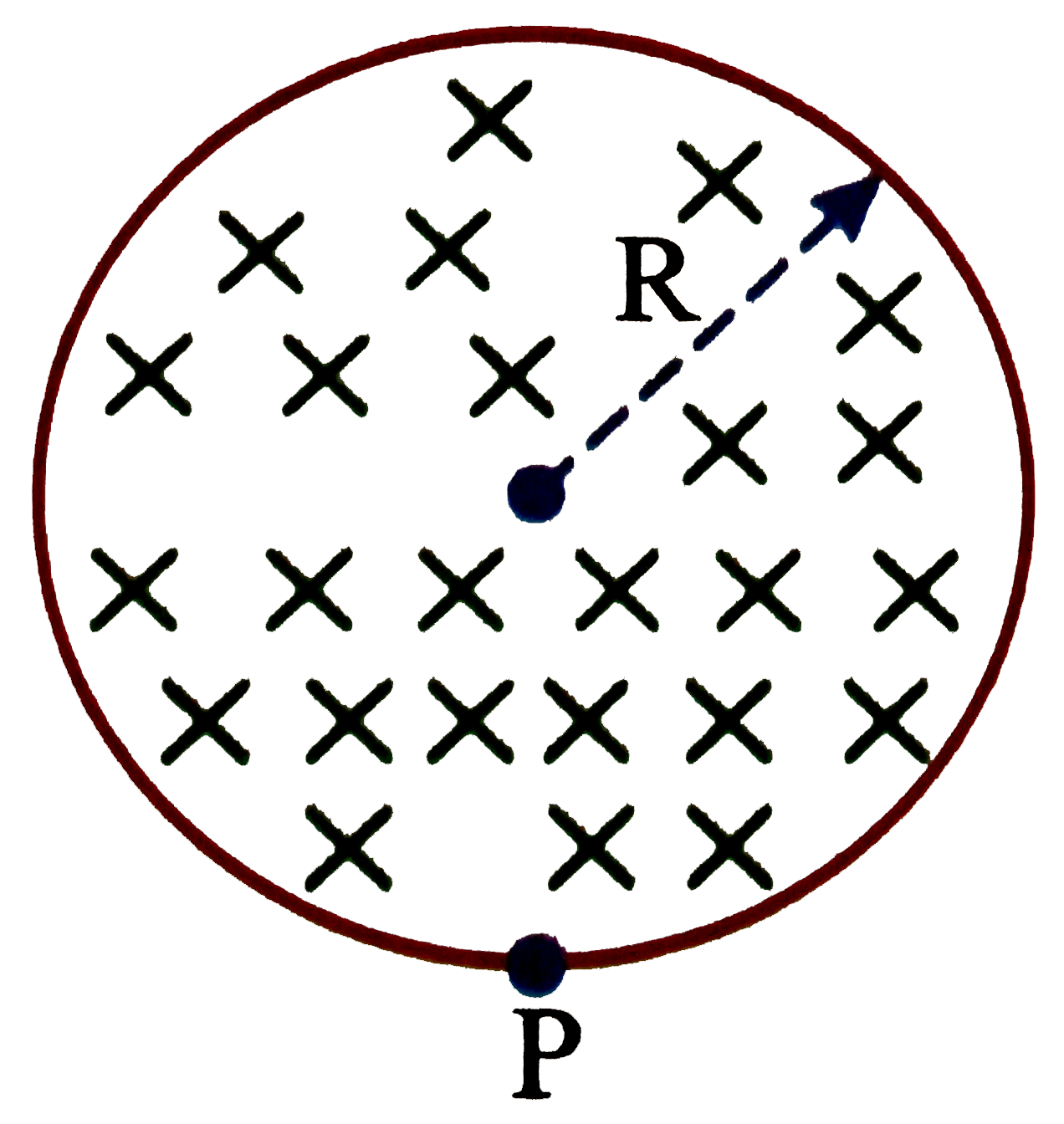
View SolutionA uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :

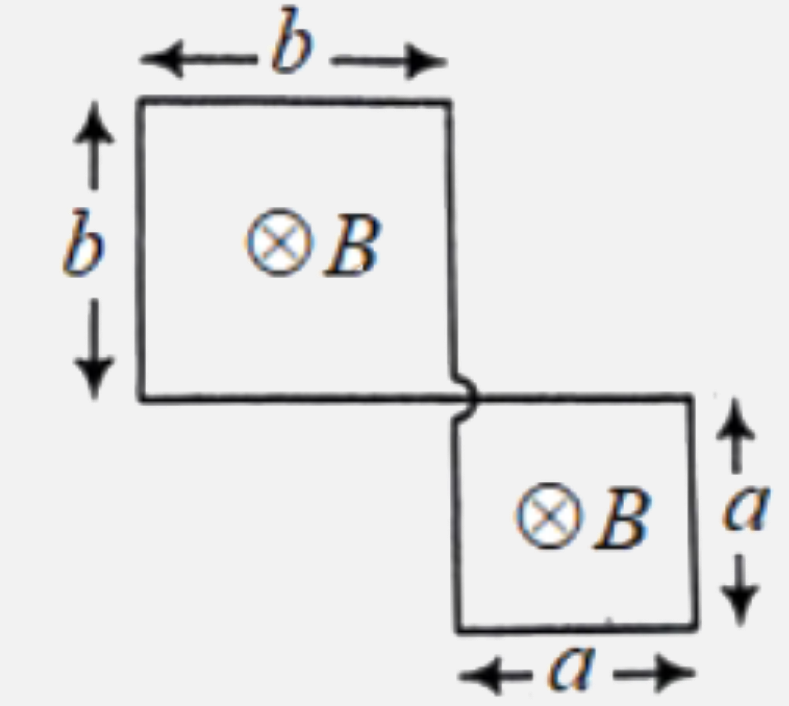
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is a constant and t is time. The induced current flowing through loop is
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is

View SolutionA circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.
View SolutionA loop of Irregular shape made of flexible conducting wire carrying clockwise current is placed in uniform inward magnetic field, such that its plane is perpendicular to the field. Then the loop
View Solution