A circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.
The correct Answer is:A, B, C
Let's solve the problem step by step.
Given:
- Radius of the circular loop, r=1m
- Magnetic field, B(t)=6tT (where t is time in seconds)
- Resistance of the loop, R=1Ω/m
(a) Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
Step 1: Calculate the area of the circular loop.
A=πr2=π(1)2=πm2
Step 2: Find the rate of change of the magnetic field, dBdt.
dBdt=d(6t)dt=6T/s
Step 3: Use Faraday's law of electromagnetic induction to find the induced emf (E).
E=−AdBdt=−π⋅6=−6πV
(Note: The negative sign indicates the direction of induced emf according to Lenz's law, but we can consider the magnitude for this problem.)
Result:
E=6πV
(b) Find the electric field in the tangential direction, induced due to the changing magnetic field.
Step 1: Use the relationship between the induced emf and the electric field.
E=E⋅2πr
Step 2: Substitute the values to find the electric field E.
E⋅2π(1)=6π
E=6π2π=3V/m
Result:
E=3V/m
(c) Find the current in the loop if its resistance is 1Ω/m.
Step 1: Calculate the total resistance of the loop.
Since the resistance is given per meter and the circumference of the loop is 2πr:
R=1Ω/m×2π(1)=2πΩ
Step 2: Use Ohm's law to find the current I.
I=ER=6π2π=3A
Result:
I=3A
Summary of Results:
- (a) Induced emf, E=6πV
- (b) Electric field, E=3V/m
- (c) Current, I=3A
- Radius of the circular loop, r=1m
- Magnetic field, B(t)=6tT (where t is time in seconds)
- Resistance of the loop, R=1Ω/m
A=πr2=π(1)2=πm2
dBdt=d(6t)dt=6T/s
E=−AdBdt=−π⋅6=−6πV
(Note: The negative sign indicates the direction of induced emf according to Lenz's law, but we can consider the magnitude for this problem.)
E=6πV
E=E⋅2πr
E⋅2π(1)=6π
E=6π2π=3V/m
E=3V/m
Since the resistance is given per meter and the circumference of the loop is 2πr:
R=1Ω/m×2π(1)=2πΩ
I=ER=6π2π=3A
I=3A
- (a) Induced emf, E=6πV
- (b) Electric field, E=3V/m
- (c) Current, I=3A
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
Electric field induced by changing magnetic fields are
View SolutionFind the emf induced in the coil shown in figure.The magnetic field is perpendicular to the plane of the coil and is constant.
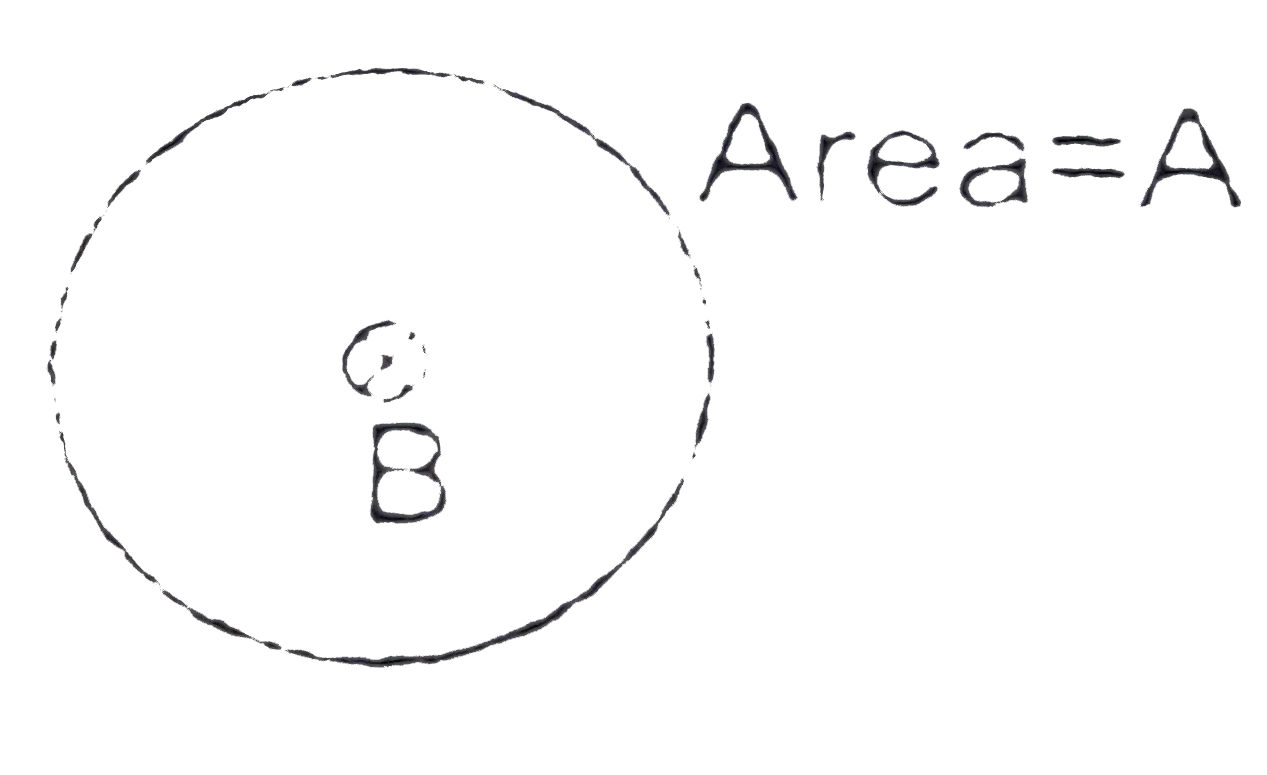
View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionA coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is :
View SolutionA rectangular loop of area 0.06 m2 is placed in a magnetic field of 0.3T with its plane inclined 30∘ to the field. Find the flux linked with the coil .
View SolutionFind the direction of induced current in the coil shown in figure.Magnetic field is perpendicular to the plane of coil and it is increasing with time.
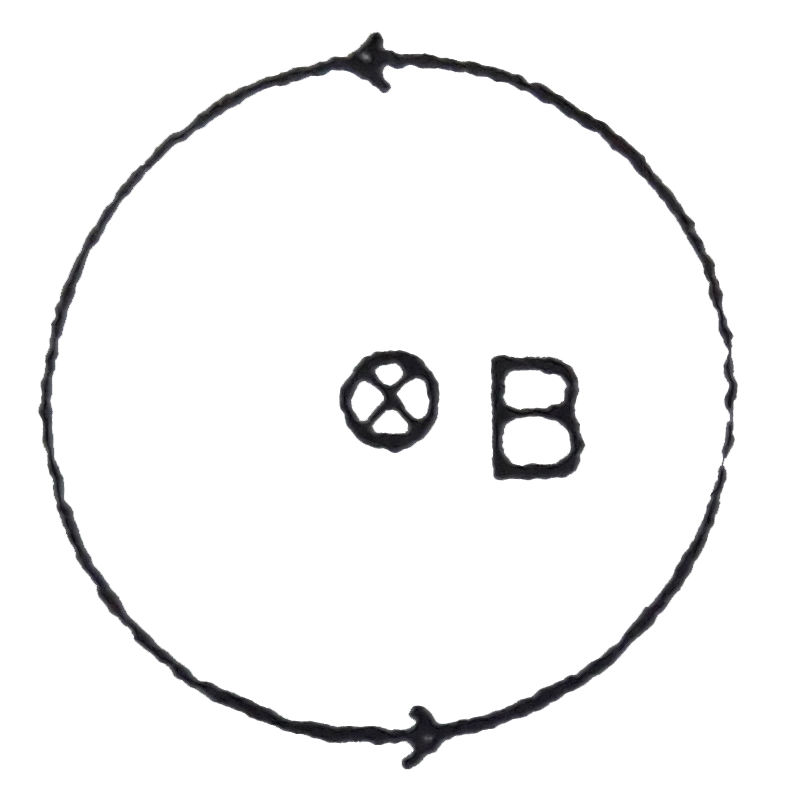
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View SolutionA coil is placed in a constant magnetic field. The magnetic field is parallel to the plane of the coil as shown in Fig. 3.28. Find the emf induced in the coil if B increasing.

View SolutionA triangular loop is placed in a dot ⊙ magnetic field as shown in figure. Find the direction of induced current in the loop if magnetic field is increasing.
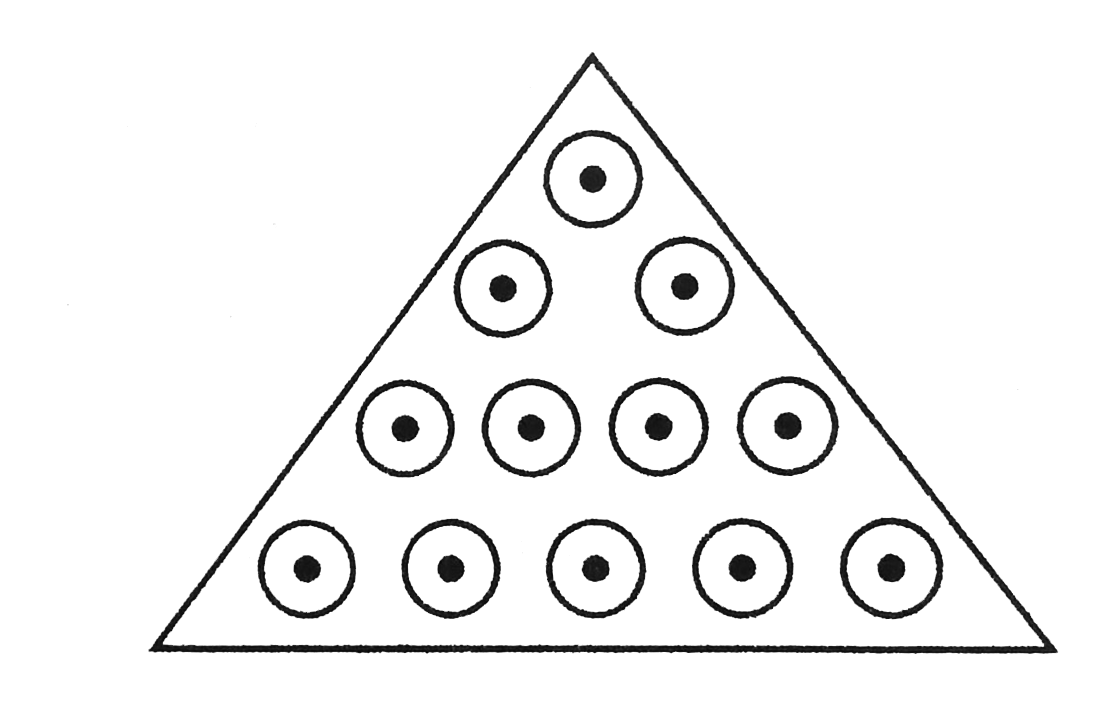
View SolutionA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in time interval t. The emf induced in the coil will be
View Solution
