Calculate the magnetic moment (in Am2 ) of a thin wire with a current I = 8A, wound tightly on half a torus (see figure). The diameter of the cross section of the torus is equal to d = 5 cm, and the number of turns is N = 500.

The correct Answer is:12A.m2
M=π∫θ=0dMsinθ
=π∫θ=0(dN).i.A.sinθ=π∫0Nπ⊥(pd24)sinθdθ
M=12N.i.d2⇒M=12(Ampm2)

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-3
29 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Calculating the magnetic moment ( in Am2) of a thin wire with a current I=8A, wound tightlly on a half a tore (see figure). The diameter of the cross section of the tore is equal to d=5cm, and the number of turns is N=500.
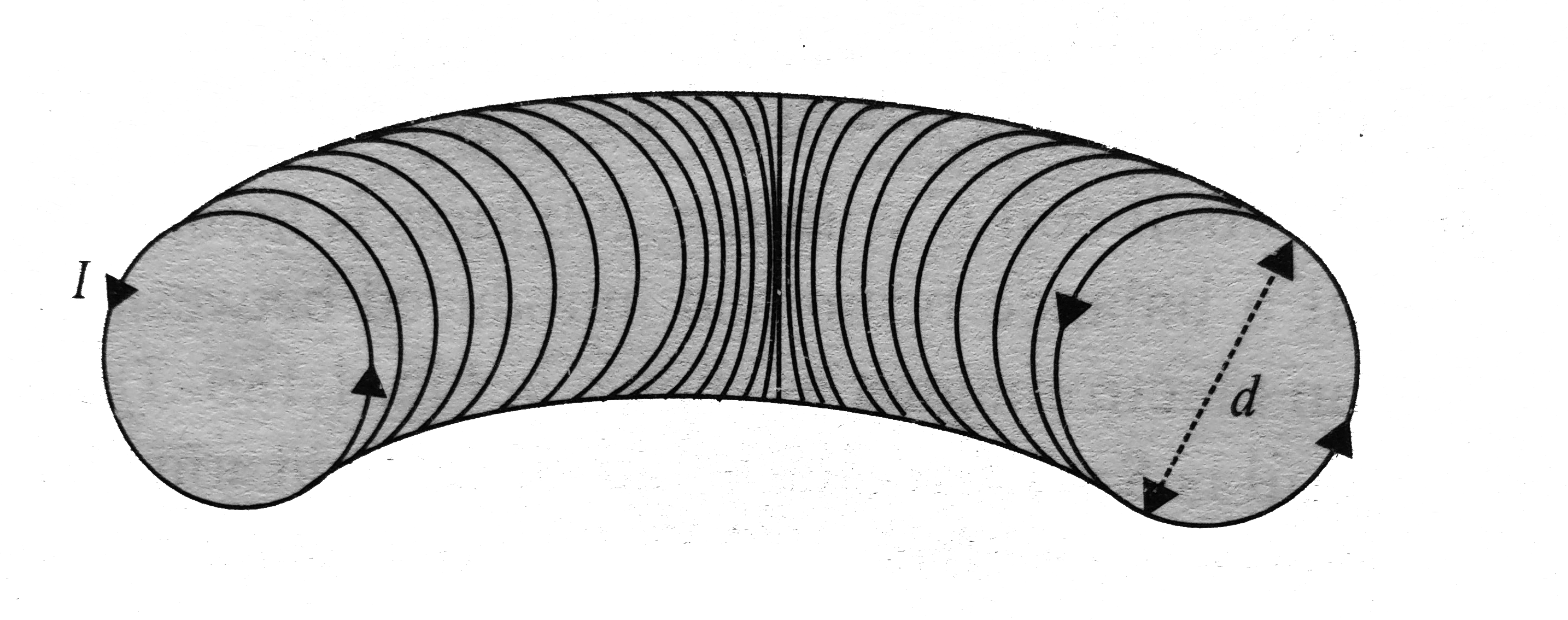
View SolutionCalculating the magnetic moment ( in Am2) of a thin wire with a current I=0.8A, wound tightlly on a half a tore (see figure). The diameter of the cross section of the tore is equal to d=5cm, and the number of turns is N=500.

View Solution
Knowledge Check
A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.A2πλ2I0ln(as)sin(2πυt)ˆkB1λ2I0ln(as)sin(2πυt)ˆkCπλ2I0ln(as)sin(2πυt)ˆkDZeroA closely wound solenoid of 750 turns and area of cross section of 5×104m2 carries a current of 3.0 A. Its associated magnetic moment is
A4.12JT−1B3.12JT−1C2.12JT−1D1.13JT−1
A small coil is introduced between the poles of an electromagnet so that its axis coincides with the magnetic field direction. The cross-sectional area of the coil is equal to S=3.0mm2, the number of turns is N=60. When the coil turns through 180∘ about its diameter, a galvanometer connected to the coil indicates a charge q=4.5μC flowing through it. Find the magnetic induction magnitude between the poles, provided the total resistance of the electric circuit equals R=40Ω.
View SolutionFind the magnetic induction of the field at the point O at a loop with current I, whose shape is illustrated in figure
(a)In figure a the radii a and b, as well as the angle φ are known
(b)In figure b,the raidus a and the side b are known.
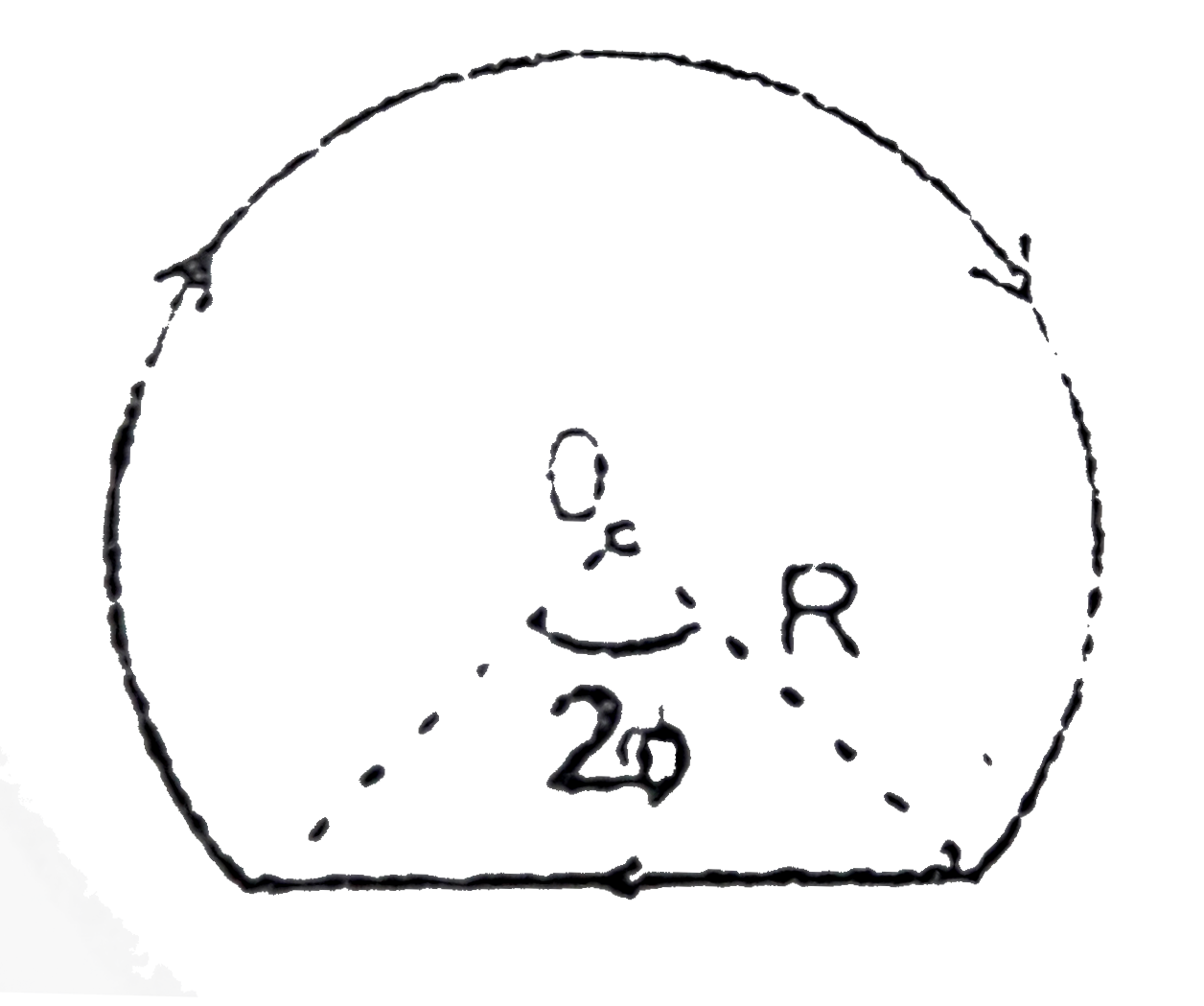
(c)A current I=5.0A flows along a thin wire shaped as shown in figure.The radius of a curved part of the wire is equal to R=120mm,the angle 2φ=90∘.Find the magnetic induction of the field at the point O.
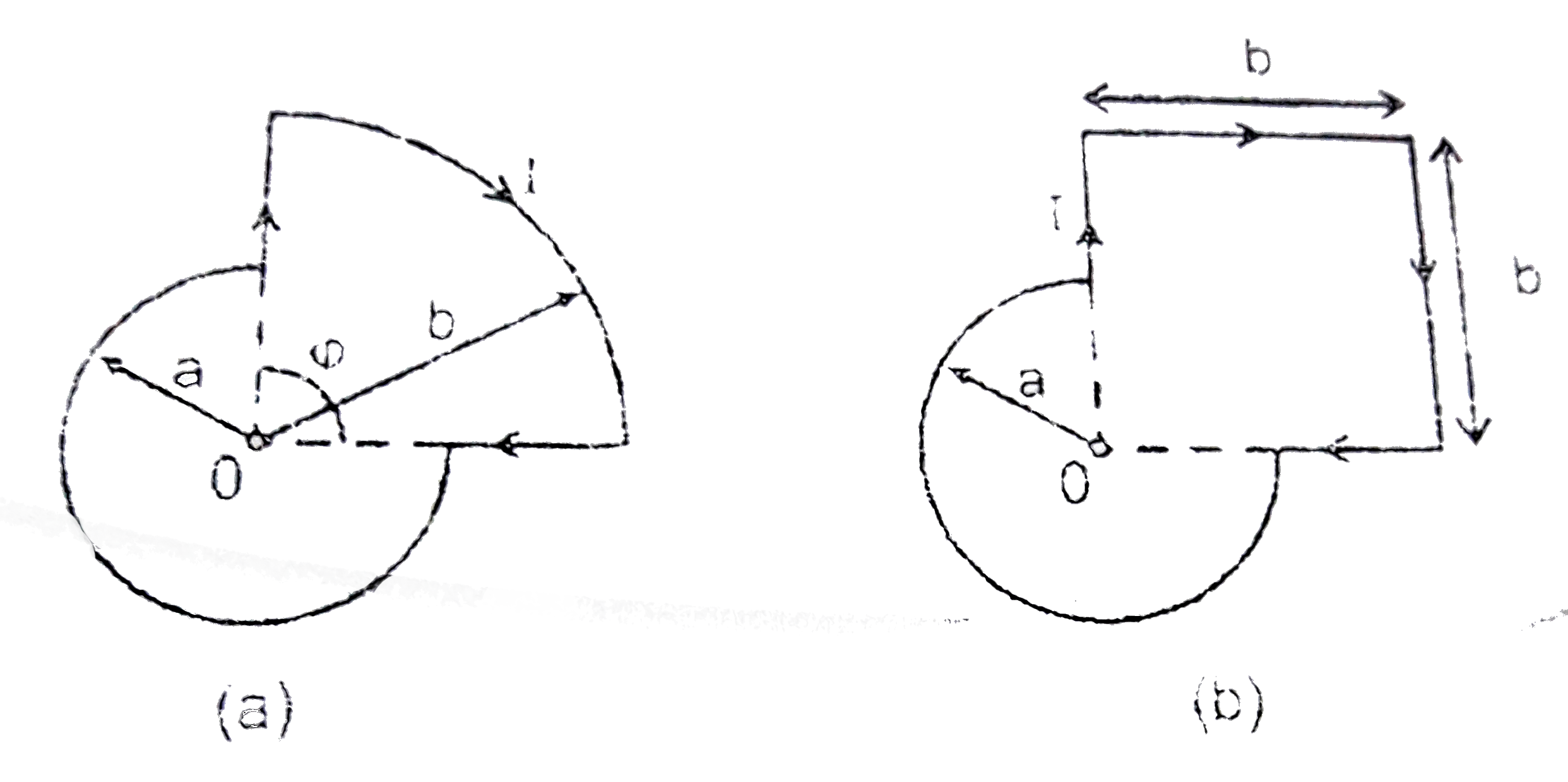
View SolutionA plane spiral with a great number N of turns wound tightly to one another is located in a uniform magnetic field perpendicular to the spiral's plane.The outside radius of the spiral's turns is equal to a and inner radius is zero.The magnetic induction varies with time as B=B0sinωt, where B0 and ω are constants.The amplitude of emf induced in the spiral is εim=1xπa2NωB0.Find out value of x.
View Solution(a) Calculate the self-inductance of a solenoid that is tightly wound with wire of diameter 0.10cm, has a cross-sectional area 0.90cm2 and is 40cm long
(b) If the current through the solenoid decreases uniformly from 10 A to 0A in 0.10s, what is the emf induced between the ends of the solenoid?
View SolutionCalculate the drift speed of the electrons when 1A of current exists in a copper wire of cross section 2 mm2.The number of free electrons in 1cm3of copper is 8.5×1022.
View SolutionA thin wire is wound very tightly in one layer on the surface of a sphere of paramagnetic material (μr≈1). The planes of all the turns can be assumed to be perpendicular to the same diameter of the sphere. The turns over the entire surface of the sphere. The radius of the sphere is R, the total number of turns is N, and the current in the winding is I. Find the magnetic induction at the centre of the sphere. (Given μ0NI=20R)
View Solution
