Question

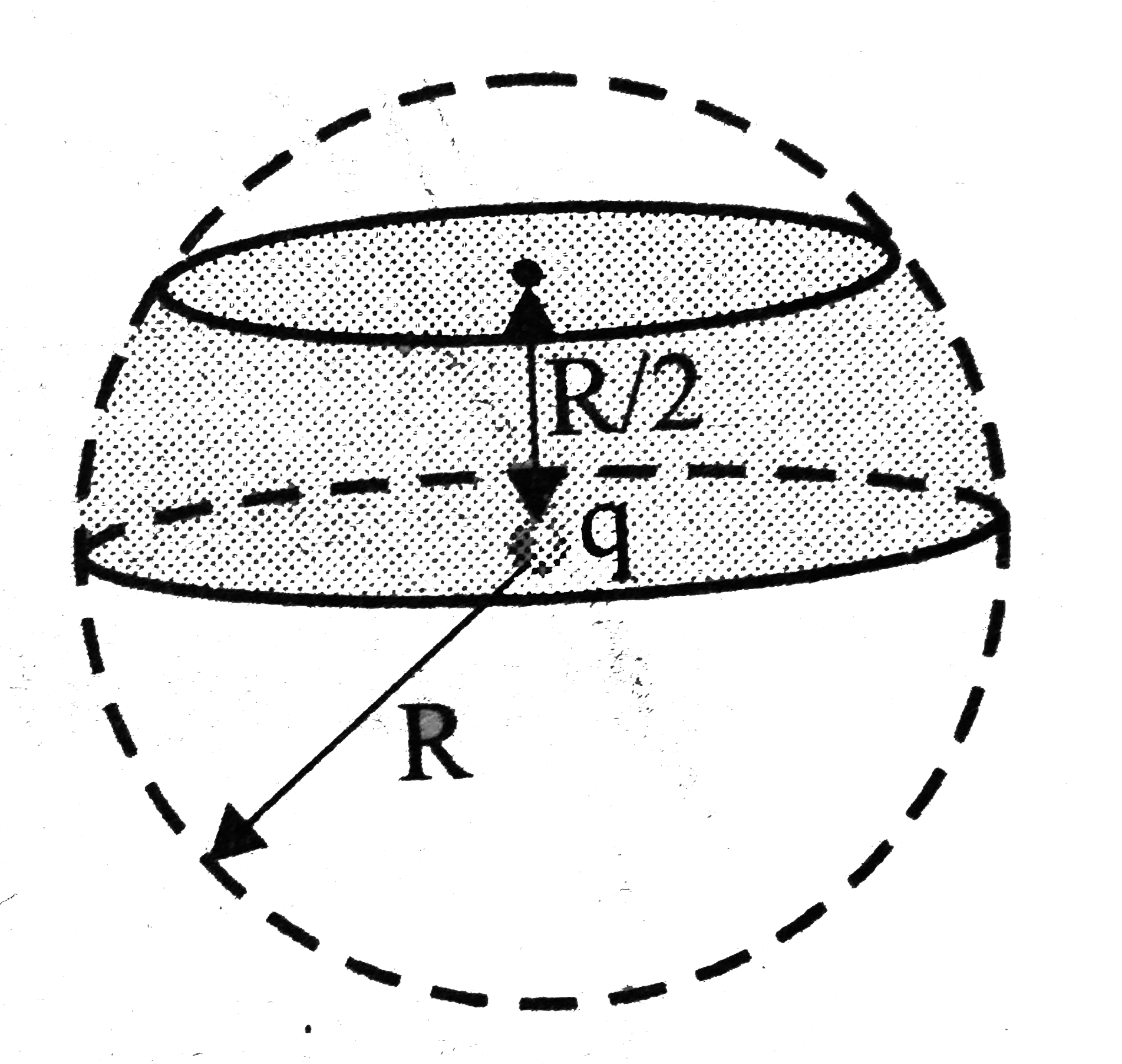
A thin wire is wound very tightly in one layer on the surface of a sphere of paramagnetic material $({\mu }_r\approx 1)$. The planes of all the turns can be assumed to be perpendicular to the same diameter of the sphere. The turns over the entire surface of the sphere. The radius of the sphere is $R$, the total number of turns is $N$, and the current in the winding is $I$. Find the magnetic induction at the centre of the sphere. (Given ${\mu }_{0}NI=20R$)

Explanation

To solve the problem of finding the magnetic induction at the center of a sphere wound with a thin wire, we can follow these steps:

Step 1: Understand the Geometry
We have a sphere of radius \( R \) with a thin wire wound tightly around it in one layer. The wire creates \( N \) turns, and the current flowing through the wire is \( I \). The planes of the wire turns are perpendicular to a diameter of the sphere.

Hint: Visualize the sphere and the wire wrapped around it. Recognize that the wire creates a magnetic field due to the current flowing through it.

Step 2: Determine the Magnetic Field Contribution from a Ring
Consider a small ring of the wire at an angle \( \theta \) from the center of the sphere. The radius of this ring can be expressed as \( r \sin \theta \), where \( r \) is the radius of the sphere. The magnetic field \( dB \) at the center of the sphere due to this ring can be calculated using the formula:

\( dB = \frac{\mu_0 I \, dN}{2 \pi (r \sin \theta)^2} \)

where \( dN \) is the number of turns in the ring.

Hint: Remember that the magnetic field produced by a current-carrying loop at its center is proportional to the current and the number of turns, and inversely proportional to the square of the radius.

Step 3: Calculate the Number of Turns in the Ring
The total number of turns \( N \) is distributed uniformly over the sphere. The angle \( \theta \) varies from \( 0 \) to \( \pi \). The elemental number of turns \( dN \) for the small angle \( d\theta \) can be expressed as:

\( dN = \frac{N}{\pi} d\theta \)

Hint: The total angle around the sphere is \( \pi \), and thus the number of turns per unit angle can be derived from the total number of turns.

Step 4: Substitute and Integrate
Substituting \( dN \) into the expression for \( dB \):

\( dB = \frac{\mu_0 I \, \frac{N}{\pi} d\theta}{2 \pi (R \sin \theta)^2} \)

This simplifies to:

\( dB = \frac{\mu_0 I N}{2 \pi^2 R^2 \sin^2 \theta} d\theta \)

Now, we need to integrate \( dB \) from \( 0 \) to \( \pi \):

\( B = \int_0^\pi dB = \int_0^\pi \frac{\mu_0 I N}{2 \pi^2 R^2 \sin^2 \theta} d\theta \)

Hint: Use the integral of \( \sin^2 \theta \) to simplify the calculation.

Step 5: Evaluate the Integral
Using the identity \( \sin^2 \theta = \frac{1 - \cos(2\theta)}{2} \), the integral can be evaluated:

\( \int_0^\pi \sin^2 \theta \, d\theta = \frac{\pi}{2} \)

Thus, substituting back into the equation for \( B \):

\( B = \frac{\mu_0 I N}{2 \pi^2 R^2} \cdot \frac{\pi}{2} \)

This simplifies to:

\( B = \frac{\mu_0 I N}{4 \pi R^2} \)

Step 6: Use the Given Condition
We are given that \( \mu_0 N I = 20R \). Substituting this into our expression for \( B \):

\( B = \frac{20R}{4 \pi R^2} = \frac{5}{\pi R} \)

Final Answer
Thus, the magnetic induction at the center of the sphere is:

\( B = \frac{5}{\pi R} \)