Figure shows a coil of single turn would on a sphere of radius R and mass m. The plane of the coil is parallel to the plane and lies in the equatorial plane of the sphere. What is the value of B if the sphere is in equilibrium when current in the coil is I?
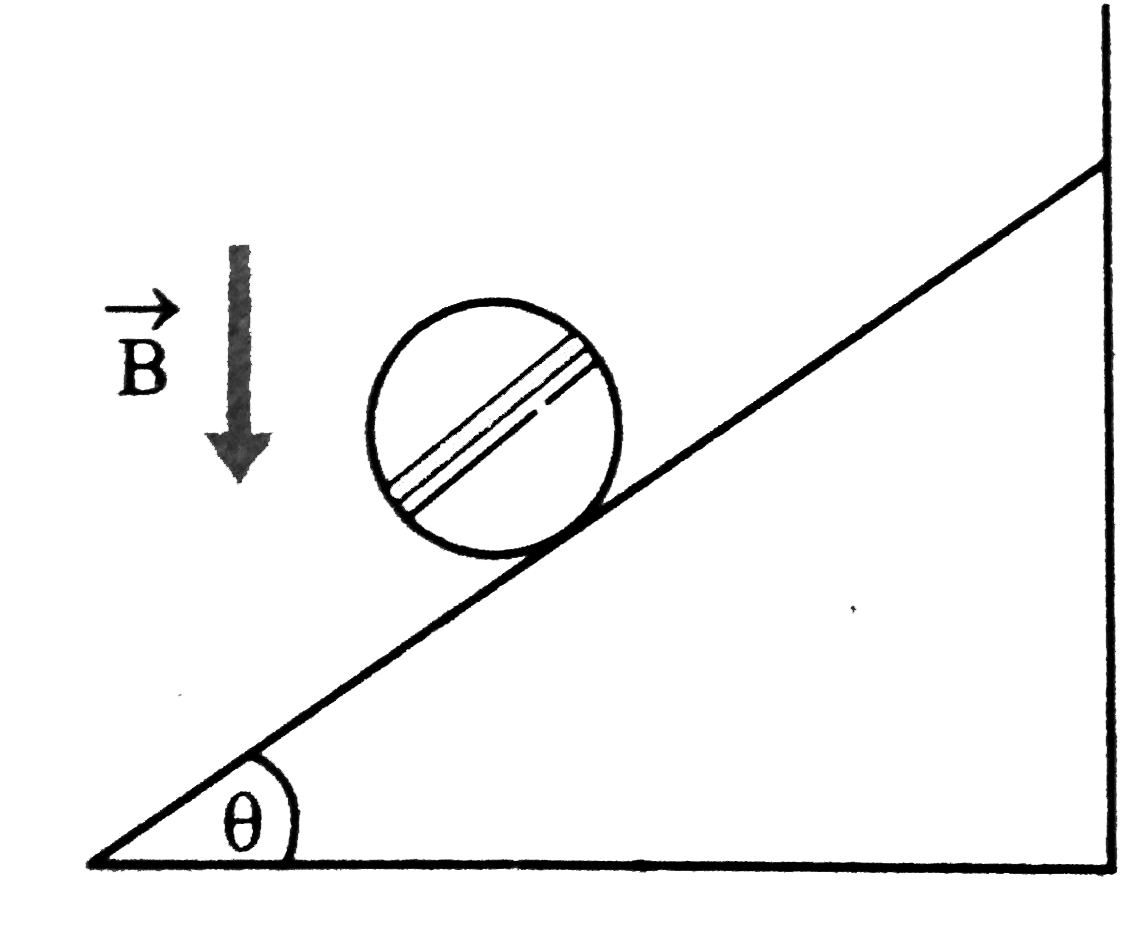
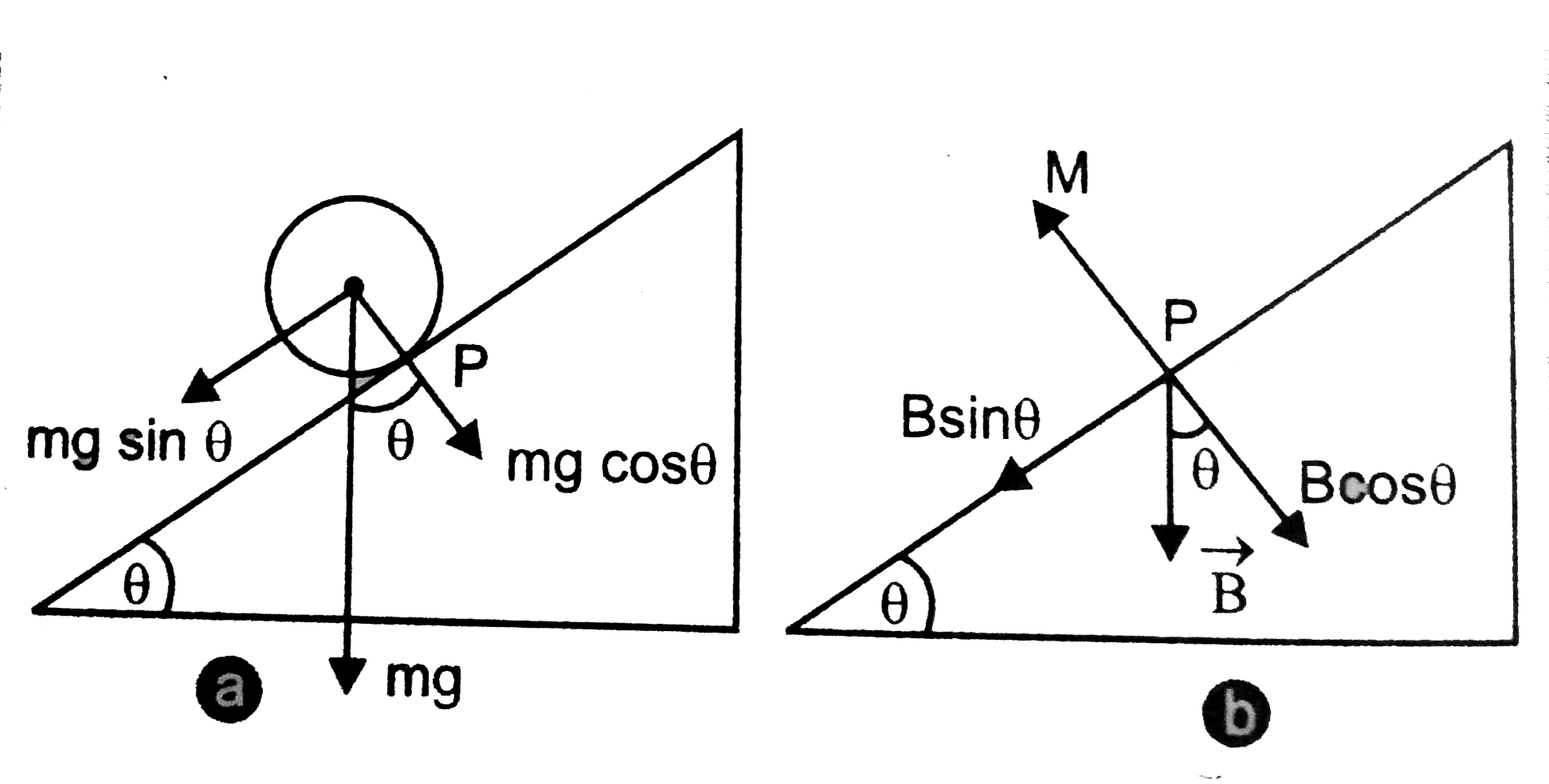
Magnetic dipole of moment of the coil carrying current, M=IπR2
Its direction is perpendicular to the plane acting upwards. Resolving →B into two rectangular components, we have Bcosθ acting ⊥r to the plane downwards and Bsinθ acting along the plane downwards, Fig.
For rotational equilibrium of sphere about point P is
(mgsinθ)R=M(Bsinθ) or mgRsinθ=IπR2Bsinθ or B=mgπIR
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Conceptual Problems (d)
Explore 2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Very Short Answer Questions (a)
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
If a sphere of radius 10 cm is intersected by a plane at a distance 8 cm from its centre, what is the radius of the curve of intersection of the plane and the sphere?
View SolutionA coil is placed in a constant magnetic field. The magnetic field is parallel to the plane of the coil as shown in Fig. 3.28. Find the emf induced in the coil if B increasing.

View Solution
Knowledge Check
In Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]
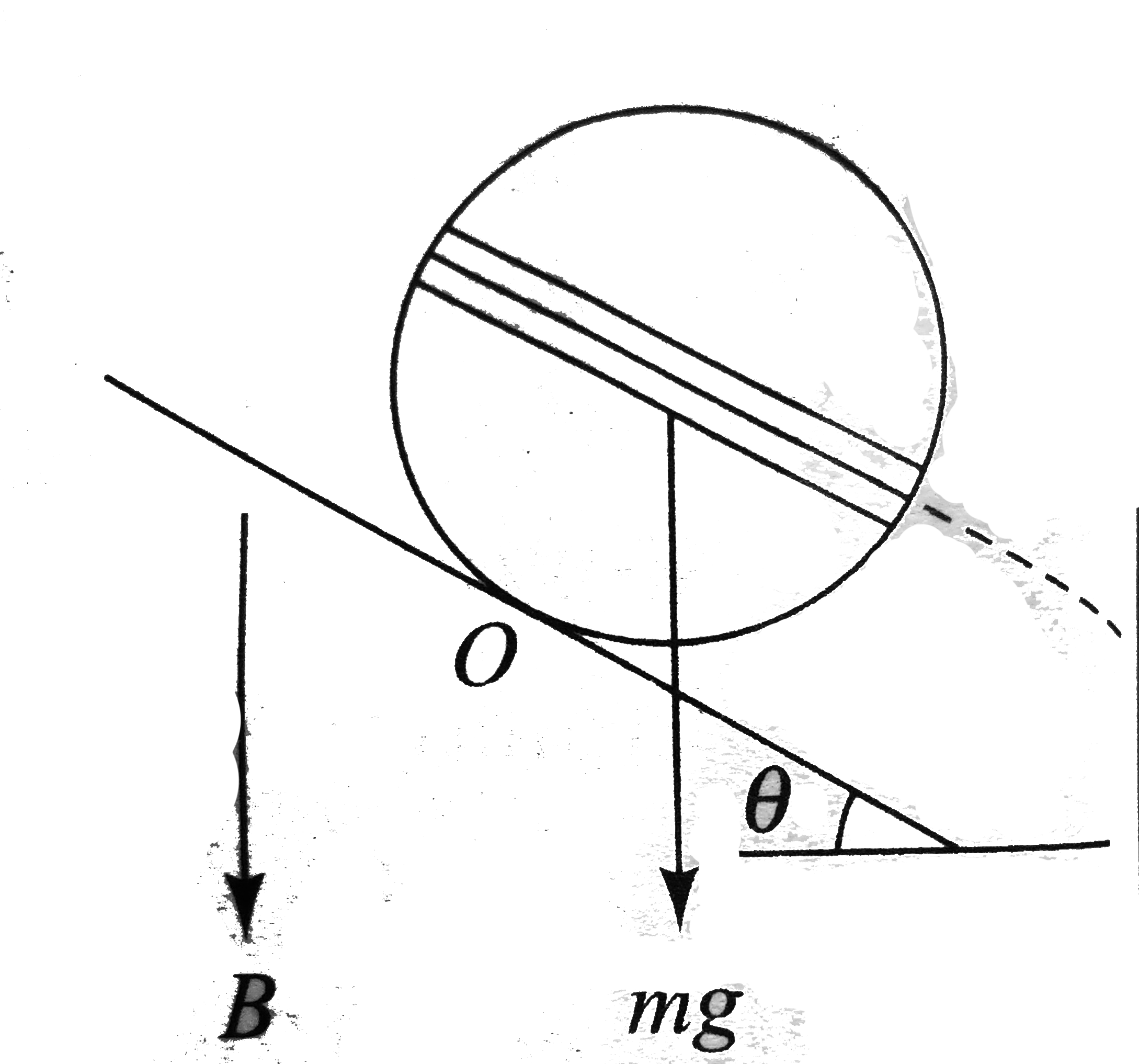 AmgπirBmgsinθπiCmgsinθπiDNone of these
AmgπirBmgsinθπiCmgsinθπiDNone of theseCurrent I is flowing through a circular coil of radius r. It is placed in a magnetic field B0 in such a way that the plane of the circular coil is perpendicular to B0. The force acting in it will be -
AParallel to BBIs perpendicular to BCAt45∘ with BDAt 60∘ with BThree mutually, tangent spheres of radius 1 rest on a horizontal plane. A sphere of radius 2 rests on them. What is the distance from the plane to the top of the larger sphere?
A3+√302B3+√693C3+√1234D529
A coil of radius r is placed at the centre of R>>r and coils are in same plane.The coefficient of mutual inductance between the coil is
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA current i flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
View SolutionA current i flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
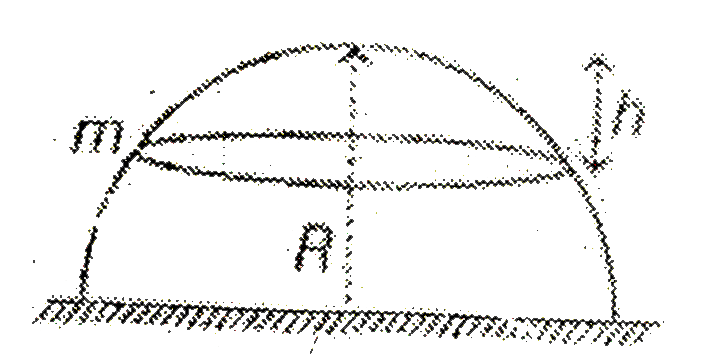
View SolutionA unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
View Solution

