In the above question, the correct value of focal length f of lens as calculated from the graph is :
f=1OA
f=1OA+OB
f=1OA−OB
f=1OB
The correct Answer is:D
In a convex lens, when object is at infinity, image is at focus, i.e.
when u=∞,1u=0,
1v=OB=1f∴F=1/OB.
Topper's Solved these Questions
Similar Questions
An object is placed in front of a converging lens at a distance equal to twice the focal length f1 of the lens. On the other side of the lens is a concave mirror of focal length f2 separated from the lens is a concave mirror of focal length f2 separated from the lens by a distance 2(f1+f2). Light from the object passes rightward through the lens, reflects from the mirror, passes leftward throught the lens, and forms a final image of the object.

View SolutionCalculate the focal length of the lens shown in the figure.
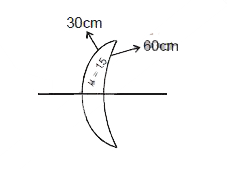
View Solution
Knowledge Check
An object is placed in front of a converging lens at a distance equal to twice the focal length f1 of the lens. On the other side of the lens is a concave mirror of focal length f2 separated from the lens is a concave mirror of focal length f2 separated from the lens by a distance 2(f1+f2). Light from the object passes rightward through the lens, reflects from the mirror, passes leftward throught the lens, and forms a final image of the object.
 AThe distance between the lens and the final image is equal to 2f1.BThe distance between the lens and the final image is equal to 2(f1+f2)CThe final image is real, inverted and of same size as that fo the object.DThe final image is real, erect and of same size as that of the object.
AThe distance between the lens and the final image is equal to 2f1.BThe distance between the lens and the final image is equal to 2(f1+f2)CThe final image is real, inverted and of same size as that fo the object.DThe final image is real, erect and of same size as that of the object.The power (P) of a lens of focal length (f) is given by
AP = fBP=1fCP=−1fDP=−fThe figure shows an equiconvex lens of focal length f. If the lens is cut along PQ ,the focal length of each half will be
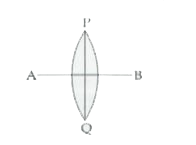 Af/2Bfrequent absorption of star light by earth's atmosphereC2fD4f
Af/2Bfrequent absorption of star light by earth's atmosphereC2fD4f
The focal length of the lens used in question 118 is
View SolutionThe figure shows and equiconvex lens of focal length f. It the lens is cut along PQ, the focal length of each half will be

View SolutionThe focal length of the lens used in question 118 is
View SolutionThe figure shows and equiconvex lens of focal length f. It the lens is cut along PQ, the focal length of each half will be

View SolutionA convex lens of focal length 'f' is placed in contact with a concave lens of the same focal length. The equivalent focal length of the combination is
View Solution

