The focal length of the lens used in question 118 is
D2+d22D
D2−d24D
D2−d22D
D2+d2d
The correct Answer is:b.
To find the focal length of the lens used in the problem, we can follow these steps:
Step 1: Understand the Problem
We have a convex lens that is placed in two different positions while forming the image on the same screen. The distance between the two positions of the lens is denoted as d, and the total distance between the object and the screen is denoted as D.
Step 2: Set Up the Lens Displacement Equations
From the lens displacement formula, we can establish two equations based on the positions of the lens:
1. V+u=D (for the first position)
2. V−u=d (for the second position)
Where:
- V is the image distance,
- u is the object distance.
Step 3: Solve for V and u
We can add the two equations to eliminate u:
(V+u)+(V−u)=D+d
This simplifies to:
2V=D+d⟹V=D+d2
Next, we subtract the second equation from the first to eliminate V:
(V+u)−(V−u)=D−d
This simplifies to:
2u=D−d⟹u=D−d2
Step 4: Use the Lens Formula
The lens formula relates the focal length f to the object distance u and the image distance V:
1f=1V−1u
Substituting the values of V and u:
1f=2D+d−2D−d
Step 5: Find a Common Denominator
To combine the fractions, we need a common denominator:
1f=2(D−d)−2(D+d)(D+d)(D−d)
This simplifies to:
1f=2D−2d−2D−2d(D+d)(D−d)=−4d(D+d)(D−d)
Step 6: Solve for f
Taking the reciprocal gives us:
f=(D+d)(D−d)−4d=D2−d24d
Conclusion
The focal length f of the lens is:
f=D2−d24d
We have a convex lens that is placed in two different positions while forming the image on the same screen. The distance between the two positions of the lens is denoted as d, and the total distance between the object and the screen is denoted as D.
From the lens displacement formula, we can establish two equations based on the positions of the lens:
1. V+u=D (for the first position)
2. V−u=d (for the second position)
- V is the image distance,
- u is the object distance.
We can add the two equations to eliminate u:
(V+u)+(V−u)=D+d
This simplifies to:
2V=D+d⟹V=D+d2
(V+u)−(V−u)=D−d
This simplifies to:
2u=D−d⟹u=D−d2
The lens formula relates the focal length f to the object distance u and the image distance V:
1f=1V−1u
1f=2D+d−2D−d
To combine the fractions, we need a common denominator:
1f=2(D−d)−2(D+d)(D+d)(D−d)
This simplifies to:
1f=2D−2d−2D−2d(D+d)(D−d)=−4d(D+d)(D−d)
Taking the reciprocal gives us:
f=(D+d)(D−d)−4d=D2−d24d
The focal length f of the lens is:
f=D2−d24d
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Find the focal length of the lens used.
View SolutionFind the focal length of the lens shown in Fig.
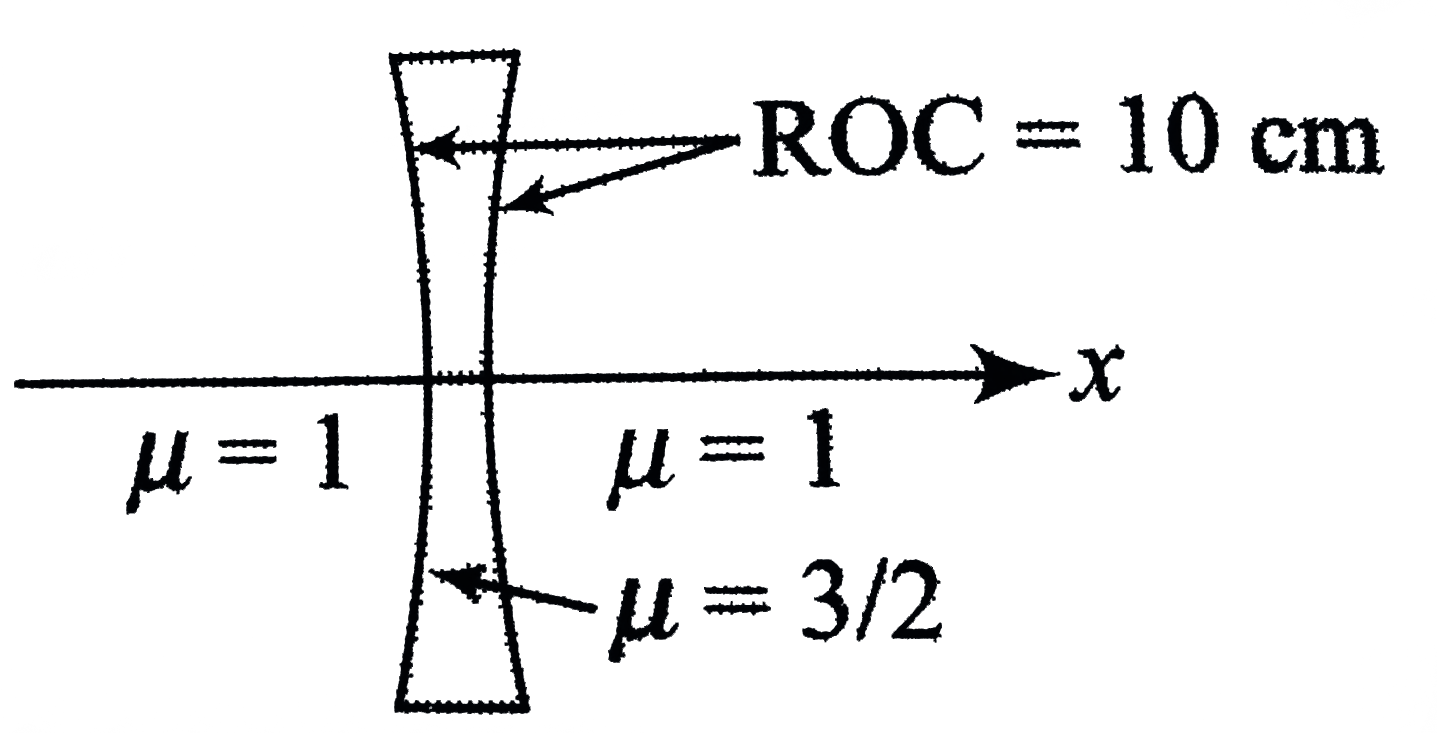
View SolutionA doctor has prescribed lens of power +1.5D. Find the focal length of the lens. Is the prescribed lens diverging or converging ?
View SolutionThe distance between an object and a divergent lens is m times the focal length of the lens. The linear magnification produced by the lens is
View SolutionThe power of lens is P=1f' where f is focal length of the lens. The dimensions of power of lens is
View SolutionThe power of lens is P=1f where f is focal length of the lens. The dimensions of power of lens is
View SolutionFind the focal length of the lens shown in the Fig..
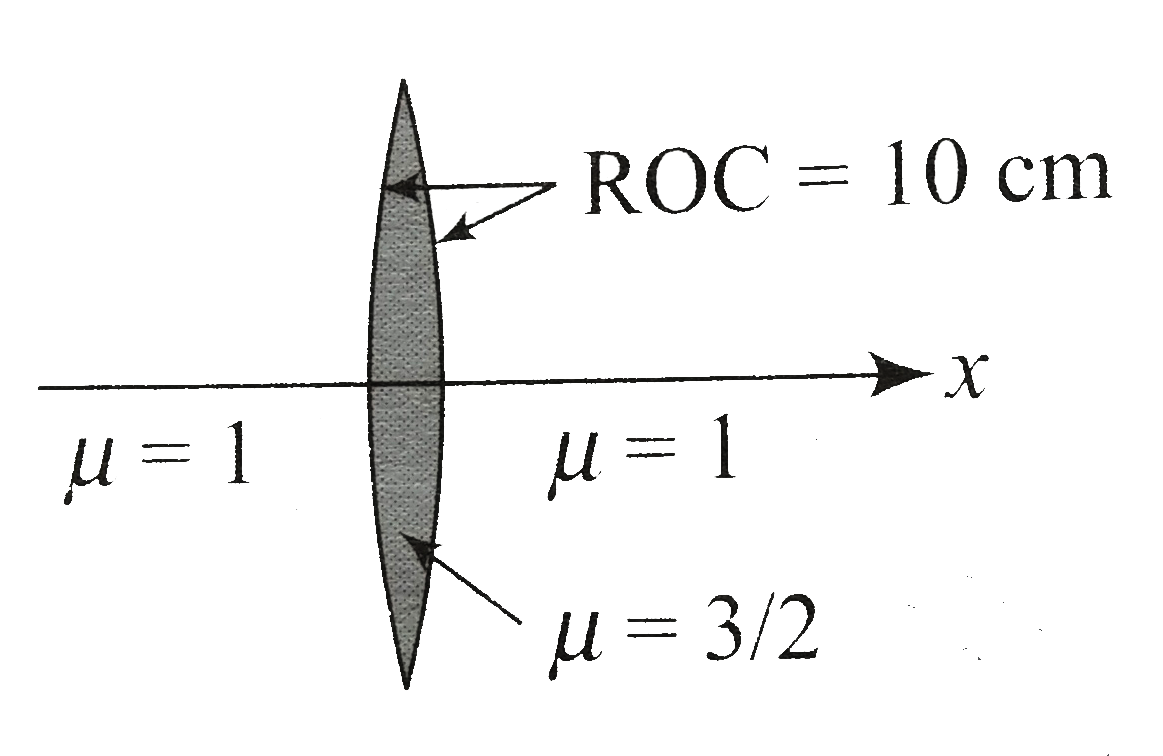
View SolutionThe dispersive power of the material of a lens is 0.04 and the focal length of the lens is 10cm. Find the difference in the focal length (in mm) of the lens for violet and red colour.
View SolutionThe change in focal length of an eye lens is caused by the action of the
View SolutionIf the focal length of objective lens is increased then magnifying power of
View Solution
