A neutral atom of atomic mass number 100 which is stationary at the origin in gravity free space emits an α-particle (A) in z-direction. The product ion is P. A uniform magnetic field exists in the x-direction. Disregard the electromagnetic interaction between A and P. If the angle of rotation of A after which A and P will meet for the first time is nπ25 radians, what is the value of n?
The correct Answer is:48
To solve the problem step by step, we will analyze the motion of the alpha particle (A) and the product ion (P) after the emission of the alpha particle from the neutral atom.
Step 1: Understand the system
- We have a neutral atom with an atomic mass number of 100, which emits an alpha particle (A) in the z-direction.
- The remaining product ion (P) will have a mass of 100−4=96 (since the mass of an alpha particle is 4).
- A uniform magnetic field exists in the x-direction.
Step 2: Determine the charges
- The alpha particle (A) has a charge of +2e.
- By conservation of charge, the product ion (P) must have a charge of −2e (to keep the total charge neutral).
Step 3: Calculate the angular velocities
- The angular velocity (ω) of a charged particle moving in a magnetic field is given by:
ω=qBm
- For the alpha particle (A):
ωA=(2e)B4m=eB2m
- For the product ion (P):
ωP=(−2e)B96m=−eB48m
Step 4: Determine the time until they meet
- The total angle rotated by both particles when they meet for the first time is 2π radians.
- The angles rotated by A and P can be expressed as:
θA+θP=2π
- The angles can be expressed in terms of time t:
θA=ωAtandθP=ωPt
- Substituting the angular velocities:
eB2mt−eB48mt=2π
- Factor out t:
t(eB2m−eB48m)=2π
- Combine the fractions:
t(24eB−eB48m)=2π
t(23eB48m)=2π
- Solving for t:
t=2π⋅48m23eB
Step 5: Calculate the angle for A
- Now, substituting t back to find the angle θA:
θA=ωAt=eB2m⋅2π⋅48m23eB
- Simplifying:
θA=48π23
Step 6: Relate to the given angle
- The problem states that the angle of rotation of A after which A and P will meet for the first time is nπ25.
- Setting the two expressions for θA equal:
48π23=nπ25
- Canceling π from both sides:
4823=n25
- Cross-multiplying to solve for n:
n=48⋅2523=120023≈52.17
- Since n must be an integer, we round down to the nearest whole number, which is 52.
Final Answer
Thus, the value of n is 52.
- We have a neutral atom with an atomic mass number of 100, which emits an alpha particle (A) in the z-direction.
- The remaining product ion (P) will have a mass of 100−4=96 (since the mass of an alpha particle is 4).
- A uniform magnetic field exists in the x-direction.
- The alpha particle (A) has a charge of +2e.
- By conservation of charge, the product ion (P) must have a charge of −2e (to keep the total charge neutral).
- The angular velocity (ω) of a charged particle moving in a magnetic field is given by:
ω=qBm
- For the alpha particle (A):
ωA=(2e)B4m=eB2m
- For the product ion (P):
ωP=(−2e)B96m=−eB48m
- The total angle rotated by both particles when they meet for the first time is 2π radians.
- The angles rotated by A and P can be expressed as:
θA+θP=2π
- The angles can be expressed in terms of time t:
θA=ωAtandθP=ωPt
- Substituting the angular velocities:
eB2mt−eB48mt=2π
- Factor out t:
t(eB2m−eB48m)=2π
- Combine the fractions:
t(24eB−eB48m)=2π
t(23eB48m)=2π
- Solving for t:
t=2π⋅48m23eB
- Now, substituting t back to find the angle θA:
θA=ωAt=eB2m⋅2π⋅48m23eB
- Simplifying:
θA=48π23
- The problem states that the angle of rotation of A after which A and P will meet for the first time is nπ25.
- Setting the two expressions for θA equal:
48π23=nπ25
- Canceling π from both sides:
4823=n25
- Cross-multiplying to solve for n:
n=48⋅2523=120023≈52.17
- Since n must be an integer, we round down to the nearest whole number, which is 52.
Thus, the value of n is 52.
Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Exercise-3 PART-3
Explore 29 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
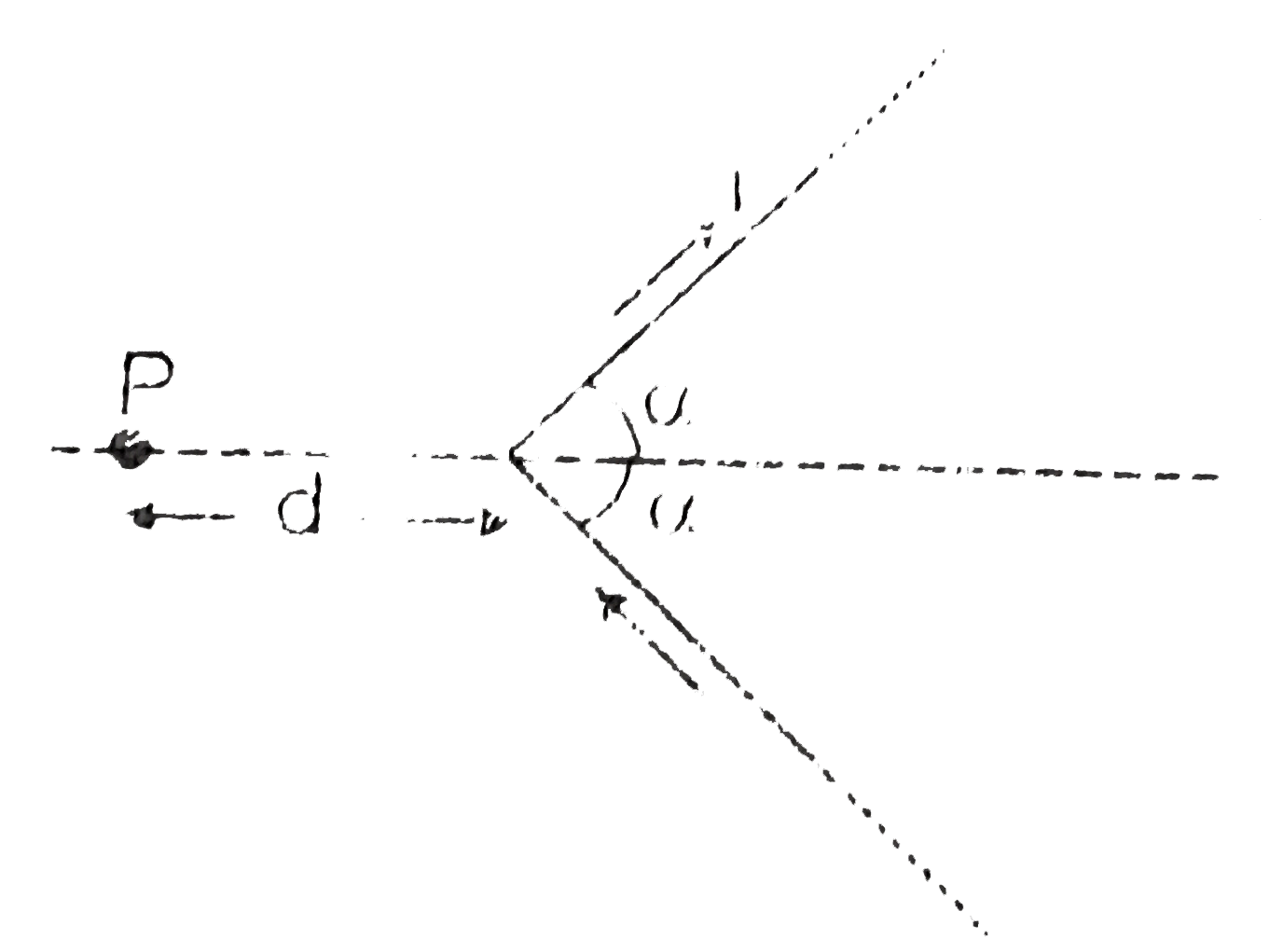
The direction of the field B at P is

View SolutionA charged particle begins to move from the origin in a region which has a uniform magnetic field in the x-direction and a uniform electric field in the y-direction. Its speed is v when it reaches the point (x, y, z). Then, v will depend
View SolutionA uniform but increasing with time magnetic field exists in as cylindrical region. The direction of force on an electron at P as

View SolutionA beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
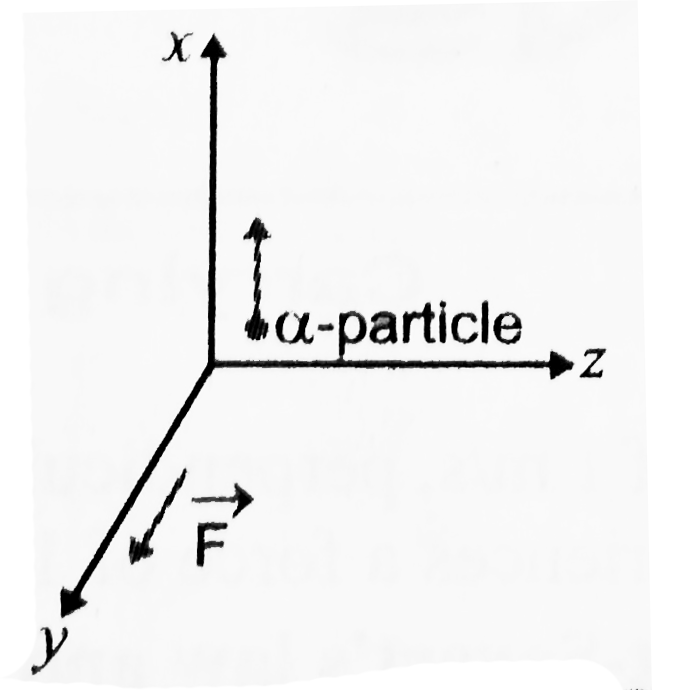
View SolutionIn a region of space, a uniform magnetic field B exists in the x-direction. An electron is fired from the origin with its initial velocity u making an angle α with the y direction in the y-z plane. In the subsequent motion of the electron,

View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionIn a region of space, a uniform magnetic field B exists in the y direction. A proton is fired from the origin, with its initial velocity v making a small angle α with the y direction in the yz plane. In the subsequent motion of the proton,

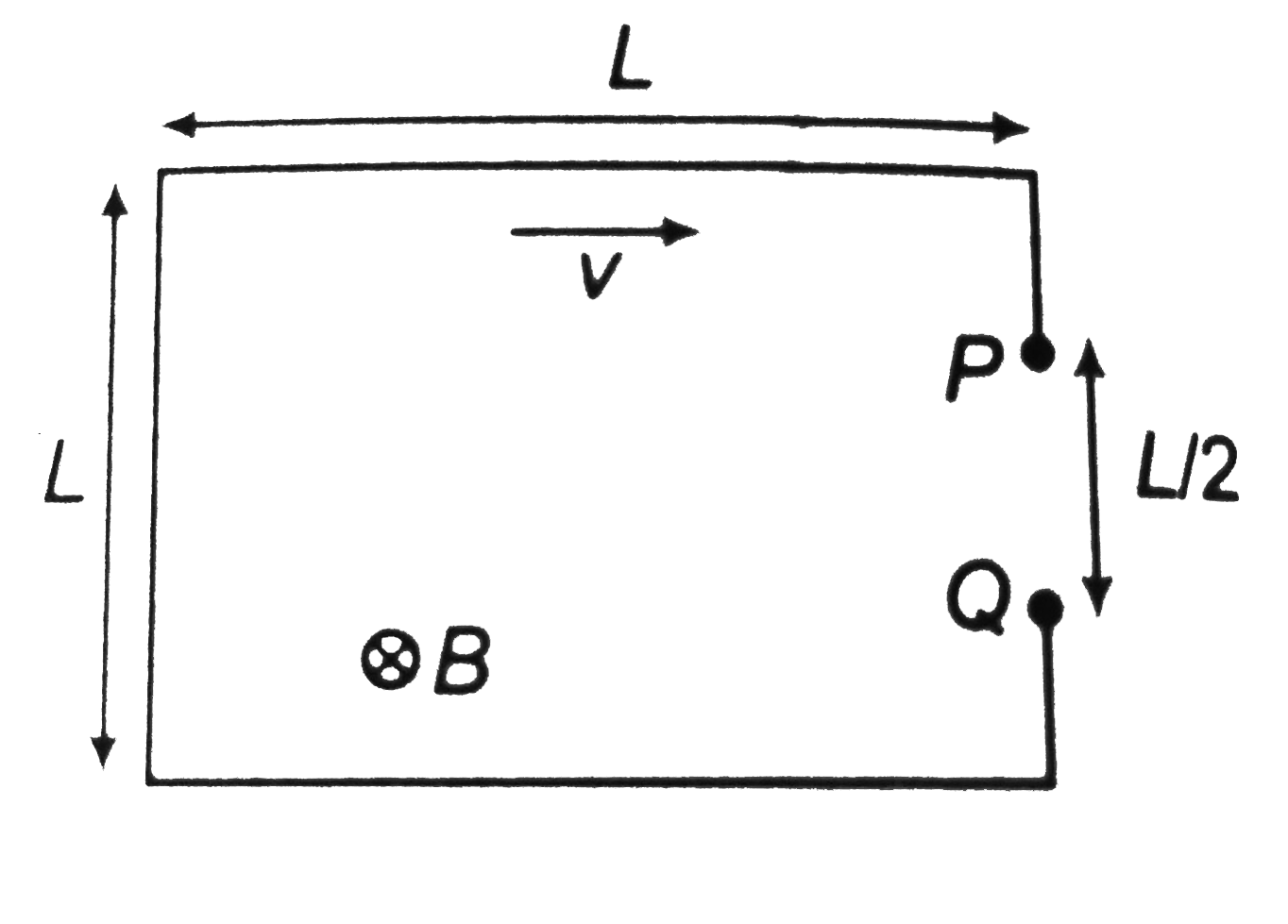
View SolutionThe loop shown moves with a velocity v in a uniform magnetic field of magnitude B, directed into the paper. The potential differene between point P and Q is e. Then
View SolutionA particle is released from rest from origin O. There is a uniform magnetic field in negative z-direction. Positive y-direction is vertically upwards. After falling through 5m the velocity vector makes an angle 30∘ with x-axis.

The path of the particle is
View SolutionPositive and negative ions are productid at the origin. If they are subjected simultaneously to an electric field along the +y−directionandmaGNeticfieldalong+z-direction, then
View Solution