A circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of the semicircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at the origin. Current I is flowing through each of the semicircles as shown in the figure.
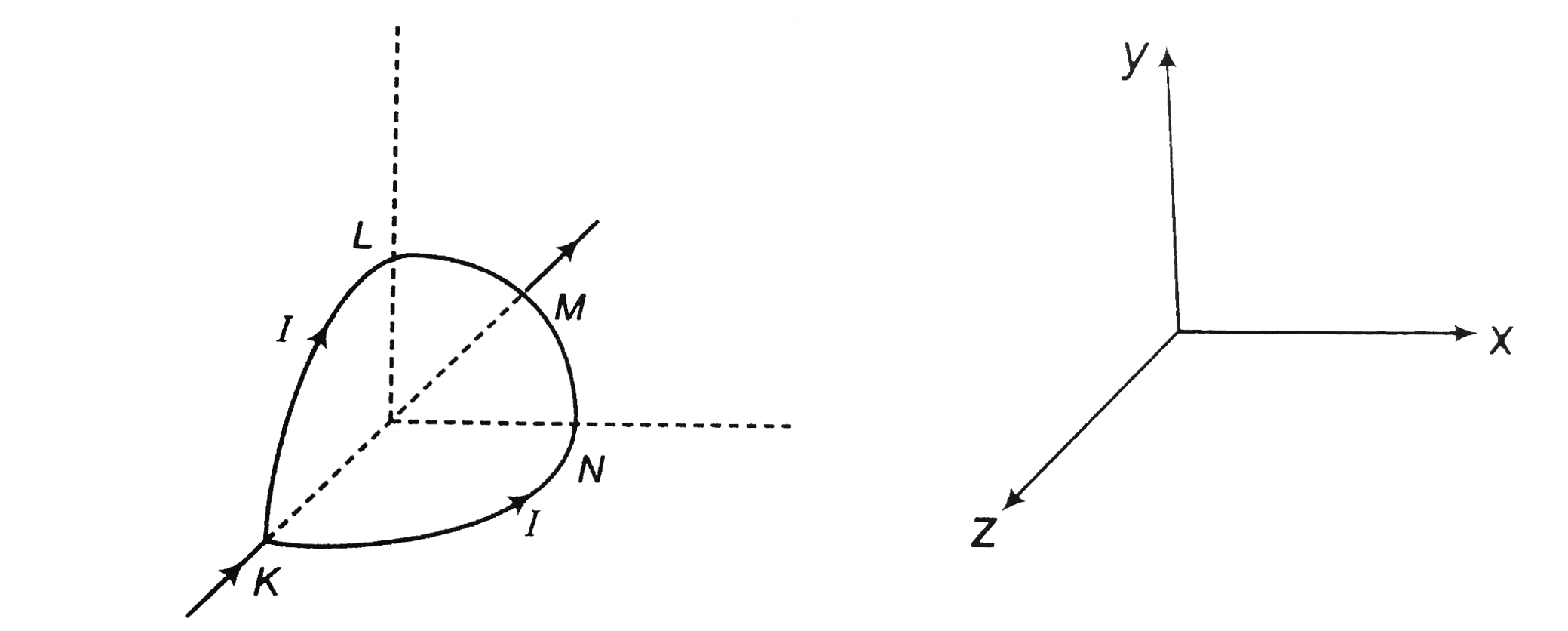
(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
The correct Answer is:(i)−μ0I4Rqv0ˆk (ii) 4lRBˆi
(a)Magnetic field (→B) at the origion =Magnetic field due to semicircle KLM+ Magnetic field due to other semicircle KNM
∴→B=μ0I4R(−ˆi)+μ0I4R(−ˆj)
→B=−μ0I4Rˆi+μ0I4Rˆj=μ0I4R(−ˆi+ˆj)
∴ Magnetic force acting on the particle-
→F=q(→v×→B)=q(−V0ˆi)×(−ˆi+ˆj)}μ0l4R
→F=−μ0qV0l4Rˆk
(b)→FKLM=→FKNM=→FKM
and →FKM=BI(2R)ˆi
=2BIRˆj
→F1=→F2=2BIRˆi
or Total force on the loop =→F=→F1+→F2
or →F=4BIRˆj
If a current carrying wire ADC (of any shape) is placed in a uniform magnetic field
→B.Then →FADC=→FACor∣∣→FADC∣∣=i(AC)B.
From this we can conclude that net force on a current carrying loop in uniform magnetic field is zero.In the question, segmets KLM and KNM also form a loop and they are also placed in a uniform magnetic field bu in this case net force on the loop will not be zero.It would had been zero it the current in any of the segments was in opposite direction.

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-3
29 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
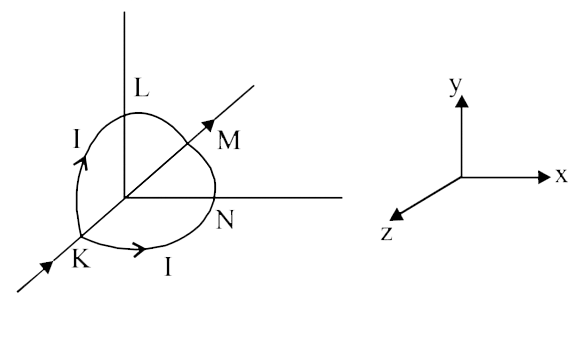
A circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30,A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure.

(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
View SolutionA circular loop of radius R is bent along a diameter and given a shapes as shown in the figure. One of the semicircles (KNM) lies in the x−z plane with their centres and the other one (KLM) in the y−z plane with their centres at the origin. current I is flowing through each of the semi circles as shown in figure.
(a) A particle of charge q is released at the origin with a velocity →v=−v0ˆi. Find the instantaneous force →F on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied , determine the force →F1and→F2 on the semicircles KLMandKNM due to the field and the net force →F on the loop.
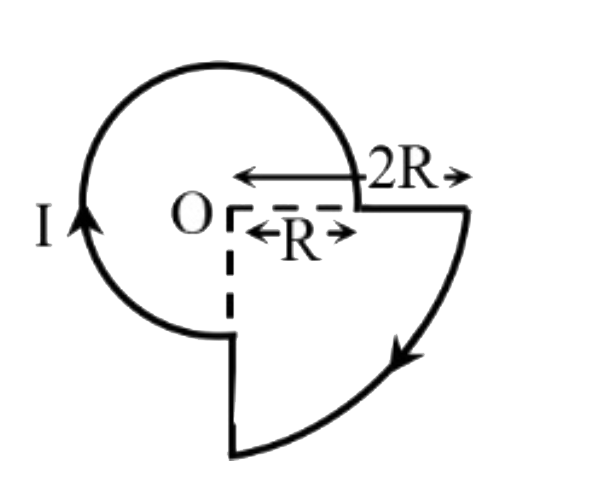
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
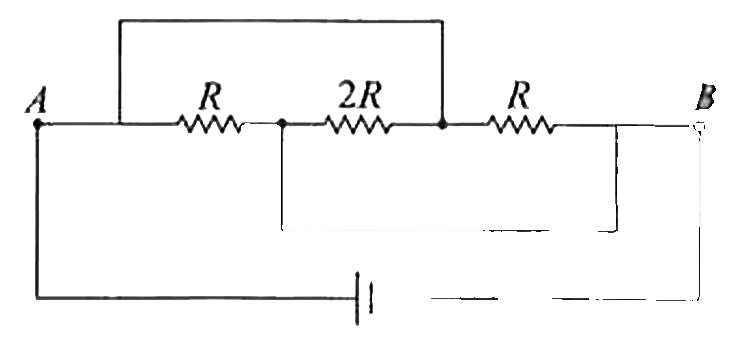
View SolutionIn the figure shown the current flowing through 2R is:
View SolutionA conductor is bent in the form of concentric semicircles as shown in the figure. The magnetic field at the point O is

View SolutionA circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
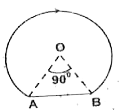
View SolutionA particle is moving in x-y plane as shown in the figure. Angular velocity of the particle with respect to the origin is
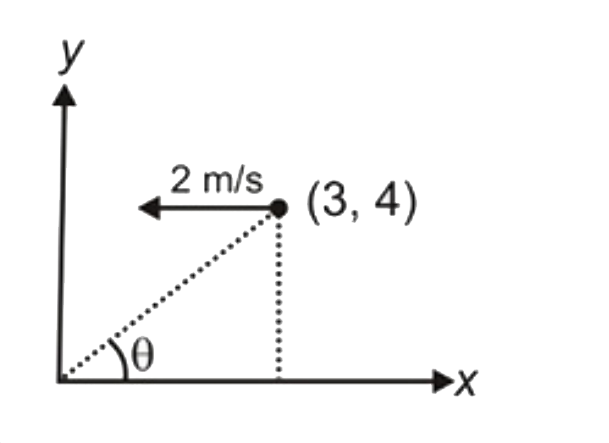
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
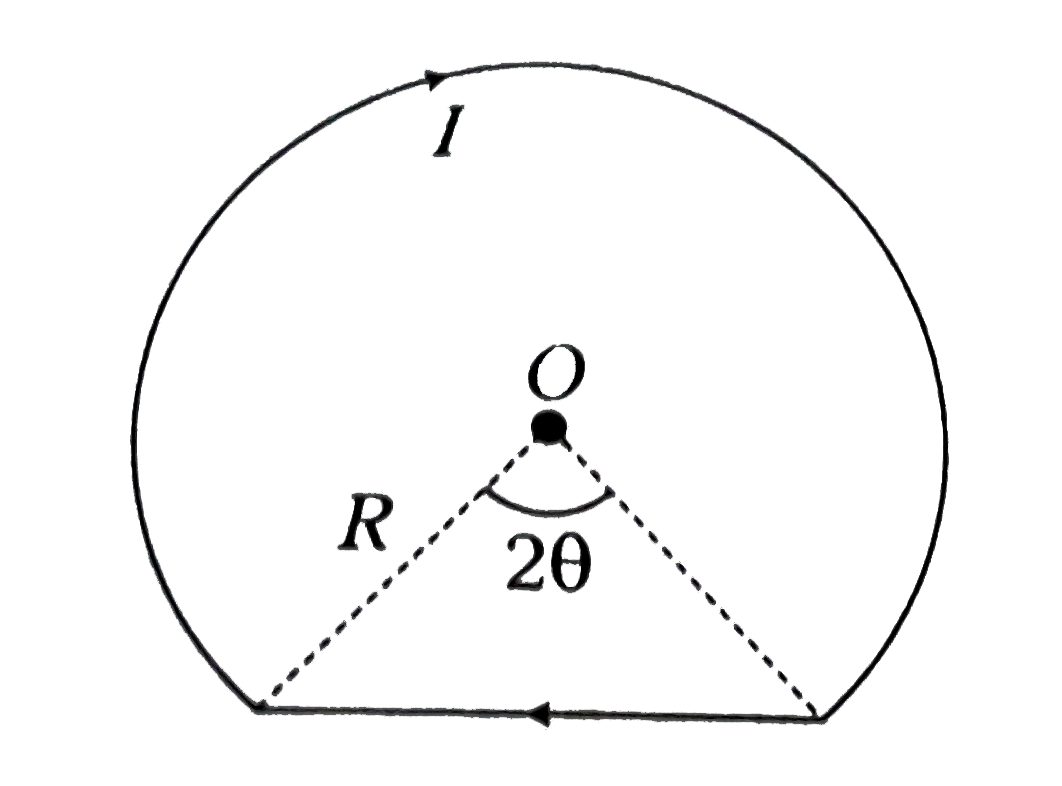
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View Solution
