Question

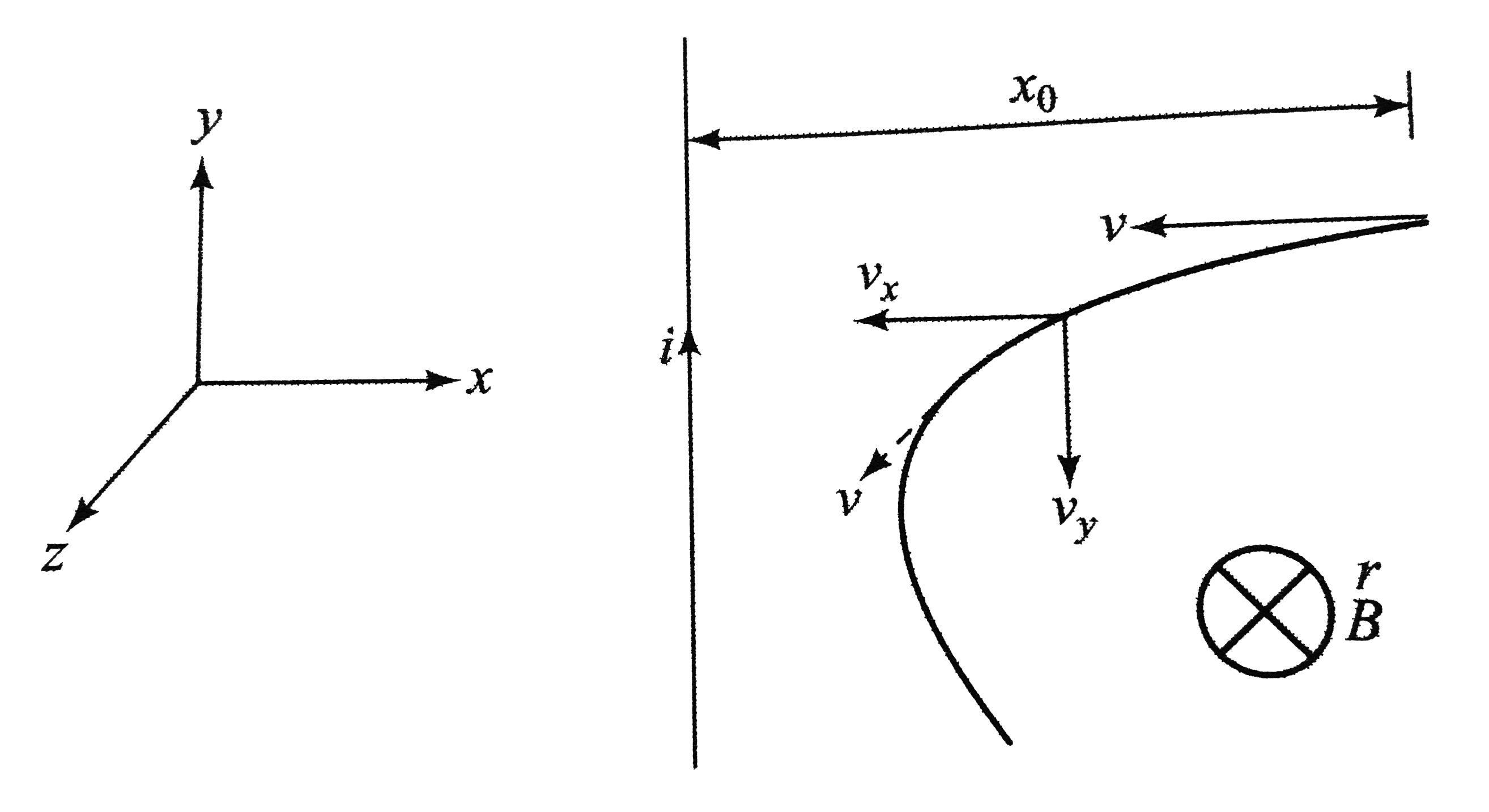
A positive point charge $q$ of mass $m$, kept at a distance $x_0$(in the same plane) from a fixed very long straight current is projected normally away from it with speed $v$.Find the maximum separation between the wire and the particle.

Explanation

To solve the problem of finding the maximum separation between a positive point charge $$q$$ of mass $$m$$, projected normally away from a fixed long straight current-carrying wire, we can follow these steps:

1. Understanding the Setup:
- We have a long straight wire carrying a current \( I \).
- A positive point charge \( q \) is located at a distance \( x_0 \) from the wire and is projected away from the wire with an initial speed \( v \).

2. Magnetic Field Due to the Wire:
- The magnetic field \( B \) at a distance \( r \) from a long straight wire carrying current \( I \) is given by:
\( B = \frac{\mu_0 I}{2 \pi r} \)
- At the initial distance \( x_0 \), the magnetic field becomes:
\( B = \frac{\mu_0 I}{2 \pi x_0} \)

3. Direction of Forces:
- The charge experiences a magnetic force due to its motion in the magnetic field. The direction of this force can be determined using the right-hand rule.
- If the current is in the positive \( y \)-direction and the velocity of the charge is in the positive \( x \)-direction, the magnetic field will be in the negative \( z \)-direction.

4. Magnetic Force on the Charge:
- The magnetic force \( F \) acting on the charge \( q \) is given by:
\( F = q \cdot (v \times B) \)
- Since \( v \) is in the \( x \)-direction and \( B \) is in the negative \( z \)-direction, the force will act in the \( y \)-direction.

5. Equations of Motion:
- The magnetic force will cause the charge to experience a centripetal acceleration. The magnetic force can be expressed as:
\( F = q \cdot v \cdot B = \frac{\mu_0 q I v}{2 \pi x_0} \)
- This force acts perpendicular to the velocity of the charge, causing it to move in a circular path.

6. Conservation of Energy:
- As the charge moves away from the wire, it will convert its kinetic energy into potential energy due to the magnetic field.
- The total mechanical energy (kinetic + potential) at the maximum separation can be expressed as:
\( \frac{1}{2} m v^2 = \frac{\mu_0 q I}{2 \pi} \ln\left(\frac{x}{x_0}\right) \)
- Here, \( x \) is the maximum distance from the wire.

7. Solving for Maximum Separation:
- Rearranging the energy equation gives:
\( \ln\left(\frac{x}{x_0}\right) = \frac{2 \pi m v^2}{\mu_0 q I} \)
- Exponentiating both sides results in:
\( \frac{x}{x_0} = e^{\frac{2 \pi m v^2}{\mu_0 q I}} \)
- Thus, the maximum separation \( x \) is:
\( x = x_0 e^{\frac{2 \pi m v^2}{\mu_0 q I}} \)

Final Answer
The maximum separation between the wire and the particle is:
\( x = x_0 e^{\frac{2 \pi m v^2}{\mu_0 q I}} \)