Consider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
To find the maximum velocity of projection for which a charged particle does not hit a metal sheet, we can follow these steps:
Step 1: Understand the Forces Acting on the Particle
The charged particle experiences a magnetic force due to the magnetic field created by the current in the metal sheet. The magnetic force F acting on the particle can be expressed as:
F=q(v×B)
where q is the charge of the particle, v is the velocity of the particle, and B is the magnetic field.
Step 2: Determine the Magnetic Field
From the previous example, we know that the magnetic field B at a distance d from the sheet is given by:
B=μ0I2πd
However, for our calculation, we can simplify this to B=μ0k2 where k is a constant related to the current.
Step 3: Set Up the Equation for the Force
The magnetic force acting on the particle can also be expressed in terms of the centripetal force required to keep the particle in circular motion:
F=mv2d
where m is the mass of the particle, v is its velocity, and d is the distance from the sheet.
Step 4: Equate the Forces
Since the magnetic force provides the necessary centripetal force, we can set the two expressions for force equal to each other:
qBv=mv2d
Step 5: Substitute the Expression for Magnetic Field
Substituting B into the equation gives:
q(μ0k2)v=mv2d
Step 6: Rearrange the Equation
Rearranging the equation to solve for v:
qμ0k2v=mv2d
qμ0k2=mvd
v=qμ0kd2m
Step 7: Conclusion
Thus, the maximum velocity of projection for which the particle does not hit the sheet is given by:
v=μ0kqd2m
The charged particle experiences a magnetic force due to the magnetic field created by the current in the metal sheet. The magnetic force F acting on the particle can be expressed as:
F=q(v×B)
where q is the charge of the particle, v is the velocity of the particle, and B is the magnetic field.
From the previous example, we know that the magnetic field B at a distance d from the sheet is given by:
B=μ0I2πd
However, for our calculation, we can simplify this to B=μ0k2 where k is a constant related to the current.
The magnetic force acting on the particle can also be expressed in terms of the centripetal force required to keep the particle in circular motion:
F=mv2d
where m is the mass of the particle, v is its velocity, and d is the distance from the sheet.
Since the magnetic force provides the necessary centripetal force, we can set the two expressions for force equal to each other:
qBv=mv2d
Substituting B into the equation gives:
q(μ0k2)v=mv2d
Rearranging the equation to solve for v:
qμ0k2v=mv2d
qμ0k2=mvd
v=qμ0kd2m
Thus, the maximum velocity of projection for which the particle does not hit the sheet is given by:
v=μ0kqd2m
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A uniform magnetic field ¯¯¯B=B0ˆj exists in a space. A particle of mass m and charge q is projected towards negative x-axis with speed v from the a point (d,0,0) The maximum value v for which the particle does not hit y−z plane is .
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
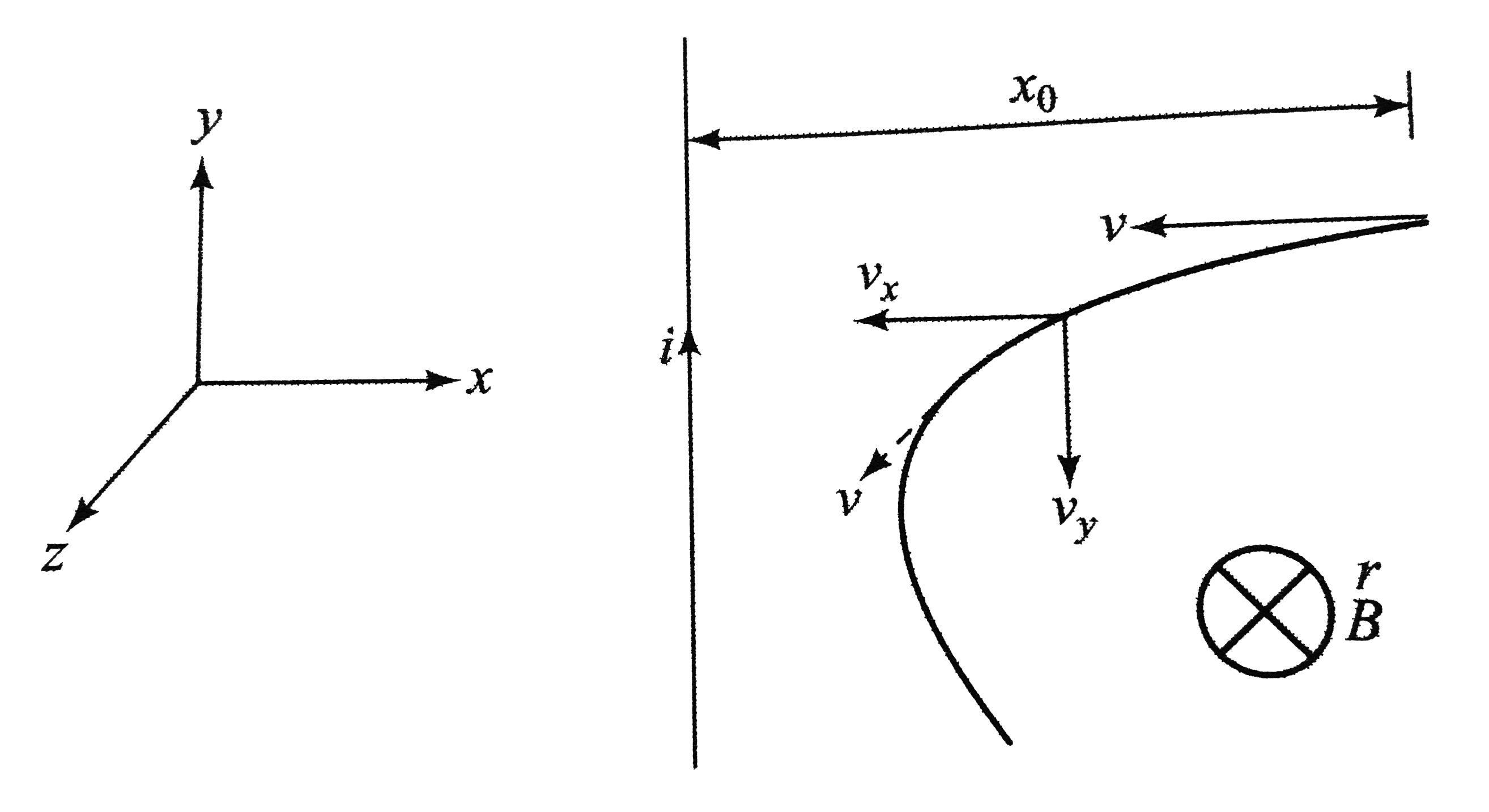

View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
View SolutionA tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
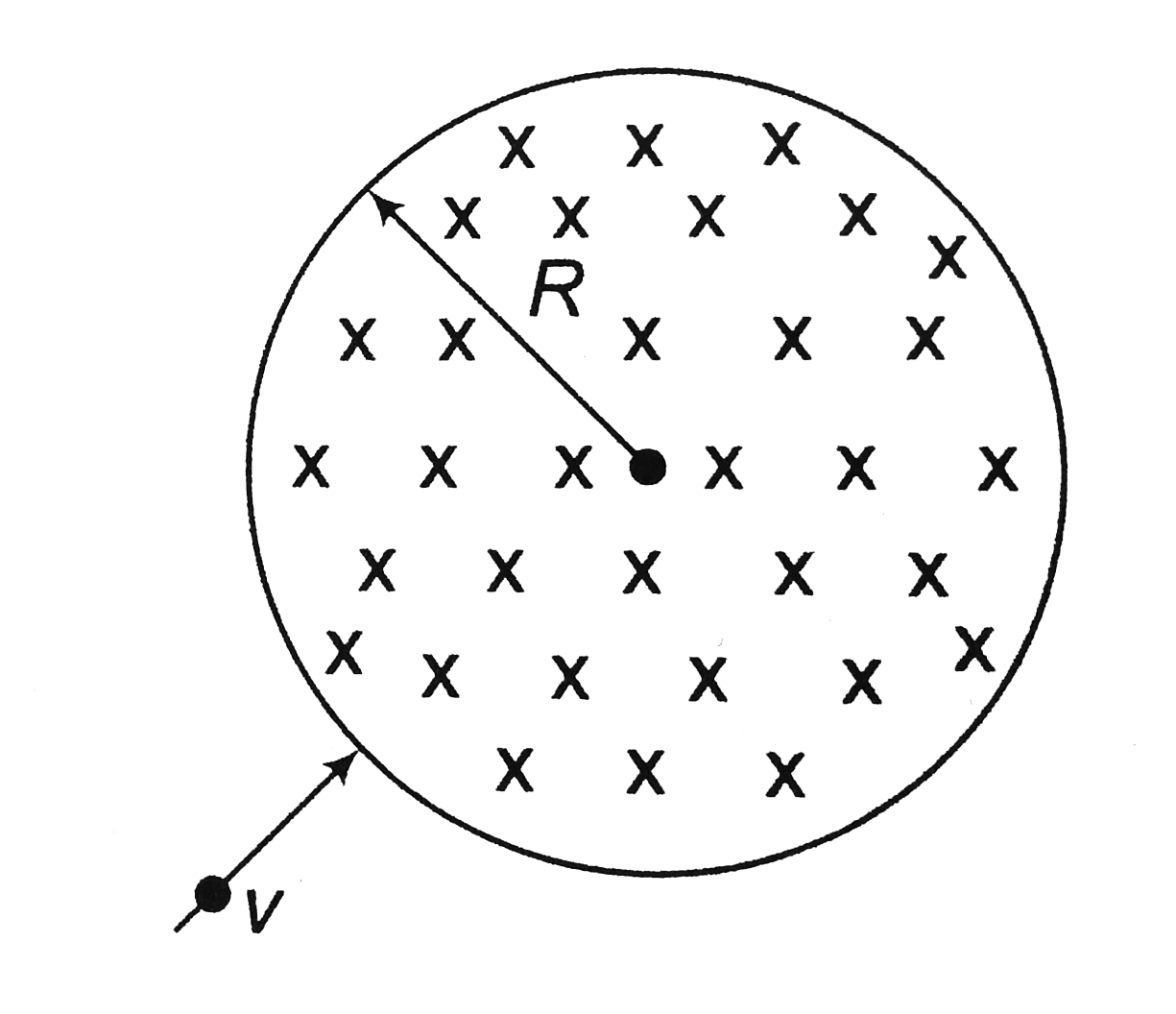
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View Solution
