A tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
μ0qrni2m
μ0qrnim
2μ0qrni3m
none of these
The correct Answer is:A
To solve the problem of finding the maximum speed vmax for which a charged particle does not strike a tightly-wound long solenoid, we can follow these steps:
Step 1: Understand the setup
The solenoid has n turns per unit length, a radius r, and carries a current i. A particle with charge q and mass m is projected from the axis of the solenoid in a direction perpendicular to the axis.
Step 2: Identify forces acting on the particle
When the charged particle moves in the magnetic field created by the solenoid, it experiences a magnetic force. This magnetic force will act as the centripetal force required to keep the particle in circular motion.
Step 3: Determine the magnetic field inside the solenoid
The magnetic field B inside a long solenoid is given by the formula:
B=μ0ni
where μ0 is the permeability of free space, n is the number of turns per unit length, and i is the current flowing through the solenoid.
Step 4: Write the expression for magnetic force
The magnetic force FB acting on the particle is given by:
FB=qvB
where v is the speed of the particle and B is the magnetic field.
Step 5: Set the magnetic force equal to the centripetal force
The centripetal force FC required to keep the particle in circular motion is given by:
FC=mv2r′
where r′ is the radius of the circular path of the particle. For the particle to not strike the solenoid, we can assume that the maximum radius of the circular path is r2 (half the radius of the solenoid).
Setting the magnetic force equal to the centripetal force gives:
qvB=mv2r2
Step 6: Substitute the expression for magnetic field
Substituting B=μ0ni into the equation gives:
qv(μ0ni)=mv2r2
Step 7: Simplify the equation
Rearranging the equation, we have:
qvμ0ni=2mv2r
Now, divide both sides by v (assuming v≠0):
qμ0ni=2mvr
Step 8: Solve for v
Rearranging gives:
v=qμ0nir2m
Conclusion
Thus, the maximum speed vmax for which the particle does not strike the solenoid is:
vmax=qμ0nir2m
The solenoid has n turns per unit length, a radius r, and carries a current i. A particle with charge q and mass m is projected from the axis of the solenoid in a direction perpendicular to the axis.
When the charged particle moves in the magnetic field created by the solenoid, it experiences a magnetic force. This magnetic force will act as the centripetal force required to keep the particle in circular motion.
The magnetic field B inside a long solenoid is given by the formula:
B=μ0ni
where μ0 is the permeability of free space, n is the number of turns per unit length, and i is the current flowing through the solenoid.
The magnetic force FB acting on the particle is given by:
FB=qvB
where v is the speed of the particle and B is the magnetic field.
The centripetal force FC required to keep the particle in circular motion is given by:
FC=mv2r′
where r′ is the radius of the circular path of the particle. For the particle to not strike the solenoid, we can assume that the maximum radius of the circular path is r2 (half the radius of the solenoid).
qvB=mv2r2
Substituting B=μ0ni into the equation gives:
qv(μ0ni)=mv2r2
Rearranging the equation, we have:
qvμ0ni=2mv2r
Now, divide both sides by v (assuming v≠0):
qμ0ni=2mvr
Rearranging gives:
v=qμ0nir2m
Thus, the maximum speed vmax for which the particle does not strike the solenoid is:
vmax=qμ0nir2m
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
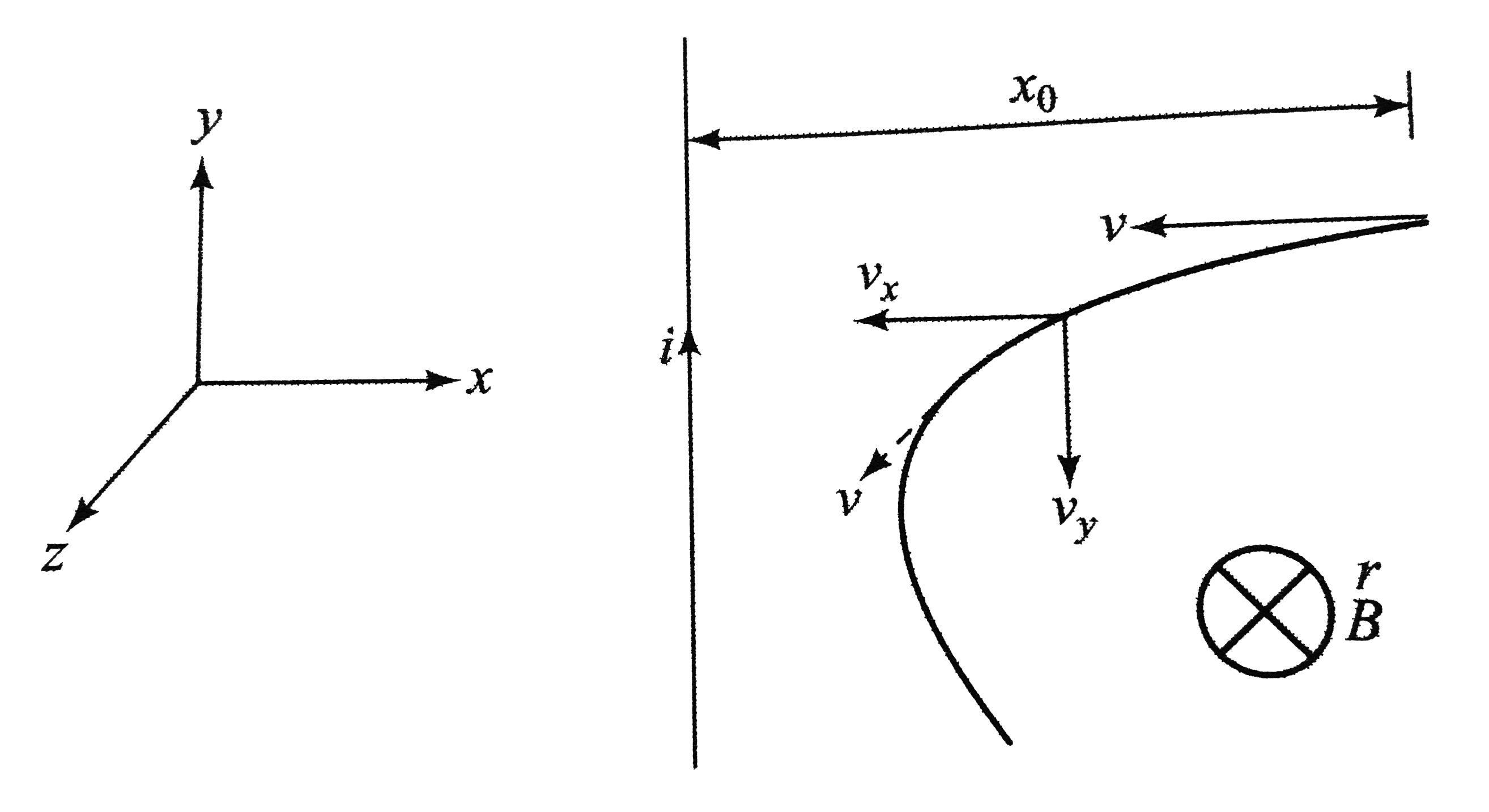
View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View SolutionConsider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
View SolutionA uniform magnetic field ¯¯¯B=B0ˆj exists in a space. A particle of mass m and charge q is projected towards negative x-axis with speed v from the a point (d,0,0) The maximum value v for which the particle does not hit y−z plane is .
View SolutionA solenoid of length 10 cm and radius 1 cm contains 200 turns and carries a current of 10 A. Find the magnetic field at a point on the axis at a distance of 10cm from the centre.
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA tightly- wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current I n dx. (a) Write the magnetic field at the center of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the center of the solenoid. (b) Verify that if l>>a, the field tends to (B=(μ0ni) and if a>>1, the field tends toB=((μ0)nil2a) . Interpret these results.
View SolutionTwo infinite long wires, each carrying current I, are lying along x- and y-axis, respectively. A charged particle, having a charge q and mass m, is projected with a velocity u along the straight line OP. The path of the particle is (neglect gravity)

View Solution
