Two points mass m and 2m are kept at a distance a. Find the speed of particles and their relative velocity of approach when separation becomes a/2.
2√3a2Gm
√a2Gm
2√2Gm3a
√6Gma
The correct Answer is:D
To solve the problem of finding the speed of the particles and their relative velocity of approach when the separation becomes a2, we can follow these steps:
Step 1: Understand the System
Initially, we have two masses m and 2m separated by a distance a. They are at rest, and since there are no external forces acting on them, the momentum of the system will be conserved.
Step 2: Set Up the Conservation of Momentum
Let v1 be the velocity of mass m and v2 be the velocity of mass 2m when the distance between them becomes a2. According to the conservation of momentum:
mv1−2mv2=0
From this equation, we can express v1 in terms of v2:
v1=2v2
Step 3: Apply Conservation of Energy
The mechanical energy of the system is conserved. Initially, the kinetic energy is zero (since both masses are at rest), and the potential energy due to gravitational attraction is given by:
Ui=−G⋅m⋅2ma=−2Gm2a
When the separation becomes a2, the potential energy is:
Uf=−G⋅m⋅2ma2=−4Gm2a
The total mechanical energy conservation can be expressed as:
Ki+Ui=Kf+Uf
Since Ki=0:
−2Gm2a=12mv21+12(2m)v22−4Gm2a
Step 4: Solve for Velocities
Rearranging the equation gives:
12mv21+mv22=2Gm2a
Substituting v1=2v2:
12m(2v2)2+mv22=2Gm2a
This simplifies to:
12m(4v22)+mv22=2Gm2a
2mv22+mv22=2Gm2a
3mv22=2Gm2a
Dividing both sides by m:
3v22=2Gma
Thus,
v22=2Gm3a
Taking the square root:
v2=√2Gm3a
Now substituting back to find v1:
v1=2v2=2√2Gm3a=√8Gm3a
Step 5: Find the Relative Velocity of Approach
The relative velocity of approach vrel is given by:
vrel=v1+v2=√8Gm3a+√2Gm3a
Finding a common term:
vrel=√2Gm3a(2+1)=3√2Gm3a
Final Result
Thus, the speed of the particles when the separation becomes a2 is:
- v1=√8Gm3a
- v2=√2Gm3a
- Relative velocity of approach vrel=3√2Gm3a
Initially, we have two masses m and 2m separated by a distance a. They are at rest, and since there are no external forces acting on them, the momentum of the system will be conserved.
Let v1 be the velocity of mass m and v2 be the velocity of mass 2m when the distance between them becomes a2. According to the conservation of momentum:
The mechanical energy of the system is conserved. Initially, the kinetic energy is zero (since both masses are at rest), and the potential energy due to gravitational attraction is given by:
Rearranging the equation gives:
The relative velocity of approach vrel is given by:
Thus, the speed of the particles when the separation becomes a2 is:
- v2=√2Gm3a
- Relative velocity of approach vrel=3√2Gm3a
Similar Questions
Two particles of mass m and M are initialljy at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when d is their separation at any instant
View SolutionTwo point particles of mass m and 2m are initially separated by a distance 4a. They are then released to become free to move. Find the velocities of both the particles when the distance between them reduces to a.
View SolutionTwo identical particles, each having a charge of 2.0×10−4C and mass of 10g, are kept at a separation of 10cm and then released. What would be the speeds of the particles when the separation becomes large?
View SolutionTwo bodies of mass m1andm2 are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attraction. Show that their relative velocity of approach at separation r between them is:
View SolutionTwo points masses 'm' and 2m are kept at certain distance as shows in figure. Draw E−r and V−r graphs along the line joining them corresponding to given mass system.

View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View SolutionStatement-1: Two particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5m/s. When the relative velocity of approach becomes 3m/s the velocity of the centre of mass is 0.75m/s.
Statement-2: The total kinetic energy as seen from ground is 12μv2rel+12mv2c and in absence of external force, total energy remains conserved.
View Solution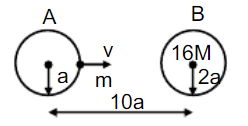
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View SolutionTwo point masses m1 and m2 at rest in gravity free space are released from distance d. Find the velocity of the CM of the system at the time of collision of particles
View Solution

