Two points mass m and 2m are kept at a distance a. Find the speed of particles and their relative velocity of approach when separation becomes a/2.
Reduced mass μ=m.2mm+2m=2m3
Changining in potential energy is
U1−U2=−Gm.2ma−(−Gm.2ma/2)
=2Gm2a
12μv21/2=2Gm2a⇒12=√6Gma
v1/2=v1+v2=√6Gma ......(i)
mv1=2mv2
v1=2v2
v1+v2=3v2=√6Gma⇒v2=13√6Gma=√2Gm3a
v1=2v2=2aqrt(2Gm3a)
Topper's Solved these Questions
Similar Questions
Two particle of mass m and M are initially at rest at inifinte distance . Find their relative velocity of approch due to grvitational atraction when d is their separation at any instant . [Hint : From the principle of conservation of energy GmMd=12mv21+12v22. . From the principle of conservationl of momentum , mv1−Mv2=0 . Relative velocity of approch =V1+V2]
View SolutionTwo particles m1 and m2 are initially at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when their separation is d.
View Solution
Knowledge Check
Two particles of mass m and M are initialljy at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when d is their separation at any instant
A√2G(M+m)dB√G(M+m)dC√G(M+m)2dD√G(M+m)4dTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)
Two point particles of mass m and 2m are initially separated by a distance 4a. They are then released to become free to move. Find the velocities of both the particles when the distance between them reduces to a.
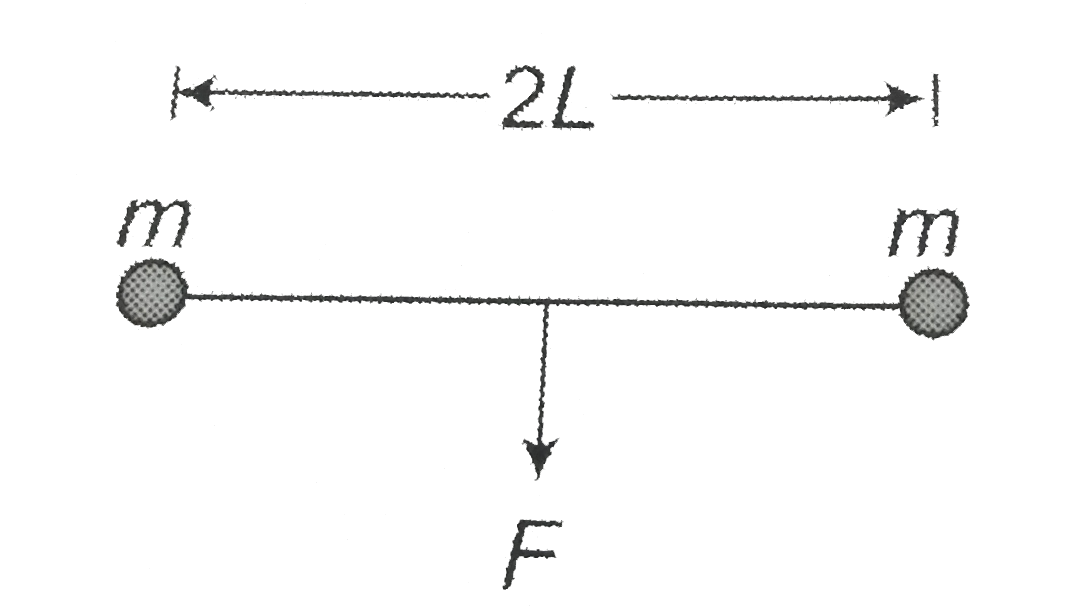
View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
View SolutionTwo bodies of masses m and 2m are kept at distance r apart from each other. Then the value of G varies as
View SolutionTwo charged particles having charge 1μC and −μC and of mass 50gm each are held ar rest while their separtion is 2m. Find the relative velocity of the particles when their separation is 0.5m.
View SolutionTwo particles of mass m and M are initially at rest and infinitely separated from each other. Due to mutual interaction, they approach each other.
Their relative velocity of approach at a separation d between them, is
View Solution
