A circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
To determine the magnetic moment of a circular loop of wire of radius R that is bent about its diameter along two mutually perpendicular planes, we can follow these steps:
Step 1: Understand the Configuration
The loop is bent in two perpendicular planes, which means we can consider the magnetic moments generated in each plane separately. The current I flows through the loop.
Step 2: Calculate the Area of the Loop
The area A of a circular loop is given by the formula:
A=πR2
Step 3: Determine the Magnetic Moment for Each Plane
The magnetic moment M for a loop carrying current I is given by:
M=I×A
For the first plane (let's say the XY-plane):
The magnetic moment M1 can be calculated as:
M1=I×A=I×πR2^j
where ^j indicates the direction of the magnetic moment in the Y-axis.
For the second plane (the XZ-plane):
The magnetic moment M2 can be calculated similarly:
M2=I×A=I×πR2^i
where ^i indicates the direction of the magnetic moment in the X-axis.
Step 4: Combine the Magnetic Moments
The total magnetic moment M of the loop can be found by adding the contributions from both planes:
M=M1+M2=IπR2^j+IπR2^i
This can be simplified to:
M=IπR2(^i+^j)
Final Answer
The total magnetic moment of the loop is:
M=IπR2(^i+^j)
---
The loop is bent in two perpendicular planes, which means we can consider the magnetic moments generated in each plane separately. The current I flows through the loop.
The area A of a circular loop is given by the formula:
A=πR2
The magnetic moment M for a loop carrying current I is given by:
M=I×A
The magnetic moment M1 can be calculated as:
M1=I×A=I×πR2^j
where ^j indicates the direction of the magnetic moment in the Y-axis.
The magnetic moment M2 can be calculated similarly:
M2=I×A=I×πR2^i
where ^i indicates the direction of the magnetic moment in the X-axis.
The total magnetic moment M of the loop can be found by adding the contributions from both planes:
M=M1+M2=IπR2^j+IπR2^i
This can be simplified to:
M=IπR2(^i+^j)
The total magnetic moment of the loop is:
M=IπR2(^i+^j)
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionA circular coil of Radius R is folded across its diameter such that the planes of two half rings are perpendicular to each other as shown in the figure. If the current through the coil is calculate the magnetic dipole moment of the configuration so formed.
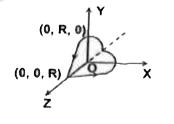
View SolutionA conductor consists of a circular loop of radius R=10cm and two straight, long sections as shown in figure. The wire lies in the plane of the paper and carries a current of i=7.00A Determine the magnitude and direction of the magnetic field at the centre of the loop.

View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionTwo infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View Solution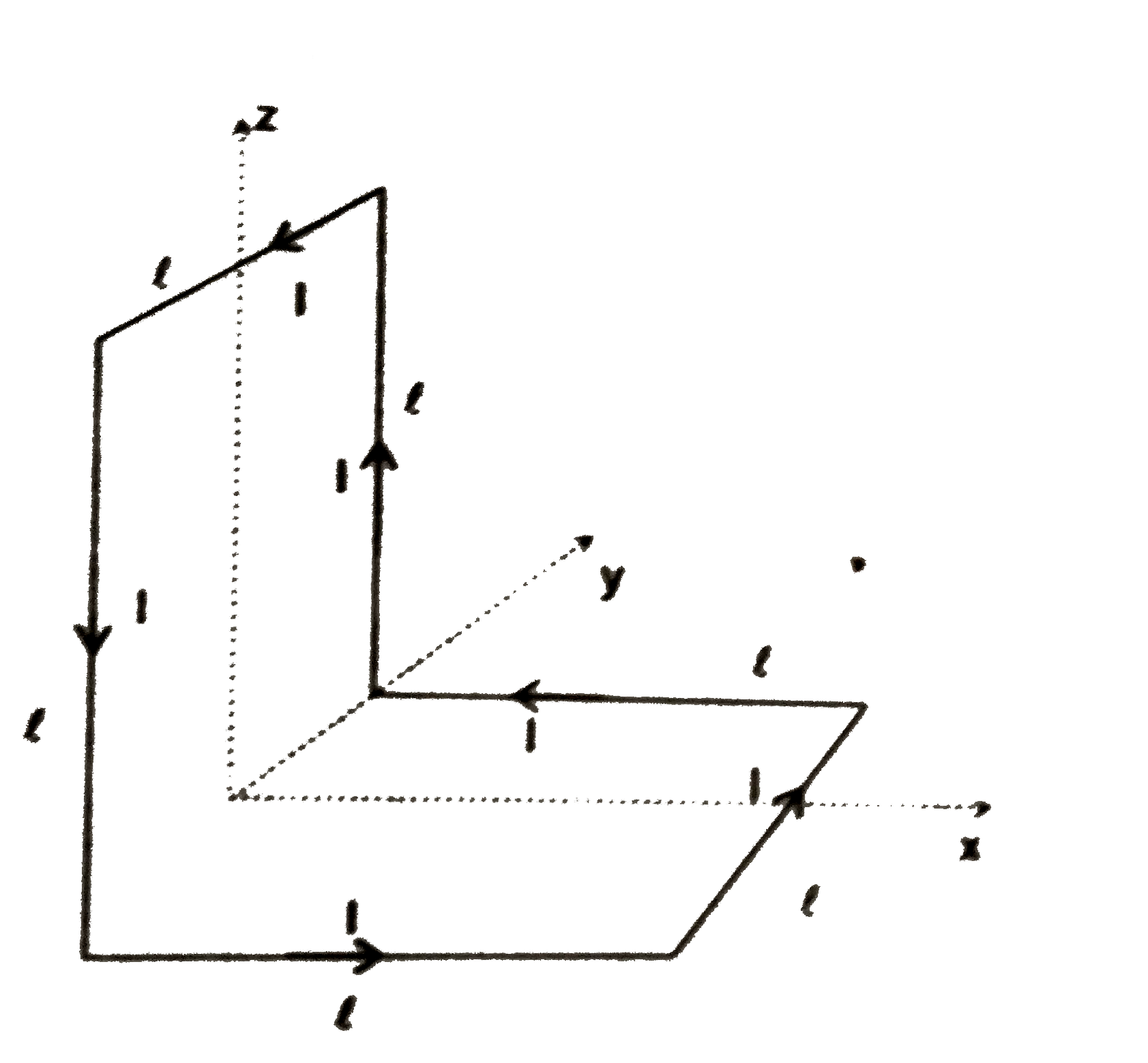
A conducting loop carrying current 'l' is bent into two halves and placed in mutually perpendicular planes xy and yz planes as shown. A uniform magnetic field →B=Bˆj is existing in the region. The net magnetic torque experienced by the loop is
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
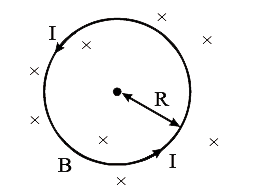
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View Solution
