A circular loop of radius R is bent along a diameter and given a shapes as shown in the figure. One of the semicircles (KNM) lies in the x−z plane with their centres and the other one (KLM) in the y−z plane with their centres at the origin. current I is flowing through each of the semi circles as shown in figure.
(a) A particle of charge q is released at the origin with a velocity →v=−v0ˆi. Find the instantaneous force →F on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied , determine the force →F1and→F2 on the semicircles KLMandKNM due to the field and the net force →F on the loop.
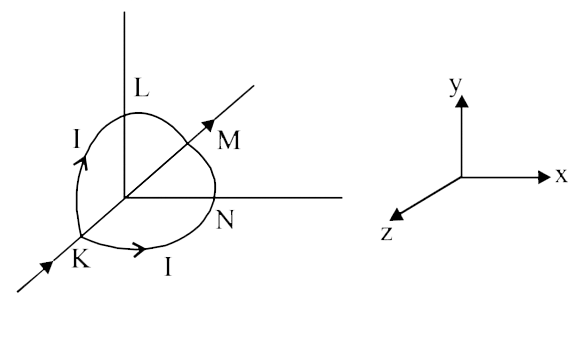
R=Radius of circular loop. Given that semicircle KNM lies
in the x-z plane while the semicircle KLM lies in the y-z plane.
Both the semicircle have their centres located at the origin.
(a) Charge on the particle released at the origin=q
Velocity of the particle, →v=−v0ˆi
Magnetic field at centre O due to current carrying loop
KLM lying in y-z plane, →B2=μ0I4R(ˆj).
Thus, the two fields at O are mutually perpendicular in
vector form. Total field at O can be expressed as
→B=−ˆiB1+ˆjB2=μ0I4R(−ˆi+ˆj)


Hence, instantaneous force acting on the charged particle.
released at O.


→F=q(→v×→B)=q[−v0ˆi×(−ˆi+ˆj)μ0I4R]
=qμ0Iv04R[ˆi×(ˆi−ˆj)]=−qμ0Iv04Rˆk,
(b) External uniform magnetic field →Bext=Bˆj
As semicircular wires are placed in uniform magnetic field,
these loops can be reduced to straight wires each of length
2R placed along z-axis (by joining initial point K and final
point M).
→FKLM=→FKMN=→FKM=BI2Rˆi
Net force due to both the wires:
→F=→FKLM+→FKMN=4BIRˆi
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.1
Explore 35 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.2
Explore 10 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
A circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30,A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure.
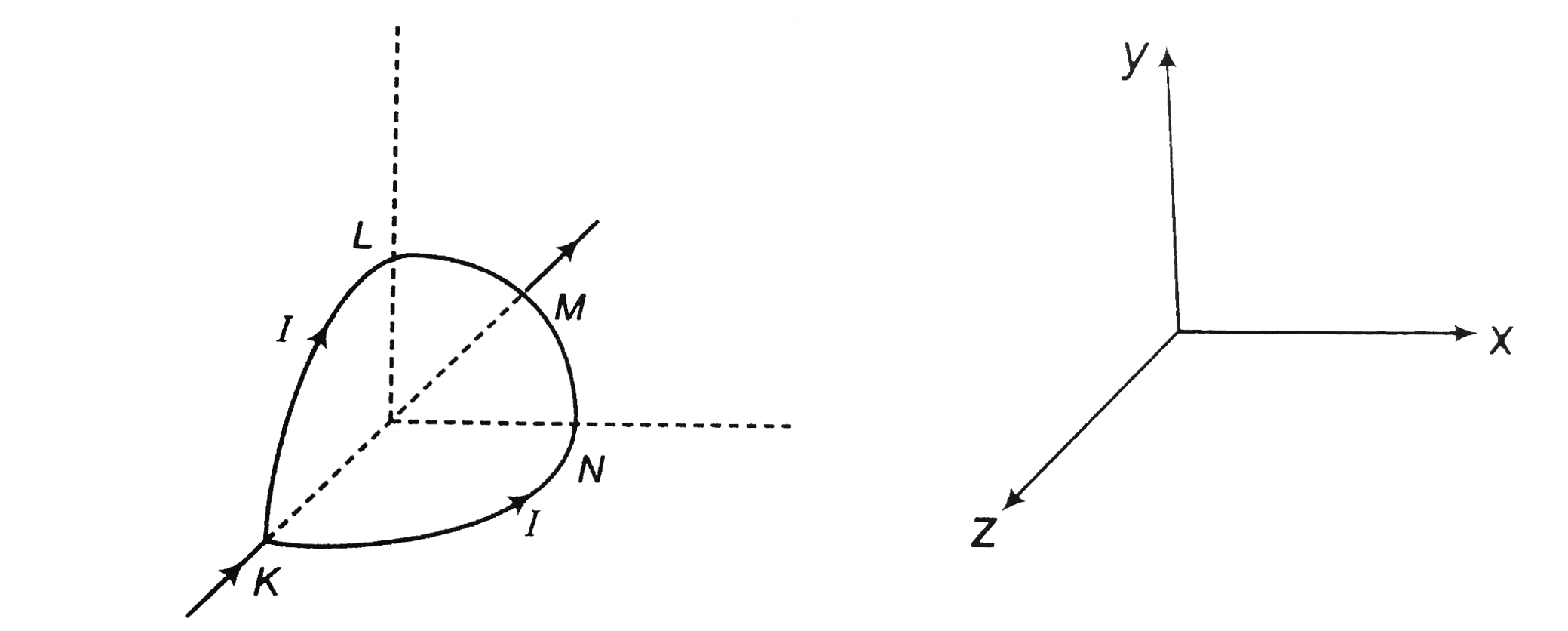
(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
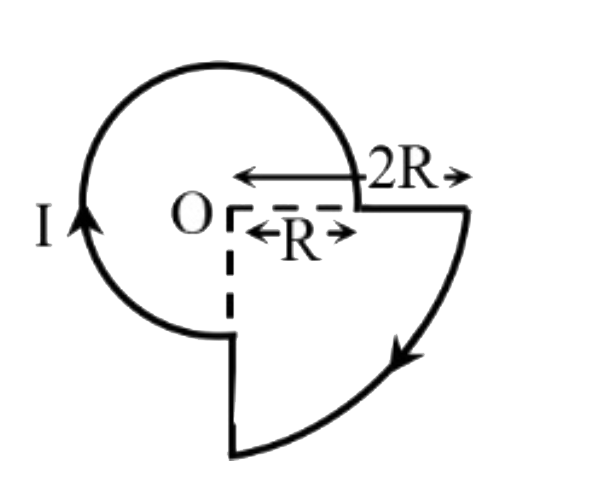
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
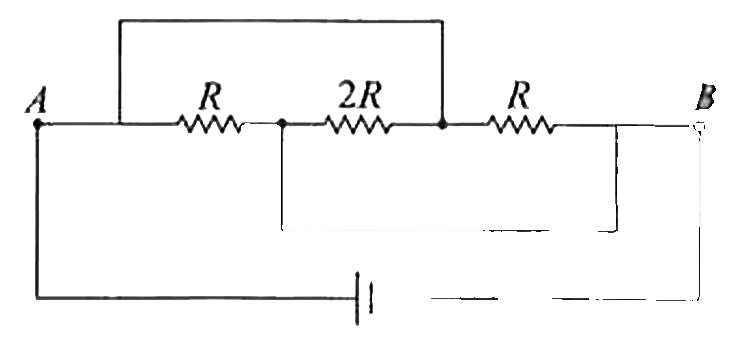
View SolutionIn the figure shown the current flowing through 2R is:
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
View SolutionA circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
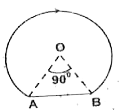
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

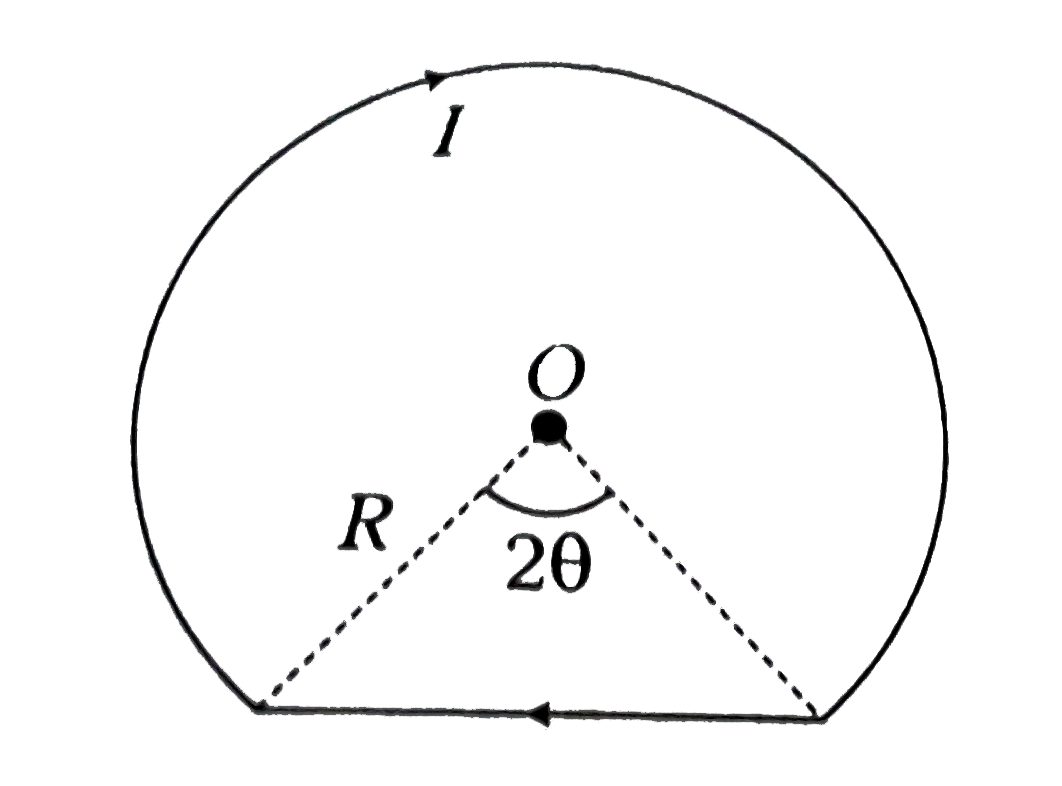
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionA loop is kept so that its center lies at the origin of the pointing along Z -axis as shown in the figure
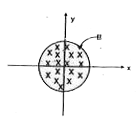
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View Solution
