A long straight wire is coplanar with a current carrying circular loop of radius R as shown in Fig. Current flowing through wire and the loop is and I, respectively. If distance between centre of loop and wire is calculate force of attraction between the wire and the loop.

Consider two equal elemental
arc length MN and M'N' of lengths
. The distance of each elemental
length from straight wire is
The magnetic induction at these
elemental arc lengths due to current
in the wire is by
The magnitude of the force on each elemental length
The direction of dF' is shown in Fig.

The resultant force dF is given by
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.1
Explore 35 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.2
Explore 10 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
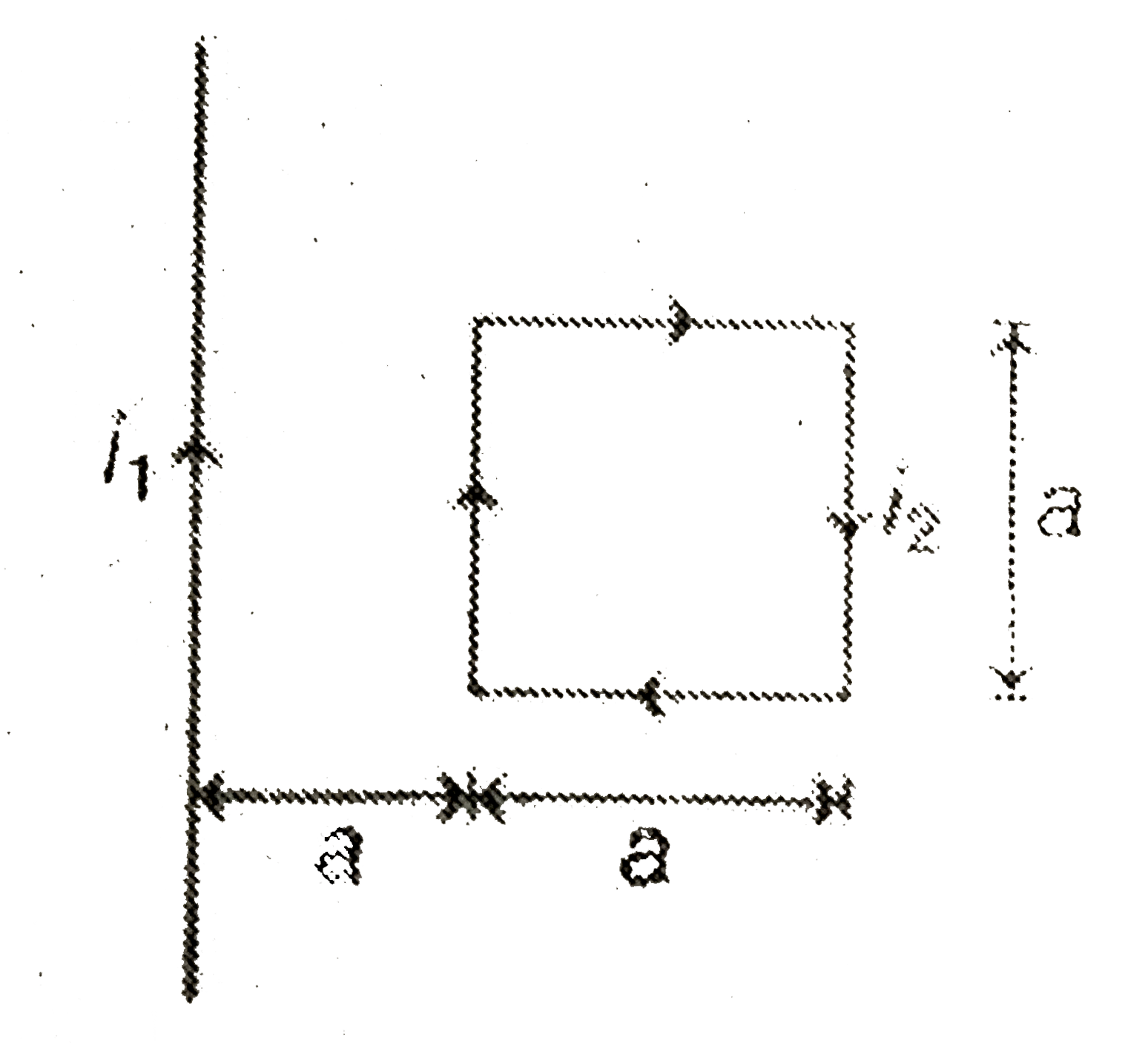
A current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionAn equilateral triangular loop is kept near to a current carrying long wire as shown fig. under the action of magnetic force alone, the loop

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionA current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
View SolutionA current carrying straight wire passing inside a triangular loop as shown in Figure. The current in the wire is perpendicular to paper inwards. Find the direction of the induced current in the loop if current in the wire is increased.

View SolutionA triangular loop (ABC) having current i2 and an infinite wire having current i1 are placed in the same plane.Find the magnetic force of interaction between the infinite wire and the loop ABC.

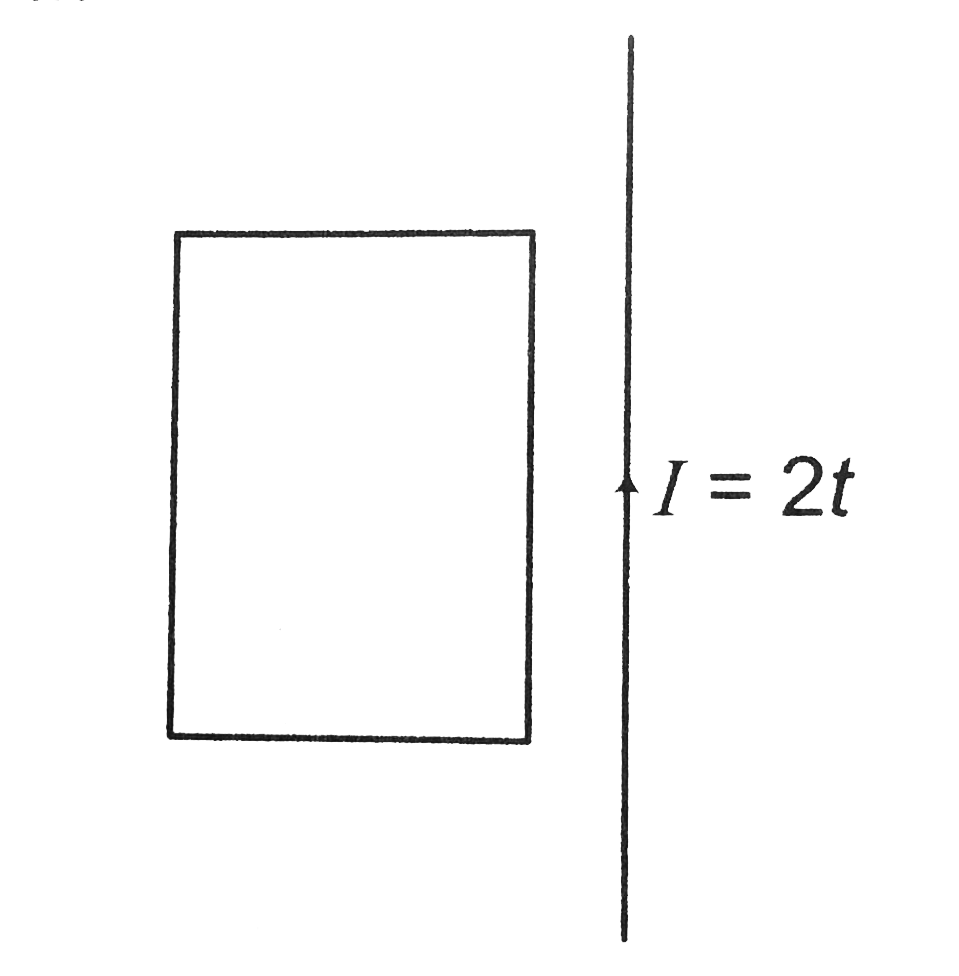
View SolutionA rectangular loop is placed to the left of large current carrying straight wire as shown in Figure. Current varies with time as I=2t. Find direction of induced current Iin in the square loop.
View SolutionAn infinitely long straight wire carrying a current I1 is partially surrounded by a loop as shown in Fig. The loop has a length L, radius R, and carries a current I2 The axis of the loop coincides with the wire. Calculate the force exerted on the loop.

View Solution
