From the surface of a round wire of radius a carrying a direct current i, a positive charge q escapes with a velocity v0 perpendicular to the surface. Find what the maximum distance of the electron will be from the axis of the wire before it turns back due to the action of the magnetic field generated by the current.
To solve the problem of finding the maximum distance X of a positive charge q escaping from a round wire of radius a carrying a direct current I, we can follow these steps:
Step 1: Understand the Situation
We have a round wire with radius a carrying a current I. A positive charge q escapes from the surface of the wire with an initial velocity v0 perpendicular to the surface. The current in the wire generates a magnetic field around it.
Step 2: Determine the Direction of the Magnetic Field
Using the right-hand rule, we can determine the direction of the magnetic field B around the wire. For a straight wire carrying current I in the positive z-direction, the magnetic field at a distance x from the wire is given by:
B=μ0I2πx
where μ0 is the permeability of free space.
Step 3: Analyze the Force on the Charge
The force F acting on the charge q due to the magnetic field is given by the Lorentz force law:
F=qv×B
Since the velocity v of the charge is perpendicular to the magnetic field B, the force will act perpendicular to both v and B.
Step 4: Write the Expression for the Force
Assuming the charge moves in the x-z plane, we can express the velocity as:
v=vx^i+vz^k
The magnetic field B at distance x is in the y-direction:
B=B^j=μ0I2πx^j
Thus, the force can be expressed as:
F=q(vx^i+vz^k)×(μ0I2πx^j)
Calculating the cross product gives:
F=qμ0I2πx(vz^i−vx^k)
Step 5: Write the Equations of Motion
The acceleration a in the x-direction can be expressed as:
ax=Fxm=qμ0I2πmxvz
Using the relationship a=vdvdx, we can write:
vxdvxdx=qμ0I2πmxvz
Step 6: Relate Velocities
Using the conservation of energy, we have:
v20=v2x+v2z⇒vz=√v20−v2x
Step 7: Substitute and Integrate
Substituting vz into the equation gives:
vxdvxdx=qμ0I2πmx√v20−v2x
Rearranging and separating variables leads to:
vx√v20−v2xdvx=qμ0I2πm1xdx
Integrating both sides from a to X and from v0 to 0.
Step 8: Solve the Integrals
After performing the integration, we find:
ln(Xa)=−2πmv0qμ0I
Thus, solving for X:
X=ae−2πmv0qμ0I
Final Result
The maximum distance X of the charge from the axis of the wire before it turns back is given by:
X=ae2πmv0qμ0I
We have a round wire with radius a carrying a current I. A positive charge q escapes from the surface of the wire with an initial velocity v0 perpendicular to the surface. The current in the wire generates a magnetic field around it.
Using the right-hand rule, we can determine the direction of the magnetic field B around the wire. For a straight wire carrying current I in the positive z-direction, the magnetic field at a distance x from the wire is given by:
B=μ0I2πx
where μ0 is the permeability of free space.
The force F acting on the charge q due to the magnetic field is given by the Lorentz force law:
F=qv×B
Since the velocity v of the charge is perpendicular to the magnetic field B, the force will act perpendicular to both v and B.
Assuming the charge moves in the x-z plane, we can express the velocity as:
v=vx^i+vz^k
The magnetic field B at distance x is in the y-direction:
B=B^j=μ0I2πx^j
Thus, the force can be expressed as:
F=q(vx^i+vz^k)×(μ0I2πx^j)
Calculating the cross product gives:
F=qμ0I2πx(vz^i−vx^k)
The acceleration a in the x-direction can be expressed as:
ax=Fxm=qμ0I2πmxvz
Using the relationship a=vdvdx, we can write:
vxdvxdx=qμ0I2πmxvz
Using the conservation of energy, we have:
v20=v2x+v2z⇒vz=√v20−v2x
Substituting vz into the equation gives:
vxdvxdx=qμ0I2πmx√v20−v2x
Rearranging and separating variables leads to:
vx√v20−v2xdvx=qμ0I2πm1xdx
Integrating both sides from a to X and from v0 to 0.
After performing the integration, we find:
ln(Xa)=−2πmv0qμ0I
Thus, solving for X:
X=ae−2πmv0qμ0I
The maximum distance X of the charge from the axis of the wire before it turns back is given by:
X=ae2πmv0qμ0I
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
An electric current flows in a wire from north to south.
What will be the direction of the magnetic field due to this wire at a point.
View SolutionMagnetic field exist in the space and given as →B=−B0l2x2ˆk, where B0and l positive constants. A particle having positive charge 'q' and mass 'm' is pojected wit speed 'v0' along positive x axis from the origin. What is the maimum distance of the charged particle from the y-axis before it turns back due to the magnetic field. (Ignore any interaction other than magnetic field)
View SolutionA semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance in the wire when its distance from the long wire is x.
View SolutionA long straight wire of radius 10mm carries a current uniformly distributed over its cross section. The ration of magnetic fields due to the wire at distance of 5mm and 15 mm, respectively from the axis of the wire is
View SolutionA long straight wire of radius 10mm carries a current uniformly distributed over its cross section. The ration of magnetic fields due to the wire at distance of 5mm and 15 mm, respectively from the axis of the wire is
View SolutionAn electron is ejected from the surface of a long, thick straight conductor carrying a current, initially in a direction perpendicular to the conductor. The electron will
View Solution(i) A very long wire carrying a current I is bent at right angles .Find magnetic field at a point lying on a perpendicular to the wire , drawn through the point of bending at a distance d from it
(ii) Three long wires carrying same currect are placed as shown Find magnetic field at O.
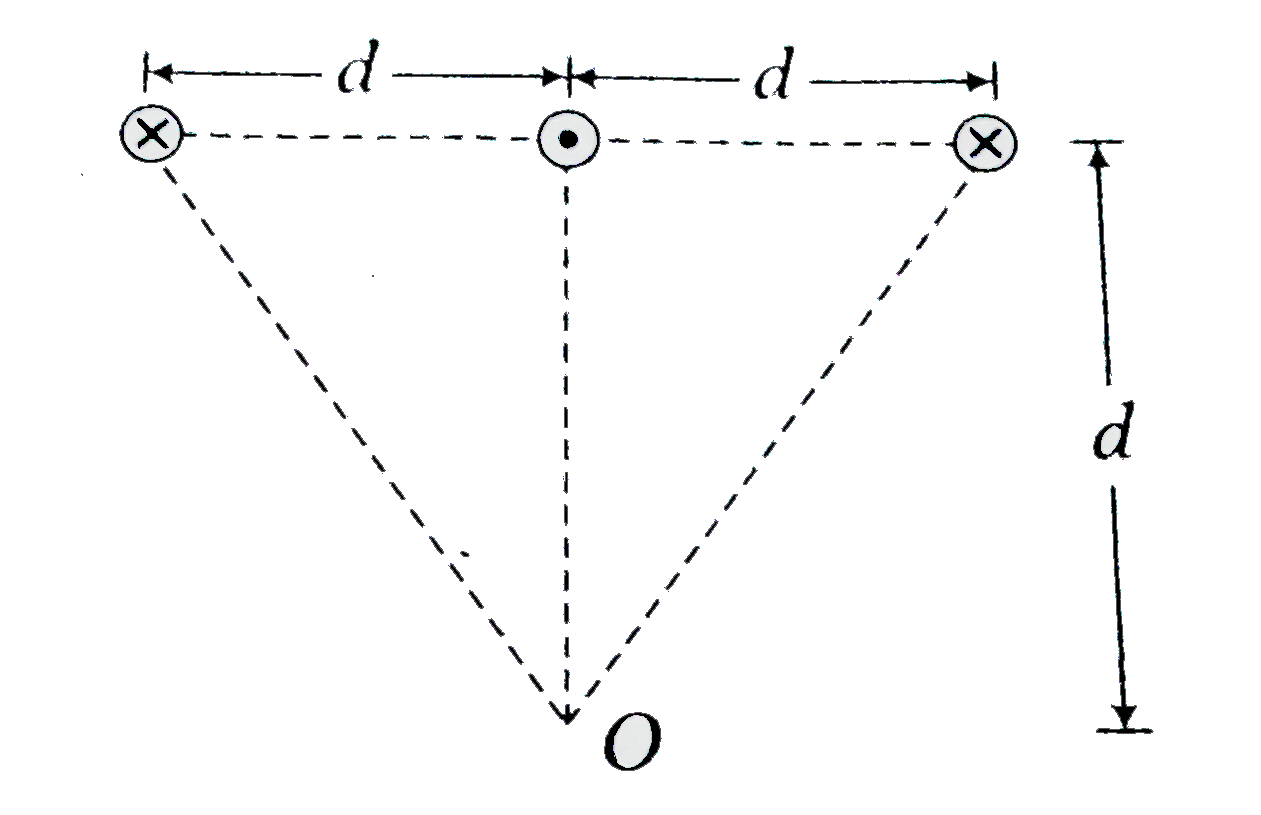
View SolutionA copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (vec B)due to this current.
View Solution
