Three infinitely long thin wires, each carrying current i in the same dieretion, are the xy plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d
i find the locus of the points for which the magnetic field B is zero.
ii If the central wire is displaced along the z-direction by a small amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is λ, find the frequency of oscillation.
(a) Magnetic field will be zero on the y-axis i.e.,
x=0=z

magnetic fild cannot be zero in region I and region IV bec-
ause in region I magnetic field is along positive z-direction
due to all the three wires, while in region IV magnetic field
is along negative z-axis due to all the three wires. It can be
zero only in region II and III.

Let magnetic fild be zero on line (z=0)andx=x. Then
magnetic fild on this line due to wires (1) and (2) will be
along negative z-axis and due to wire (3) along positive
z-axis. Thus,
B1+B2=B3
or μ02πid+x+μ02πix=μ02πid−x
or 1d+x+1x=1d−x
This equation gives x±d√3 where magnetic field is
zero.
(b) In this part we change our coordinate axes system just for
butter understanding.

There are three wires (1),(2) and (3) as shown Fig.
If we displace wire (2) toward the z-axis, then force of
attraction per unit length between wires (1 and 2) and (2
and 3) will be given by

F=μ02πi2r
The component of F along x-axis will be cancelled out.
Net resultant force will be towards negative z-axis (or mean
position) and will be given by
Fnet=μ02πi2r(2cosθ)=2{μ02πi2r}zr=μ0πi2z2+d2z
If z<<d,thenZ2+d2=d2andFnet=−(μ0πi2d2).z
Negative sign implies that Fnet is restoring in nature
Therefore, Fnet∝−z
i.e., the wire will oscillate simple harmonically.
Let a be the acceleration of wire in this position and λ is
the mass per unit length of this wire then
Fnet=λ.a=−(μ0πi2d2).zora=−(μ0i2πλd2).za
Therefore, frequency of oscillation
f=12π√az=12πid√μ0πλ=f=i2πd√μ0πλ
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Three infinitely long thin wires each carrying current I in the same direction are in x−y plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d. If the central wire is slightly displaced along z-axis and released, show that it will execute S.H.M. The linear mass density of the wire is λ. If the time period of this small oscillation is kπdI√πλμ0, then find the value of k.
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
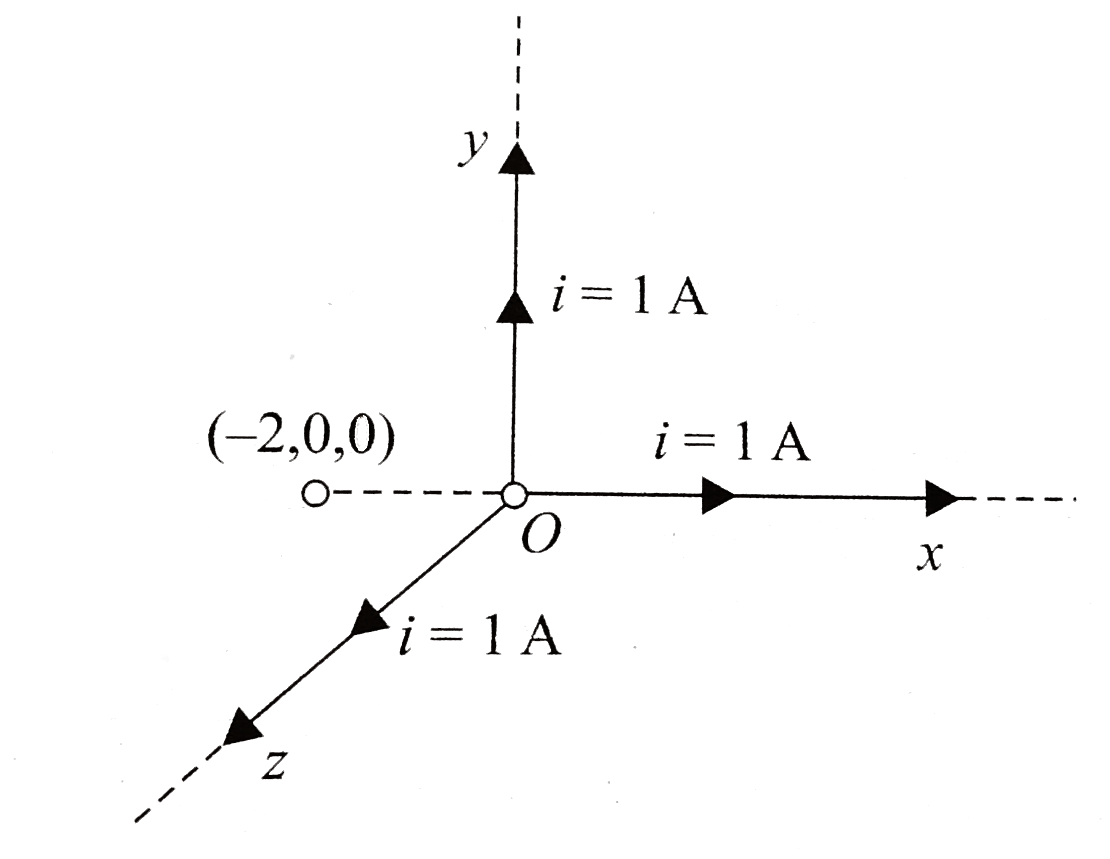
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View Solutiontwo infinite wires, carrying currents i1andi2., are lying along x-and y-axes, as shown in the x-y plane. Then,
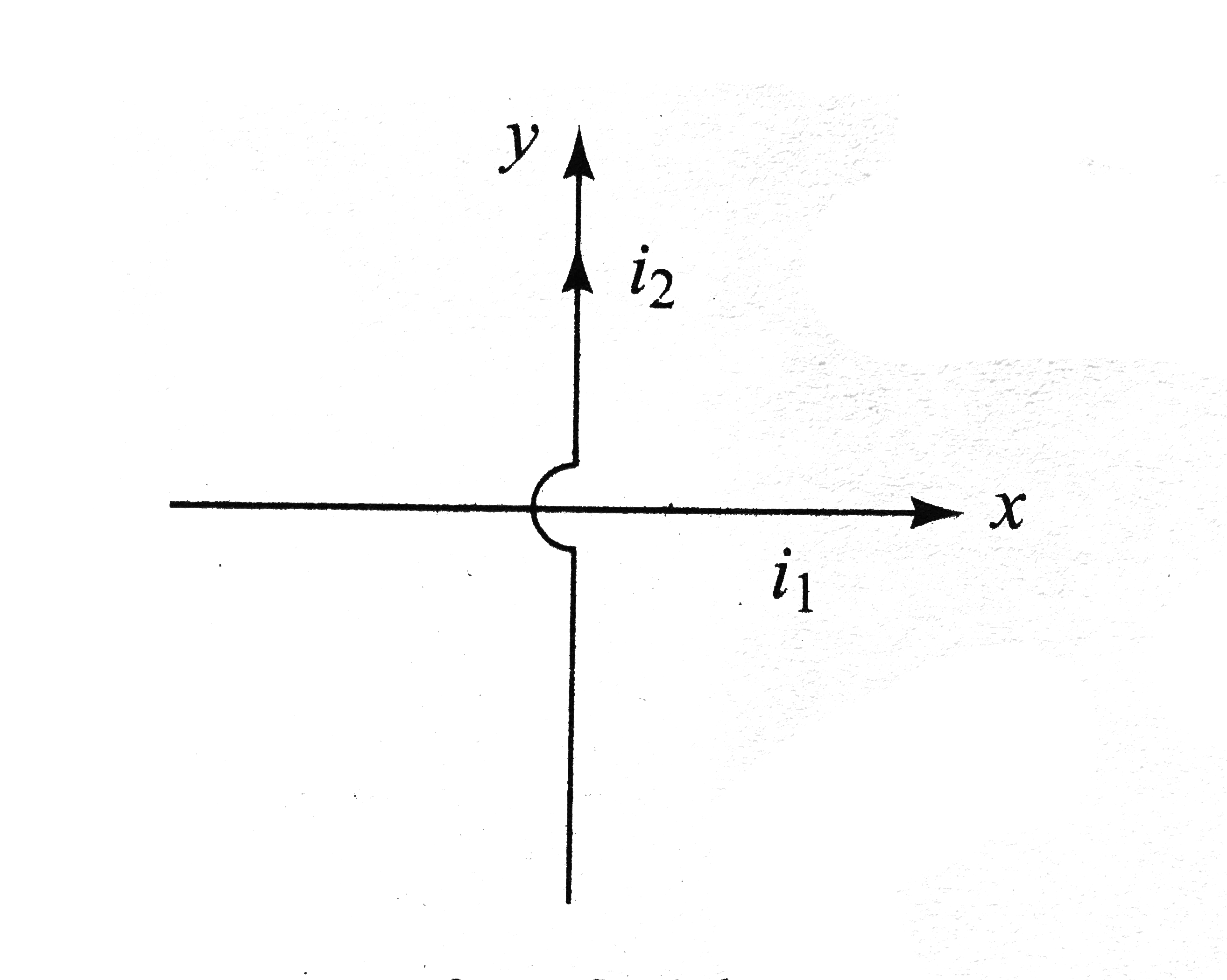
View SolutionThree coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View SolutionA long straight wire is carrying current I in + z direction .The x-y plane contains a closed circular loop carrying current I2 and not encircling the straight wire.The force on the loop will be
View Solution
