Three infinitely long thin wires each carrying current I in the same direction are in x−y plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d. If the central wire is slightly displaced along z-axis and released, show that it will execute S.H.M. The linear mass density of the wire is λ. If the time period of this small oscillation is kπdI√πλμ0, then find the value of k.
To solve the problem, we need to analyze the forces acting on the central wire when it is displaced along the z-axis and show that it executes simple harmonic motion (SHM). We will also derive the expression for the time period of the oscillation and find the value of k.
1. Understanding the Setup:
- We have three infinitely long wires carrying current I in the same direction.
- The central wire is along the y-axis, while the other two wires are at x=+d and x=−d.
- The central wire is displaced slightly along the z-axis.
2. Force Between Wires:
- The force per unit length between two parallel wires carrying currents I1 and I2 is given by:
F=μ0I1I22πr
- Here, r is the distance between the wires. For the central wire and one of the outer wires, this distance can be expressed as:
r=√d2+z2
- Since z is small compared to d, we can approximate r as d for small displacements.
3. Calculating the Force on the Central Wire:
- The force acting on the central wire due to one of the outer wires is:
F0=μ0I22πd
- The total force acting on the central wire due to both outer wires (since they are symmetrically placed) will be:
Fnet=2F0=μ0I2πd
4. Direction of the Force:
- The force acts towards the center wire when it is displaced. The net force can be expressed in terms of the displacement z:
Fnet≈−kz
- Here, k is the effective spring constant.
5. Finding the Spring Constant k:
- The effective spring constant can be derived from the force expression:
k=μ0I2πd2
6. Mass of the Central Wire:
- The linear mass density of the wire is given as λ. Therefore, the mass m of a segment of length l of the wire is:
m=λl
7. Time Period of Oscillation:
- The time period T of a simple harmonic oscillator is given by:
T=2π√mk
- Substituting m and k:
T=2π
⎷λlμ0I2πd2
- Simplifying this expression gives:
T=2π√λπd2lμ0I2
8. Final Expression for Time Period:
- If we consider l=1 (for unit length), we can express the time period as:
T=2πd√λπμ0I2
- Comparing this with the given expression T=kπdI√πλμ0, we find that k=2.
Conclusion:
The value of k is 2.
- We have three infinitely long wires carrying current I in the same direction.
- The central wire is along the y-axis, while the other two wires are at x=+d and x=−d.
- The central wire is displaced slightly along the z-axis.
- The force per unit length between two parallel wires carrying currents I1 and I2 is given by:
F=μ0I1I22πr
- Here, r is the distance between the wires. For the central wire and one of the outer wires, this distance can be expressed as:
r=√d2+z2
- Since z is small compared to d, we can approximate r as d for small displacements.
- The force acting on the central wire due to one of the outer wires is:
F0=μ0I22πd
- The total force acting on the central wire due to both outer wires (since they are symmetrically placed) will be:
Fnet=2F0=μ0I2πd
- The force acts towards the center wire when it is displaced. The net force can be expressed in terms of the displacement z:
Fnet≈−kz
- Here, k is the effective spring constant.
- The effective spring constant can be derived from the force expression:
k=μ0I2πd2
- The linear mass density of the wire is given as λ. Therefore, the mass m of a segment of length l of the wire is:
m=λl
- The time period T of a simple harmonic oscillator is given by:
T=2π√mk
- Substituting m and k:
T=2π
⎷λlμ0I2πd2
- Simplifying this expression gives:
T=2π√λπd2lμ0I2
- If we consider l=1 (for unit length), we can express the time period as:
T=2πd√λπμ0I2
- Comparing this with the given expression T=kπdI√πλμ0, we find that k=2.
The value of k is 2.
Similar Questions
Three long wires are placed in xy plane in a gravity free space. 'I' is the current flowing in each wire. The currents are constant in magnitude. Distance between each wire is 'd' and lamda is the mass per unit length of each wire. Wires 'A' and wire 'C' are fixed and wire 'B' is slightly displaced along 'z' axis. The period of oscillation of wire 'B' is
07:19View Solutionतीन अनन्त लम्बे पतले तार, जिनमें से प्रत्येक में धारा । एक ही दिशा में बह रही है, गुरुत्व मुक्त स्थान में - तल में स्थित हैं। बीच का तार Y-अक्ष के अनुदिश है जबकि अन्य दो x = d के अनुदिश हैं।
(a) ऐसे बिन्दुओं का बिन्दु पथ ज्ञात कीजिए, जहाँ चुम्बकीय क्षेत्र B शून्य हो।
(b) यदि बीच के तार को 7-अक्ष की दिशा में थोड़ा-सा विस्थापित करके छोड़ दिया जाये तो दिखाइये कि यह सरल आवर्त गति करेगा, यदि तारों का रैखिक घनत्व (Linear density)λ है, तो स्पंदन की आवृत्ति क्या है? (1997,5M)19:19View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
03:44View Solution3 Parallel thin wires of infinite length each of which I current is flowing in the same direction. xy-is placed in the floor. In the gravity-free zone, the central wire is on the y-axis and two others x = pmd Going through Suppose gravity is absent. If the central wire is left slightly displaced towards the 2-axis, if the linear density is. Then find the frequency of its oscillation.
11:40View SolutionThree infinitely long thin wires, each carrying current i in the same dieretion, are the xy plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d
i find the locus of the points for which the magnetic field B is zero.
ii If the central wire is displaced along the z-direction by a small amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is λ, find the frequency of oscillation.09:10View SolutionThree long wires are placed in xy plane in a gravity free space. 'I' is the current flowing in each wire. The currents are constant in magnitude. Distance between each wire is 'd' and λ is the mass per unit length of each wire. Wires 'A' and wire 'C' are fixed and wire 'B' is slightly displaced along 'z' axis. The period of oscillation of wire 'B' is
 08:24View Solution
08:24View SolutionAn infinite current-carrying conductor is placed along the z-axis and a wire loop is kept in the x−y plane. The current in the conductor is increasing with time. Then the
02:35View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
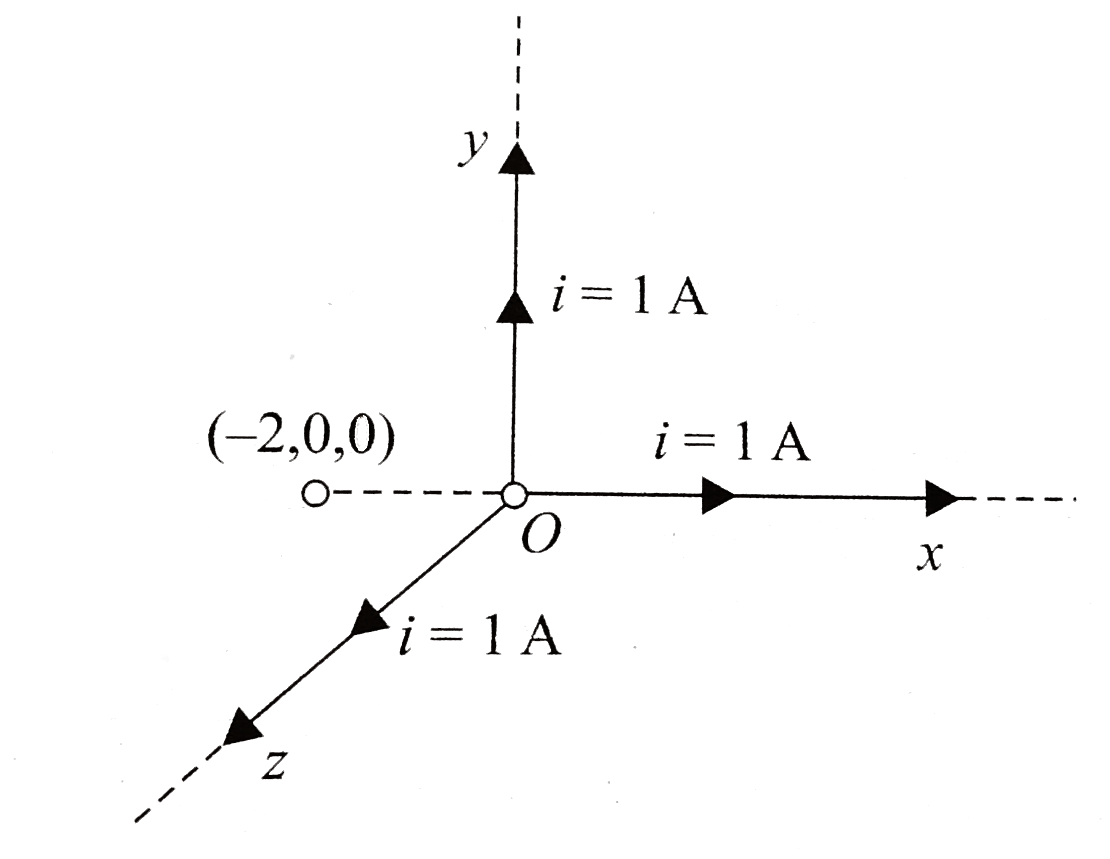 05:39View Solution
05:39View Solution
