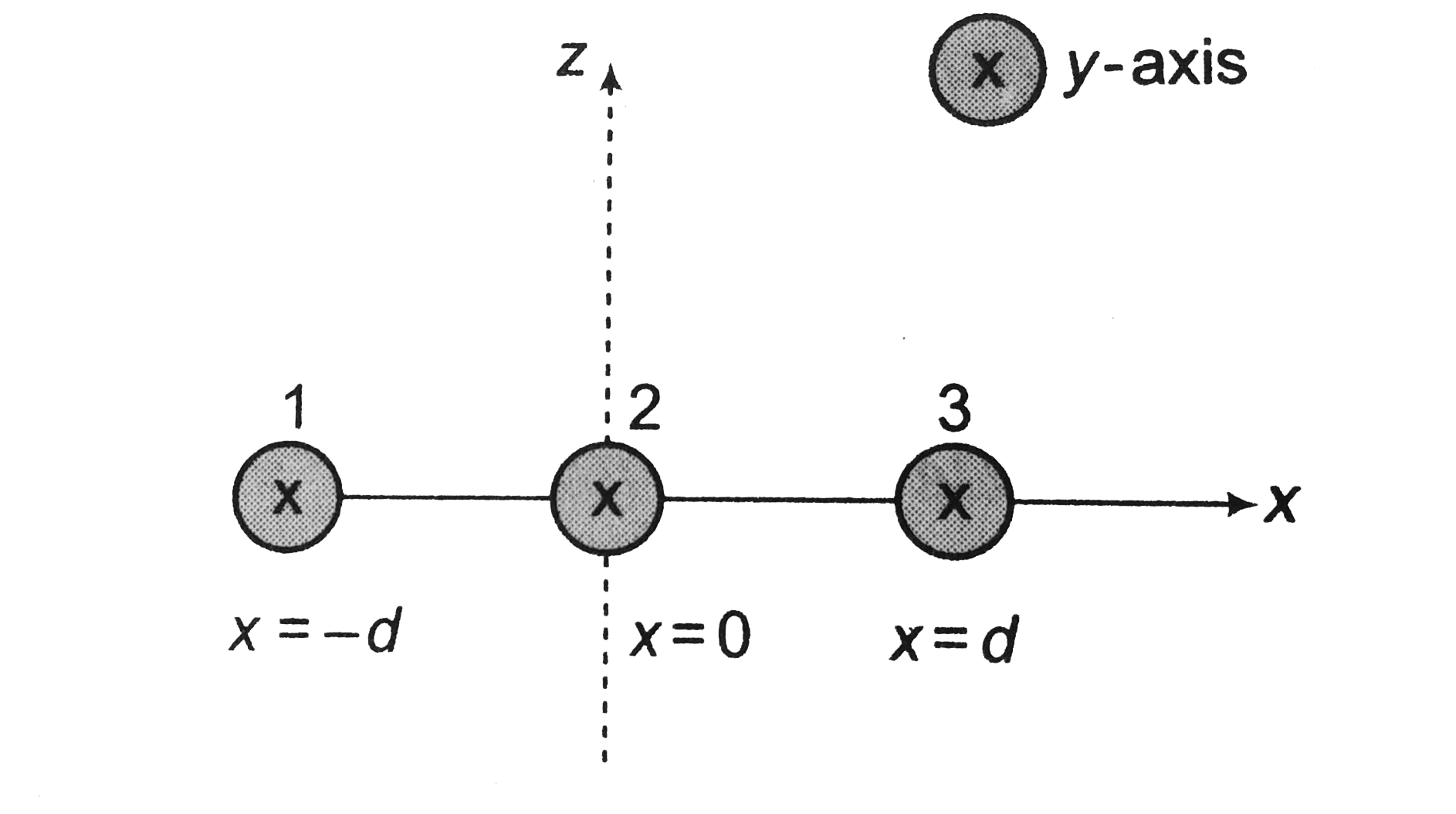
Three infinitely long thein wires, each carrying curren i int eh same diecrtion, are the dxy plane of a gravilty free space. The central wire is along the y-axis while the other two are along x=±d
i find the locus of the points for which the magnetic field B is zero.
ii If the central wire is displaced along the z-direction by a smal amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is λ, find the frequency of oscillation.
i. Magnetic field will be zero on the y-axis i.e.x=0=z

Magnetic field cannot be zero in region I and egion IV because in reion I magnetic field will be along positive z-direction due to all the three wires, while in region IV magnetic field will be along negative z-axis due to all the three wires. It can be zero only i reginn II and III.
Let magnetic field is zero on line z=0 and x=x (shown as dotted). The magnetic field on the line due to wire 1 and 2 will be along negative z-axis and due to wire 3 along positive z-axis. Thus,

B1+B2=B3
or μ02πi(d+x)+μ0i2πx=μ02πi(d−x)
or1d+x+1x=1d−x
this equation gives x=±d√3
Hence there will be two lilnes x=d√3
and x=−d√3(z=0)
where magnetic field is zero.
ii. In this part we chasnge our coordinate axes sytem, just for better understanding.
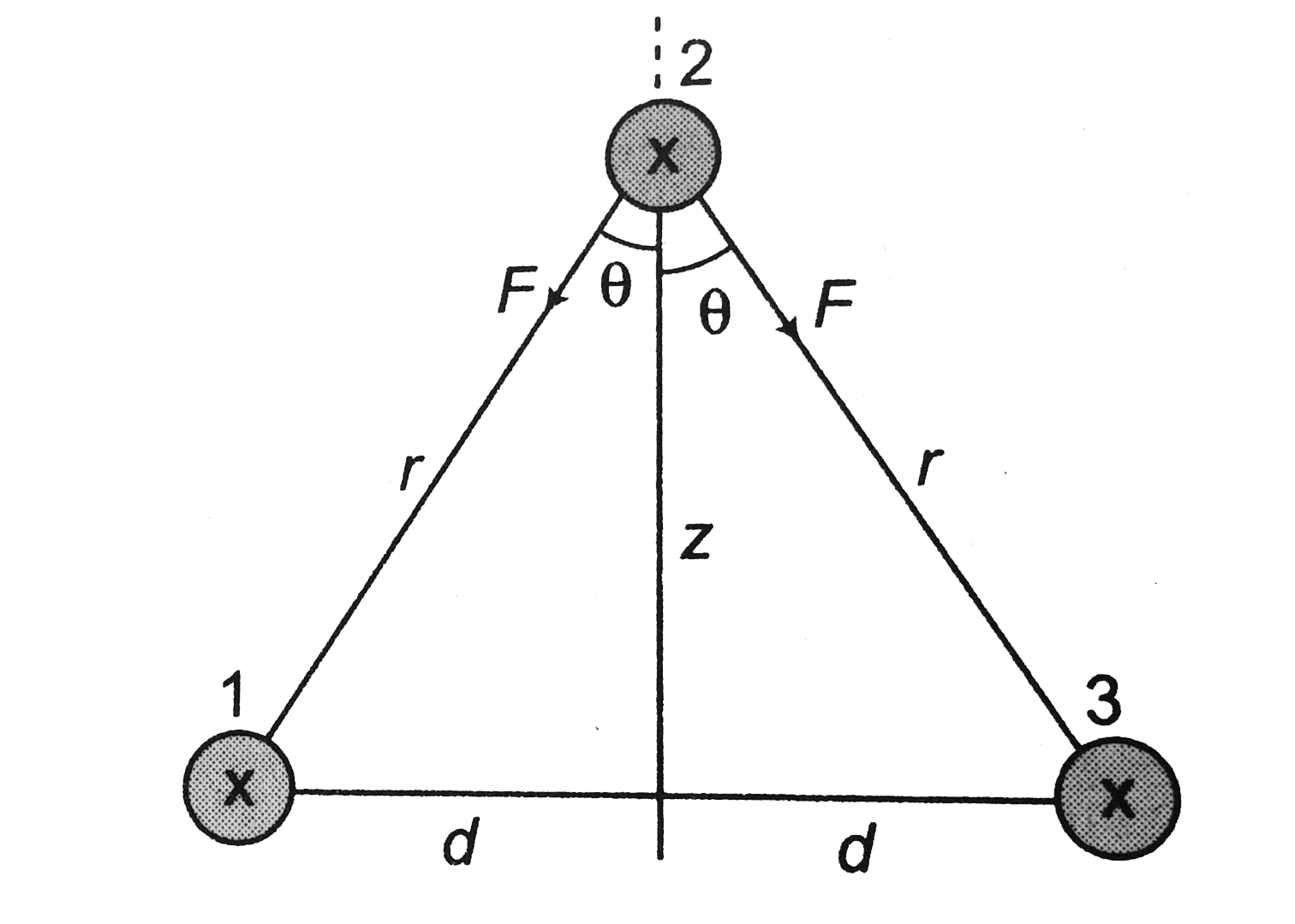
There are three wires 1,2, and 3 as shown in figure. Ilf we displace the wire 2 towards the z-axis, then force of attraction per unit length between wire (1 and 2) and (2 and 3) will be given by
f=μ02πi2r
The componetns of F along x-axis will be canceled out. Net resultant force will be towards negative z-axis (or mean position) and will be given by
Fnet=2Fcosθ=2{μ02πi2r}zr
Fnet=μ0πi2(z2+d2).z(r2=z2+d2)
If z<<d then
z2d2=d2
and Fnet=(μ0πi2d2).z
Negative sign implies that Fnet is restoring in nature.
∴,Fnet∝−z
i.e. the wire will oscillate simple harmonically,
let a be the acceleration of wire in this position and λ the mass per unit length of wire, then
Fnet=λa−(μ0πi2d2)z
orap=(m0i2πλd2)z
∴Frequency of oscillation
f=12π√∣accelerationdisplacement∣
12π√∣∣az∣∣=12πid√m0πλ
or f=12πd√μ0πλ)
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - Exercise
160 Videos
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
Three infinitely long thin wires, each carrying current i in the same direction, are in the x−y plane of a gravity free space . The central wire is along the y−aξs while the other two are along x=±d.
(i) Find the locus of the points for which the magnetic field B is zero.
(ii) If the central wire is displaced along the Z−direction by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is λ, find the frequency of oscillation.
View SolutionThree infinitely long thin wires each carrying current I in the same direction are in x−y plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d. If the central wire is slightly displaced along z-axis and released, show that it will execute S.H.M. The linear mass density of the wire is λ. If the time period of this small oscillation is kπdI√πλμ0, then find the value of k.
View Solution
Knowledge Check
Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is
 Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πrTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
ASquare of the magnetic field produced due to each of the wiresBhalf of the magnetic field produced due to each of the wiresCtwice the magnetic field produced due to each of the wiresDzeroTwo infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wiresBHalf of the magnetic field produced due to each of the wiresCSquare of the magnetic field produced due to each of the wiresDZero
Three infinitely long wires,each carrying equal current are placed in the xy -plane along x= 0,+d and−d.On the xy -plane,the magnetic field vanishes at
View SolutionThree long wires, each carrying current i are placed as shown. The middle wire is along Y-axis. The locus of point on the X-axis where magnetic field is zero is
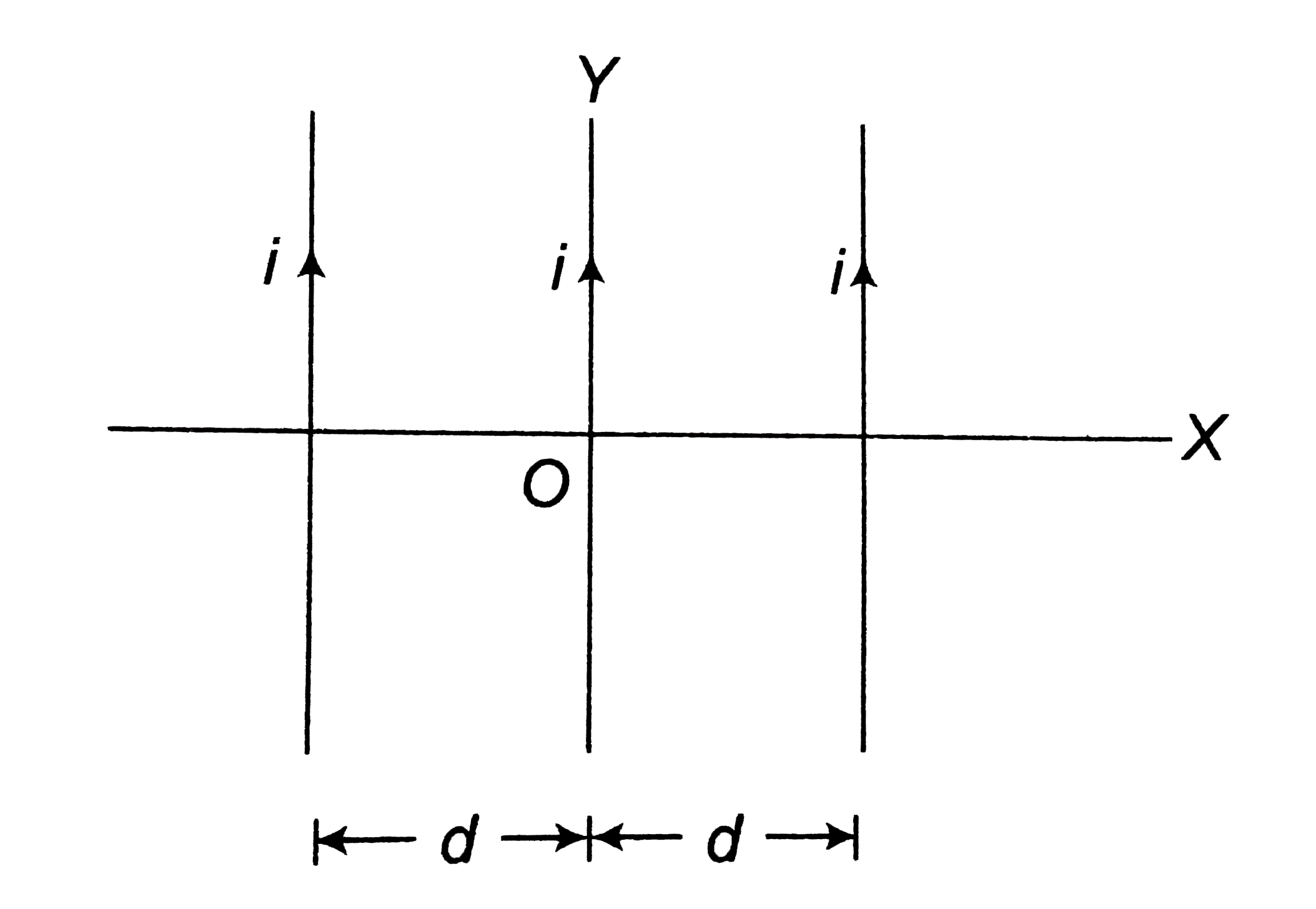
View SolutionTwo long wire carrying current 2i and i are placed along co-ordinate axes x and y respectively. The locus of point where magnetic field is zero is
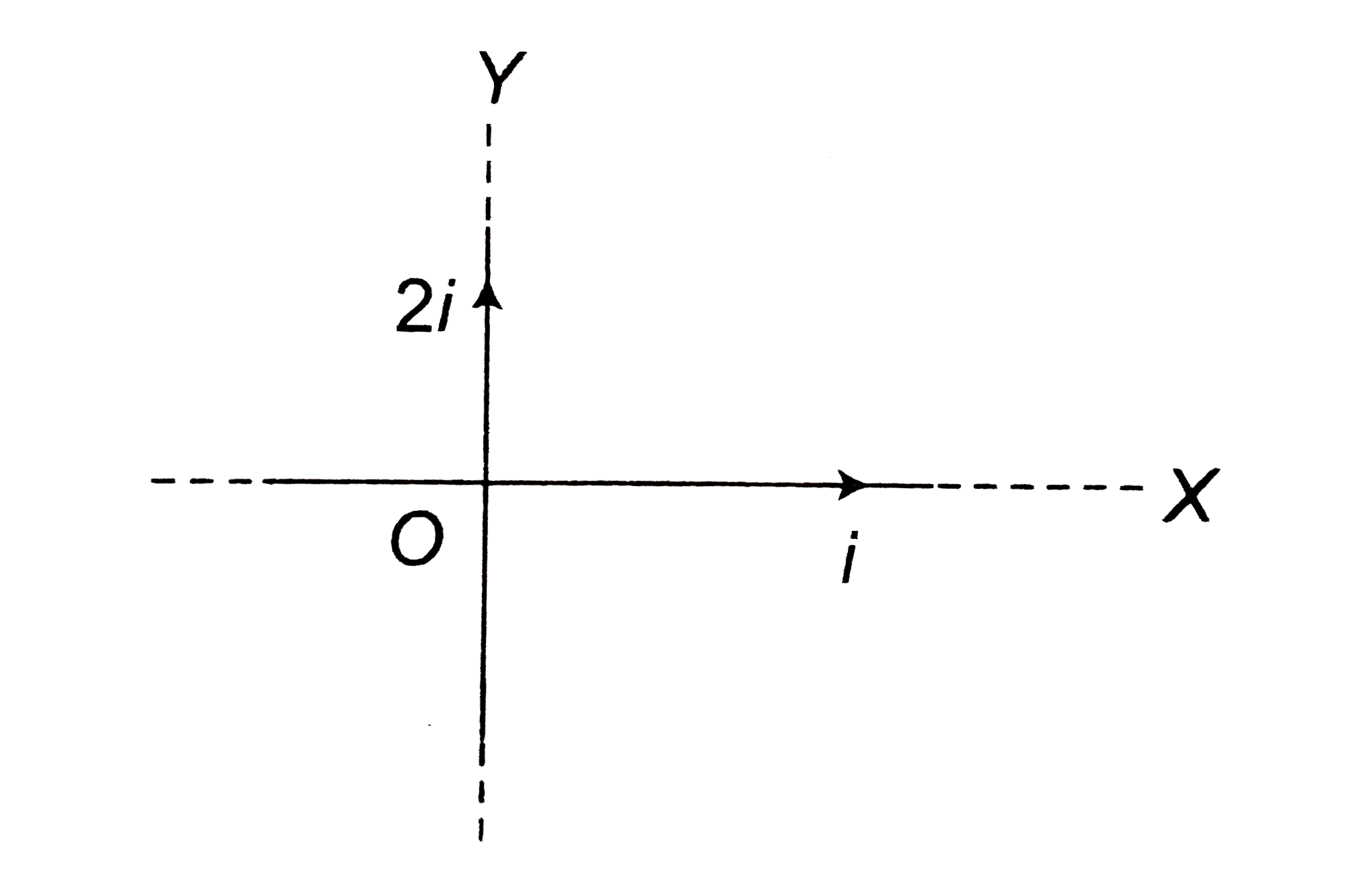
View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
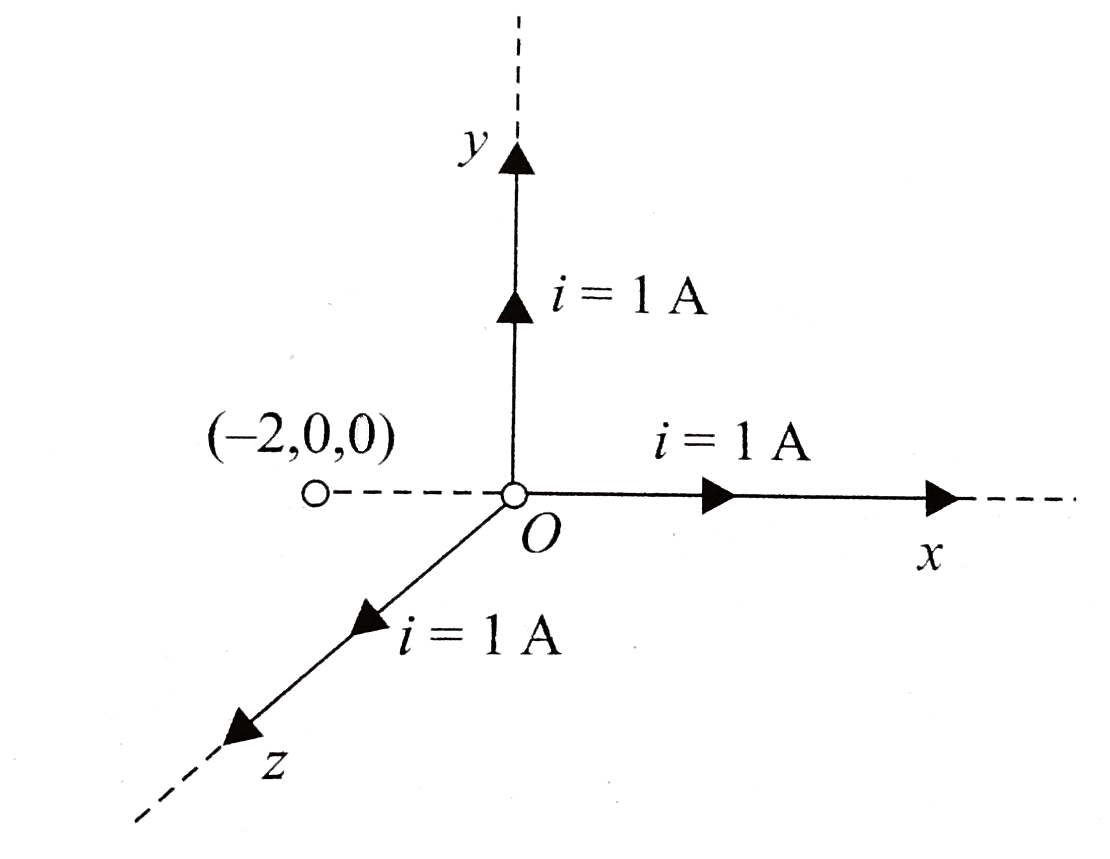
View Solutiontwo infinite wires, carrying currents i1andi2., are lying along x-and y-axes, as shown in the x-y plane. Then,
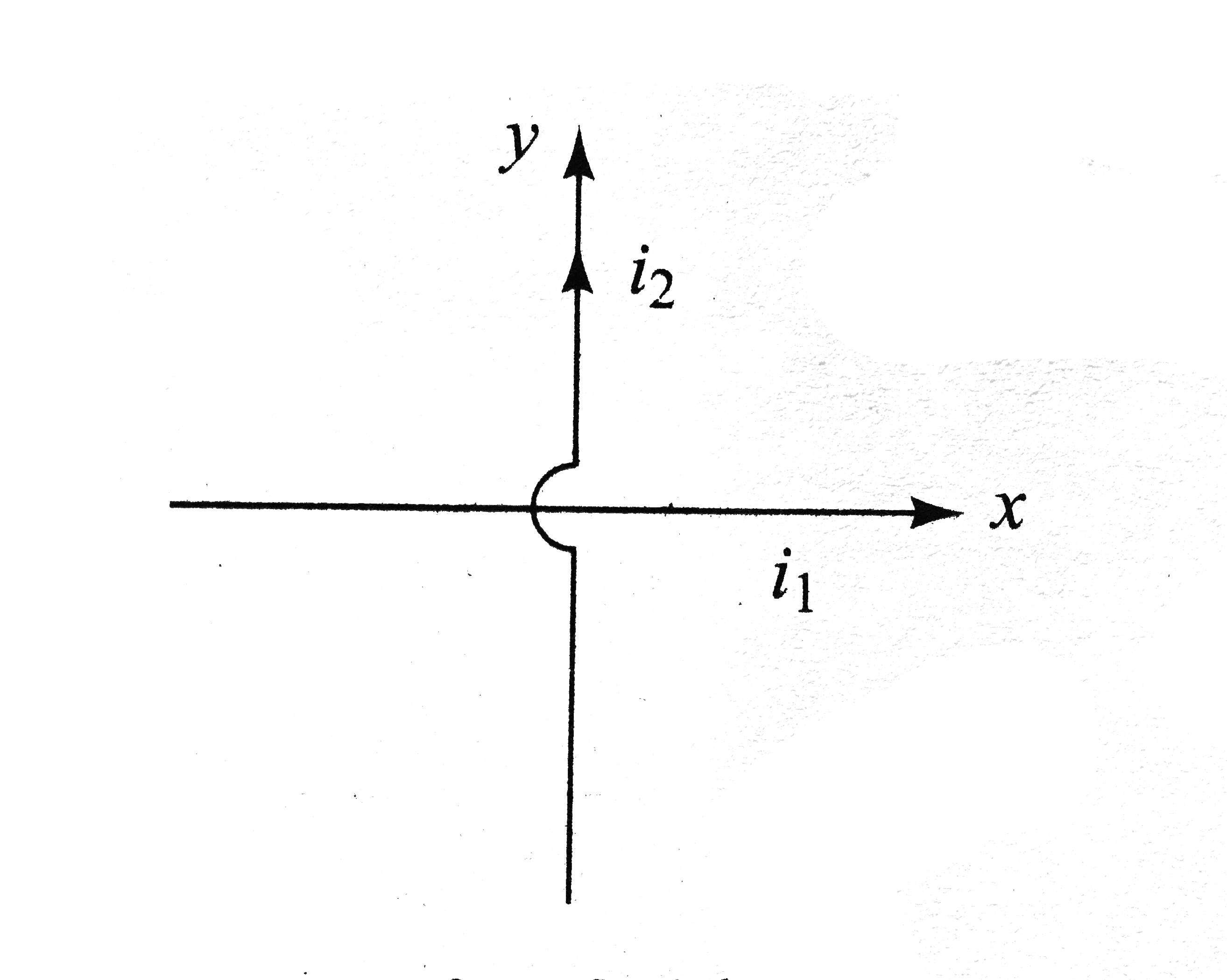
View Solution
