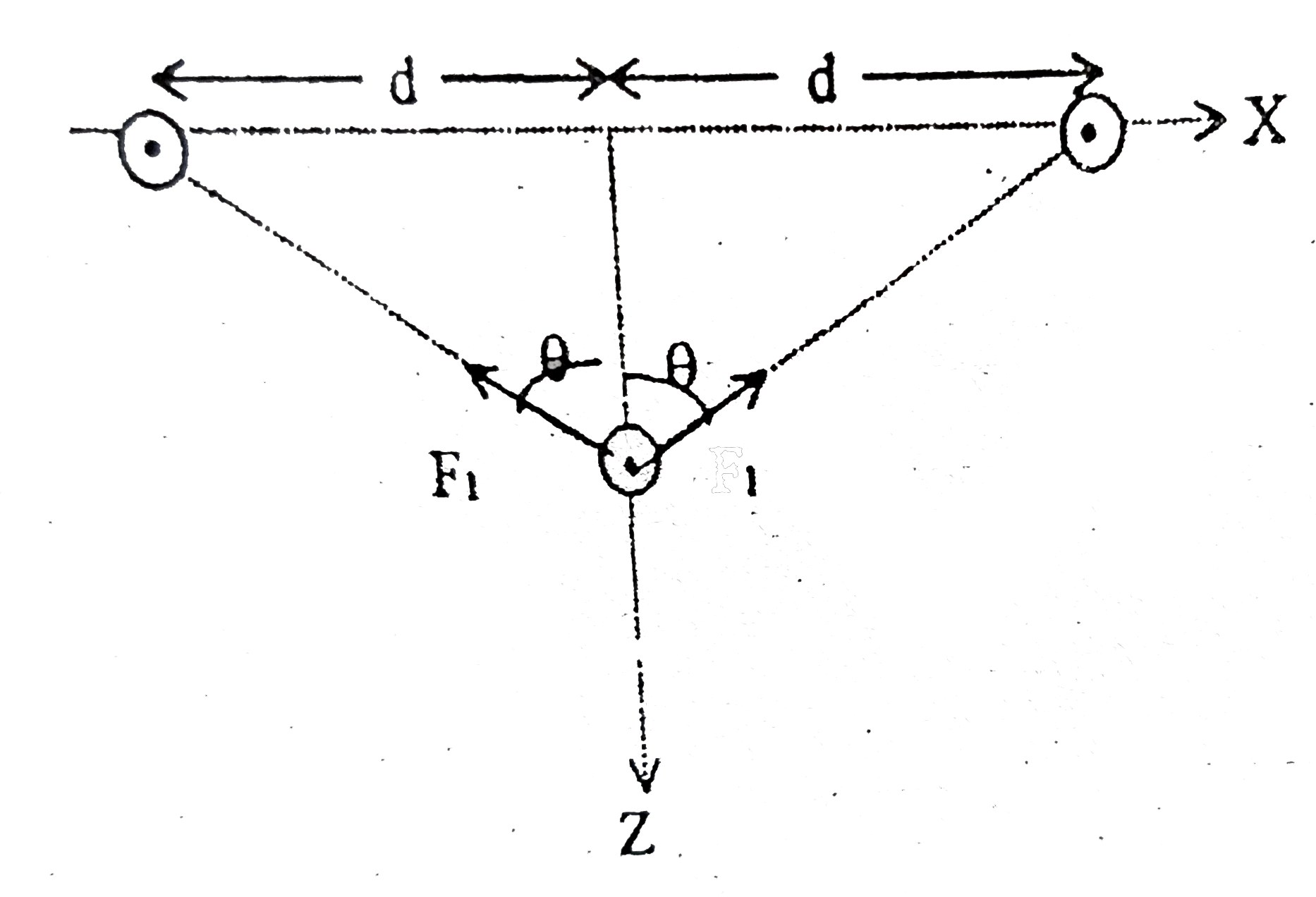
Three infinitely long thin wires each carrying current I in the same direction are in x−y plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d. If the central wire is slightly displaced along z-axis and released, show that it will execute S.H.M. The linear mass density of the wire is λ. If the time period of this small oscillation is kπdI√πλμ0, then find the value of k.
Let the central wire is displaced along z-axis by a small distance z and released.
Net restoring force on the central wire
F=−2F1cosθ (F1= is the magnitude of force on central wire due to either of the other two wires)
=−2μ0I22πrzrl
=−μ0I2zπ(d2+z2)l
=−μ0I2zπd2l (Since z<<d⇒z2+d2≈d2)
Acceleration of the central wire
a=Fλl=−μ0I2πλd2z
comparing this equation with equation of SHM
a=−ω2x
⇒ω=√μ0πλId
⇒T=2πω=2πdI√πλμ0
Topper's Solved these Questions
Similar Questions
Three infinitely long thein wires, each carrying curren i int eh same diecrtion, are the dxy plane of a gravilty free space. The central wire is along the y-axis while the other two are along x=±d
i find the locus of the points for which the magnetic field B is zero.
ii If the central wire is displaced along the z-direction by a smal amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is λ, find the frequency of oscillation.
View SolutionThree infinitely long thin wires, each carrying current i in the same direction, are in the x−y plane of a gravity free space . The central wire is along the y−aξs while the other two are along x=±d.
(i) Find the locus of the points for which the magnetic field B is zero.
(ii) If the central wire is displaced along the Z−direction by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is λ, find the frequency of oscillation.
View Solution
Knowledge Check
Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is
 Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πrA long straight wire is carrying current I in + z direction .The x-y plane contains a closed circular loop carrying current I2 and not encircling the straight wire.The force on the loop will be
Aμ0l1l0/2πBμ0l1l0/4πCzeroDdepends on the distacne of the centre of the loop from the wireThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
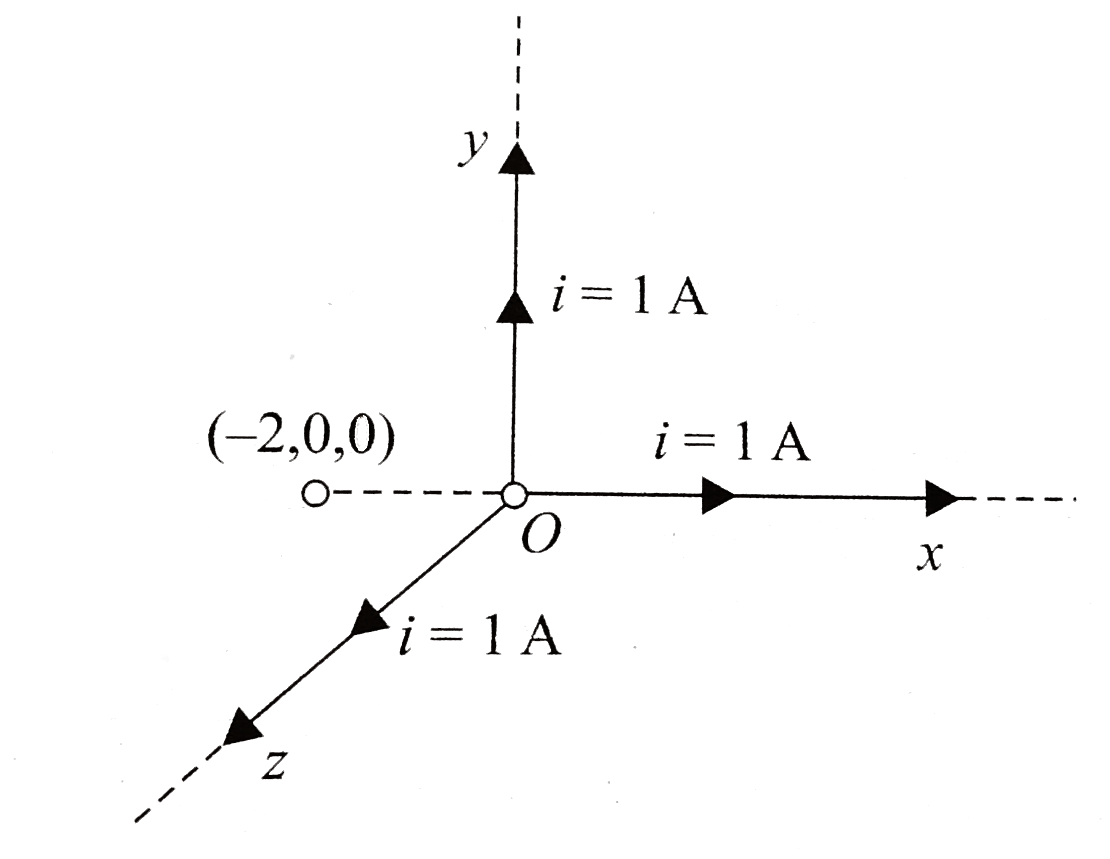 Aμ04π(ˆj+ˆk)Bμ04π(ˆj−ˆk)Cμ08π(−ˆj+ˆk)Dμ08π(ˆj+ˆk)
Aμ04π(ˆj+ˆk)Bμ04π(ˆj−ˆk)Cμ08π(−ˆj+ˆk)Dμ08π(ˆj+ˆk)
Three infinitely long wires,each carrying equal current are placed in the xy -plane along x= 0,+d and−d.On the xy -plane,the magnetic field vanishes at
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionThere is a circular loop carrying current and another straight wire carrying current is placed along its axis. The straight wire
View SolutionA long straight wire is carrying current I1 in +z direction, The x-y plane contains a closed circular loop carrying I1 and not encircling the straight wire. The force on the loop will be
View SolutionThree long wires, each carrying current i are placed as shown. The middle wire is along Y-axis. The locus of point on the X-axis where magnetic field is zero is
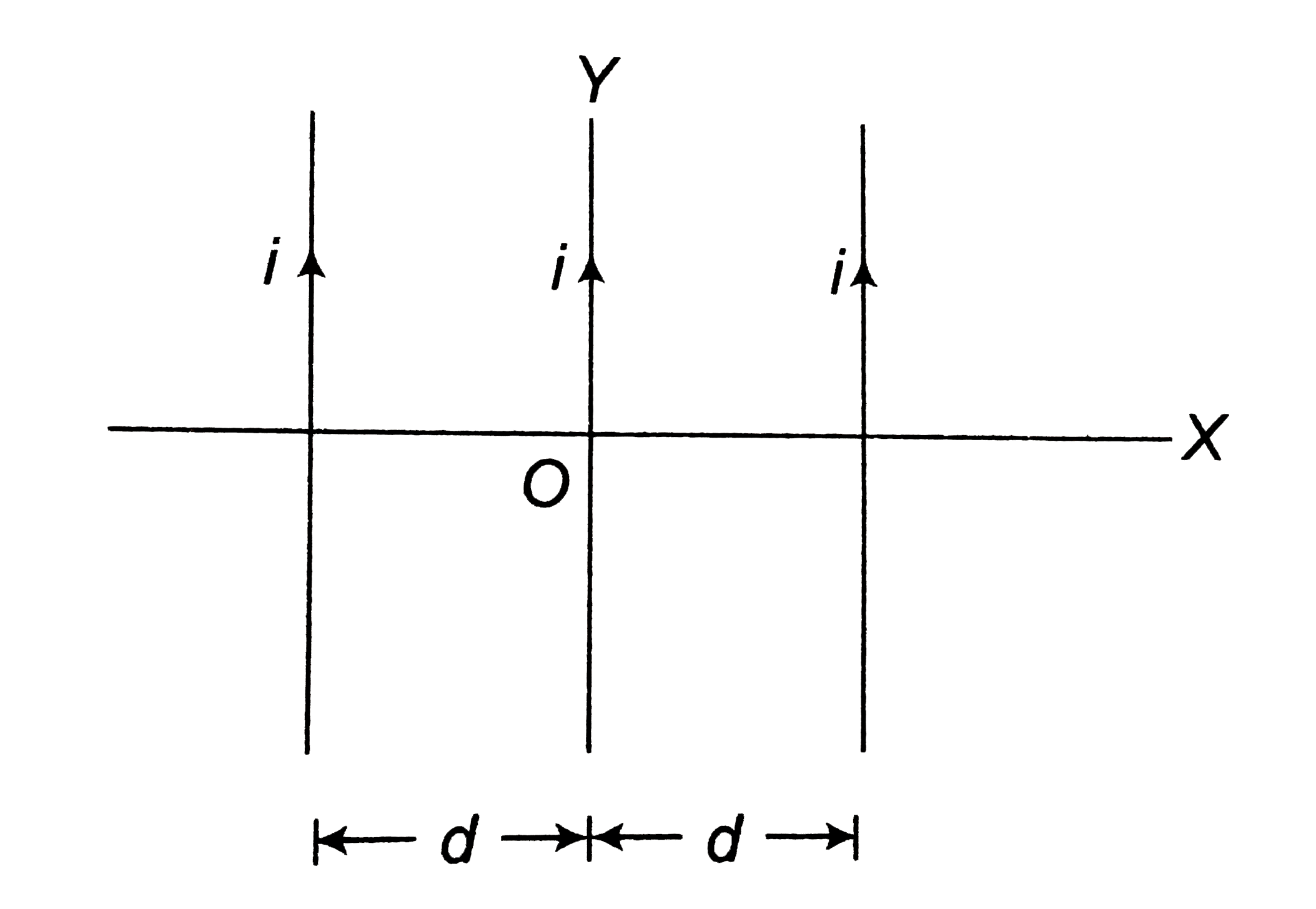
View Solution

