A thin wire is wound very tightly in one layer on the surface of a sphere of paramagnetic material (μr≈1). The planes of all the turns can be assumed to be perpendicular to the same diameter of the sphere. The turns over the entire surface of the sphere. The radius of the sphere is R, the total number of turns is N, and the current in the winding is I. Find the magnetic induction at the centre of the sphere. (Given μ0NI=20R)
Video Solution
Text Solution
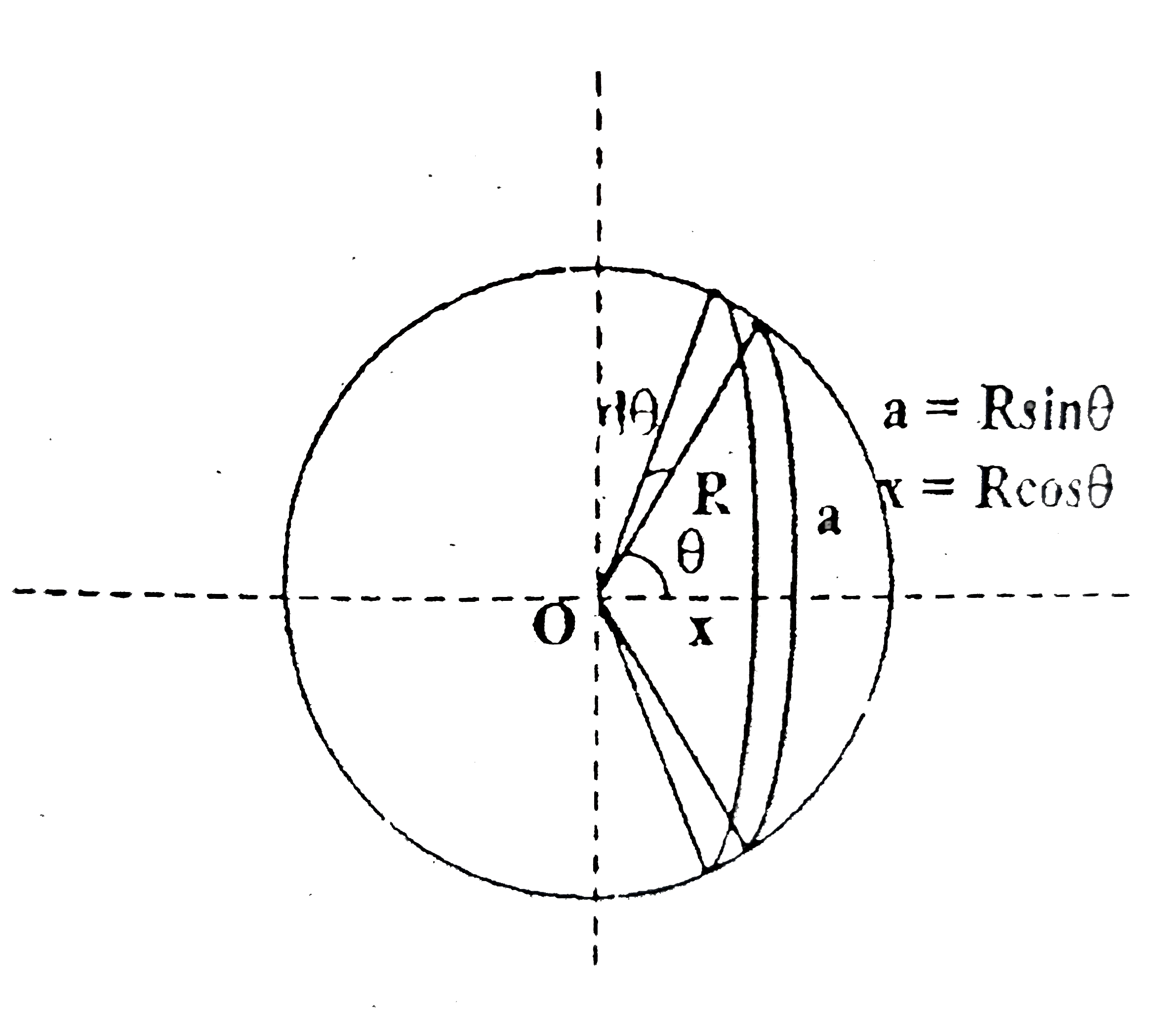
Consider a circular ring of radius 'a' at a distance x from the centre O such that
a=Rsinθ
x=Rcosθ
The number of turns dN in the length Rdθ is
dN=NπR(Rdθ)=Nπdθ
Magnetic induction at the centre of the sphere due to the ring is dB=μ0NπdθIx22(a2+x2)3/2dx=μ02πNIRsin2θdθ
On integrating
B=μ0NI2πR∫π0sin2θdθ
B=μ0NI2πR[π2] or B=μ0NI4R
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The radius of a sphere is 21cm, what is the surface area of the sphere?
A12932cm2B4312cm2C9702cm2D5544cm2Flux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
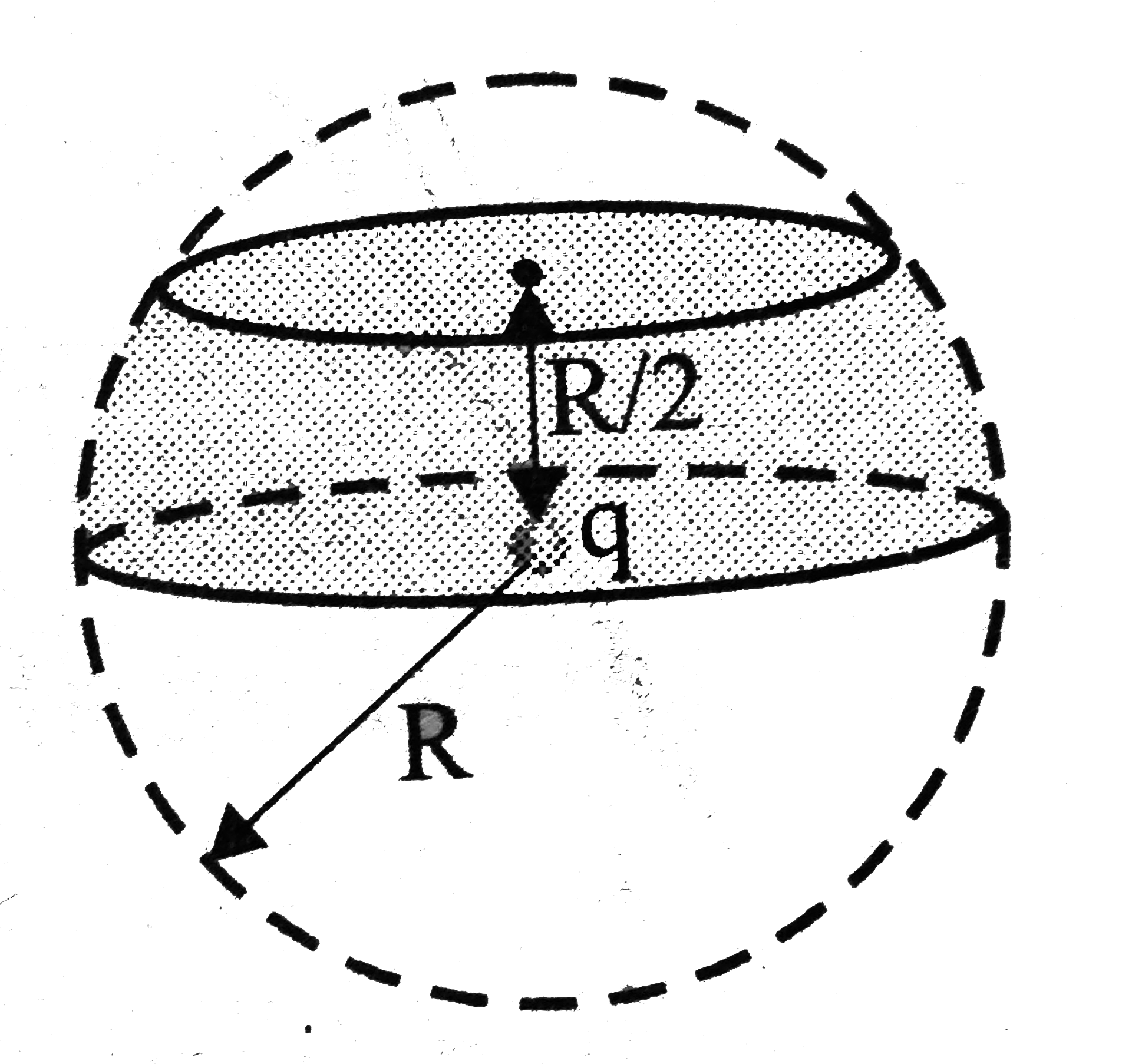 Aqε0Bq2ε0Cq4ε0Dzero
Aqε0Bq2ε0Cq4ε0DzeroIf the volume of a sphere is numerrically equal to its surface area. Then radius of sphere is
A1 unitB3 unitC2 unitD6 unit
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionIf the surface area of sphere is 256πcm2. Then find the diameter of the sphere.
View SolutionRadius of a sphere is 14 cm. Find the surface area of the sphere.
View SolutionFor a sphere made out of a certain material, the moment of inertia of the sphere is proportional to [ radius of the sphere = R ]
View SolutionThe magnitude of surface area of sphere is half the magnitude of the volume of the sphere . Find the diameter of the sphere .
View Solution

