There is a circular loop carrying current and another straight wire carrying current is placed along its axis. The straight wire
will apply radial inward force on the circular loop.
will apply radial outward force on the circular loop.
will apply force radially inward or outward, depending on the direction of currents.
will not exert any force on the circular loop.
The correct Answer is:D
To solve the problem of the interaction between a circular loop carrying current and a straight wire carrying current placed along its axis, we can follow these steps:
Step 1: Understand the Configuration
We have a circular loop with a current I1 flowing through it and a straight wire with current I2 placed along the axis of the loop. We need to analyze the magnetic field produced by the straight wire and its effect on the circular loop.
Hint: Visualize the setup clearly, noting the direction of currents in both the loop and the wire.
Step 2: Determine the Magnetic Field from the Straight Wire
A straight wire carrying current produces a magnetic field around it. The magnetic field B at a distance r from a long straight wire carrying current I2 is given by the formula:
B=μ0I22πr
where μ0 is the permeability of free space.
Hint: Remember that the magnetic field lines form concentric circles around the wire.
Step 3: Analyze the Magnetic Field at the Loop
Since the straight wire is along the axis of the circular loop, the magnetic field at any point on the loop will be directed tangentially to the loop. The direction of the magnetic field can be determined using the right-hand rule.
Hint: Use the right-hand rule to determine the direction of the magnetic field produced by the straight wire.
Step 4: Calculate the Force on the Loop
The force dF on a small segment dL of the loop due to the magnetic field B is given by:
dF=I1dL×B
The angle between dL (tangential to the loop) and B (also tangential) is 180∘ (or π radians), which means:
sin(180∘)=0
Thus, the force dF becomes zero:
dF=I1dL⋅B⋅sin(180∘)=0
Hint: Remember that the cross product is zero when the vectors are parallel or anti-parallel.
Step 5: Conclude the Interaction
Since the force dF is zero for every segment of the loop, the total force F on the entire loop is also zero. Therefore, the straight wire does not exert any net force on the circular loop.
Hint: Consider the implications of having zero force at every point on the loop.
Final Answer
The straight wire will not exert any force on the circular loop.
Correct Option: The straight wire will not exert any force on the circular loop.
We have a circular loop with a current I1 flowing through it and a straight wire with current I2 placed along the axis of the loop. We need to analyze the magnetic field produced by the straight wire and its effect on the circular loop.
A straight wire carrying current produces a magnetic field around it. The magnetic field B at a distance r from a long straight wire carrying current I2 is given by the formula:
B=μ0I22πr
where μ0 is the permeability of free space.
Since the straight wire is along the axis of the circular loop, the magnetic field at any point on the loop will be directed tangentially to the loop. The direction of the magnetic field can be determined using the right-hand rule.
The force dF on a small segment dL of the loop due to the magnetic field B is given by:
dF=I1dL×B
The angle between dL (tangential to the loop) and B (also tangential) is 180∘ (or π radians), which means:
sin(180∘)=0
Thus, the force dF becomes zero:
dF=I1dL⋅B⋅sin(180∘)=0
Since the force dF is zero for every segment of the loop, the total force F on the entire loop is also zero. Therefore, the straight wire does not exert any net force on the circular loop.
The straight wire will not exert any force on the circular loop.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
79 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
28 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )
18 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A circular loop of radius r carries a current i. How should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
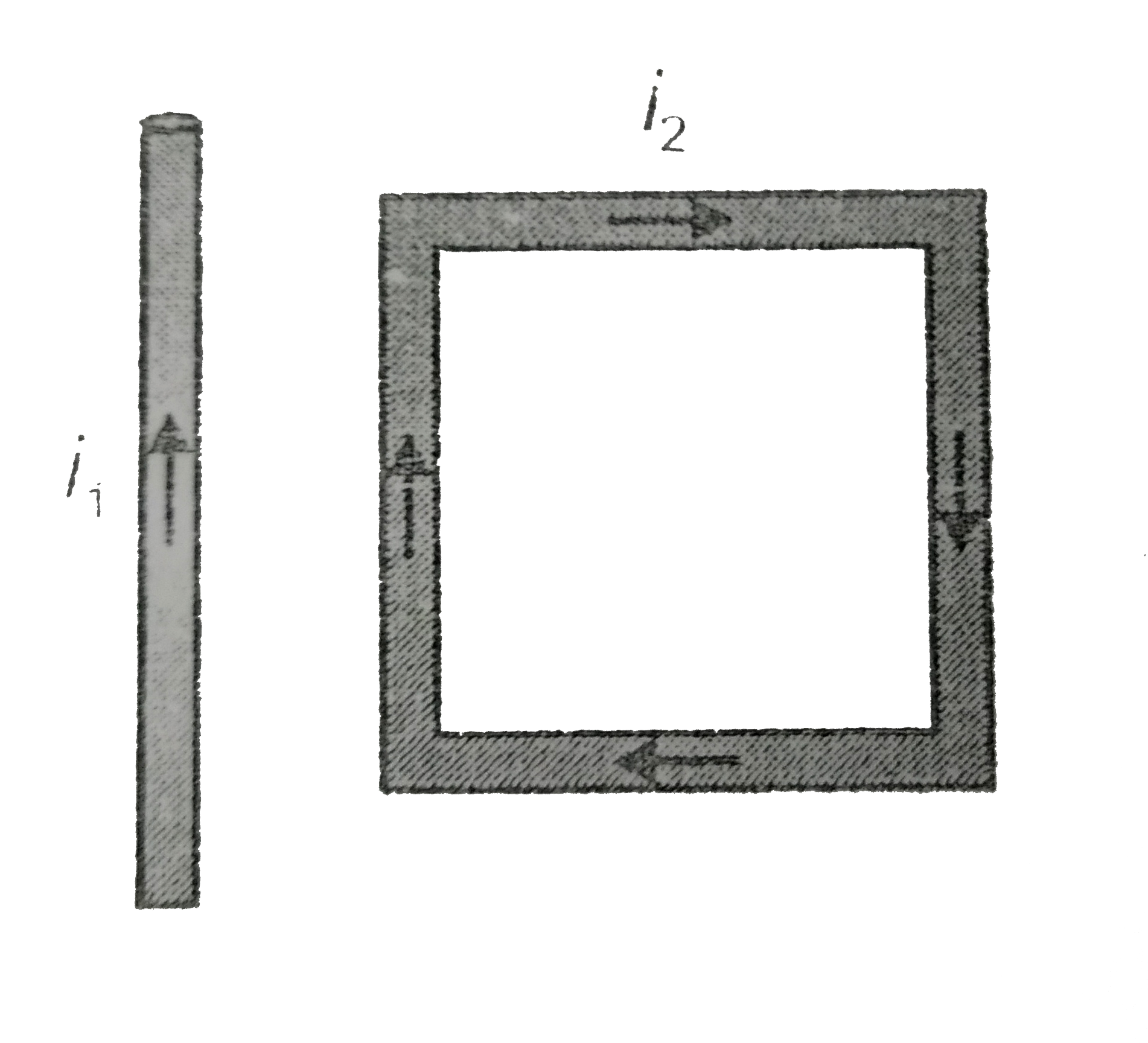
View Solution
Knowledge Check
A straight wire carrying current is parallel to the y-axis as shown in Fig. The
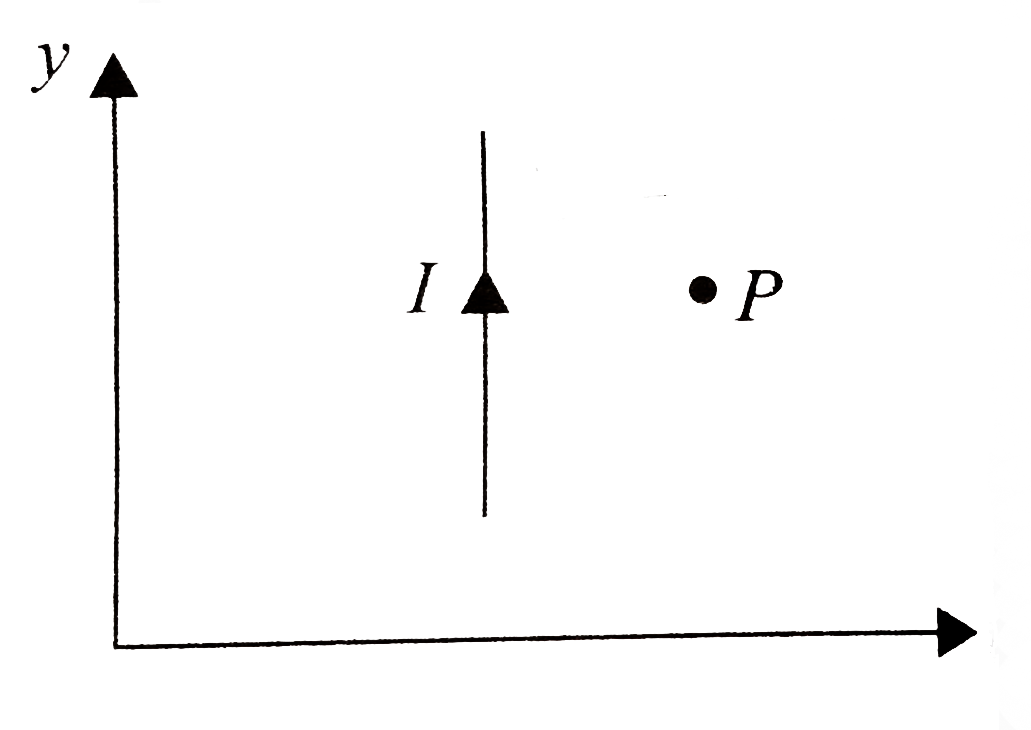 Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.
Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.A straight wire is carrying an electric current
Athere are no magnetic lines of force near the wireBthere are lines of force and they are circular lines encircling the wireCthe lines of force are straight lines parallel to the wire and in the direction opposite to the currentDthe lines of force are straight lines parallel to the wire in the direction opposite to the current.A field due to a long straight wire carrying a current I is proportional to
AlBl2Cl3D√l
A circular loop of radius r carries a current i.How should a long, straight wire carrying a current 3i be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
View SolutionThe magnetic field lines due to a straight wire carrying a current are
View Solution
