A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

μ0I2πR(π+1)
μ0I4πR(π2+1)
μ0I4πR(π−1)
μ0I4πR(π+1)
The correct Answer is:D
The portion of the wire through DE if extended backwards passes through the point O and hence it will not produce any magnetic field at point O. AB is semi-infinite wire for the point o and there is one half circle after point B, both are producing magnetic field inwards per the direction of the current, hence to calculate the net magnetic field, both of these fields will be added. Net magnetic field at the point O can be written as:
B=μ0I4R+μ0I4πR=μ0I4πR(π+1)
Hence, option (d) is correct.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
79 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
28 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )
18 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
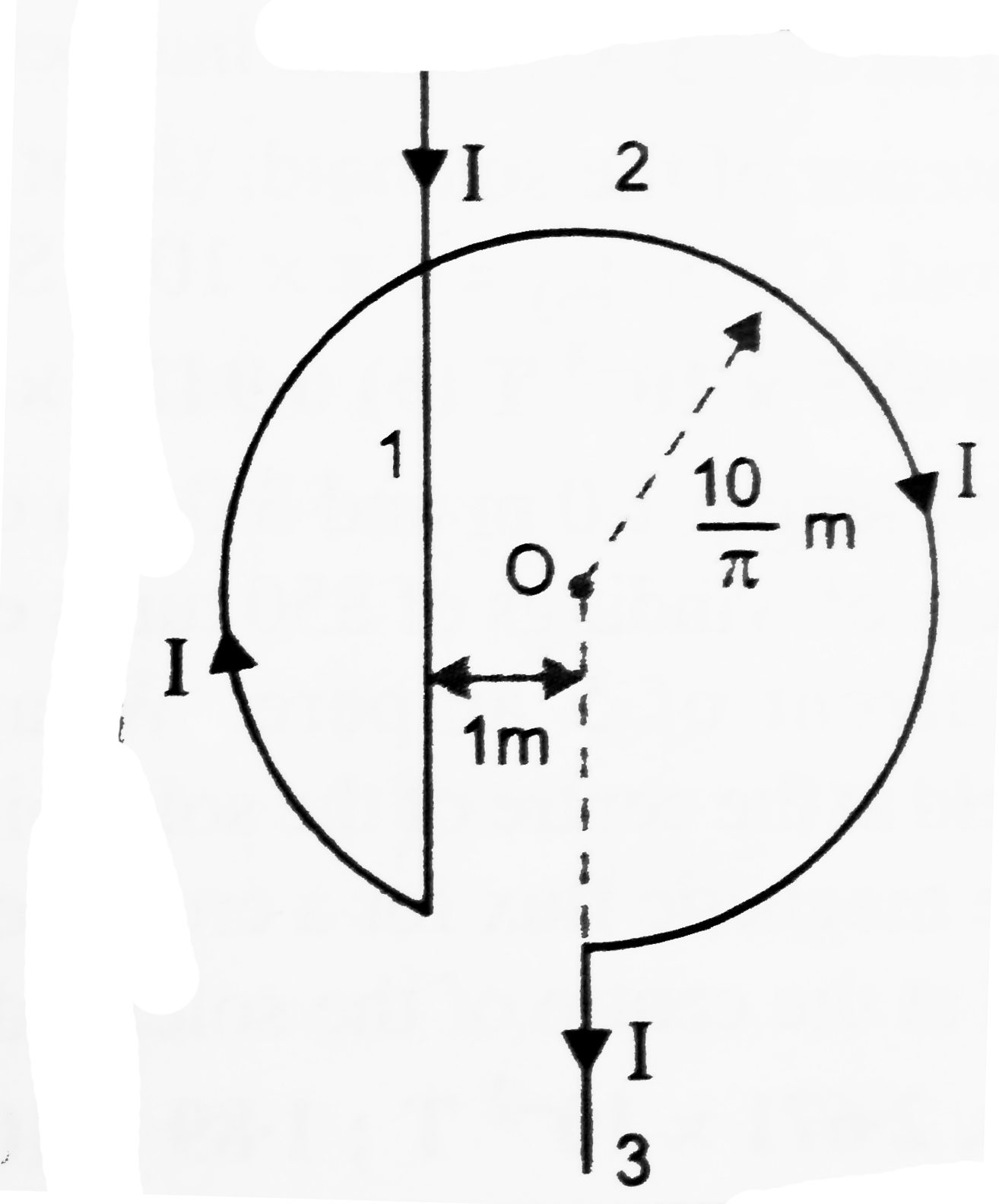
View SolutionTwo inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
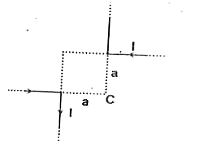
View Solution
Knowledge Check
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)Four infinitely long 'L' shaped wires, each carrying a current I have been arranged as shown in the figure. Obtain the magnetic field intensity at the point 'O' equidistant from all the four corners.
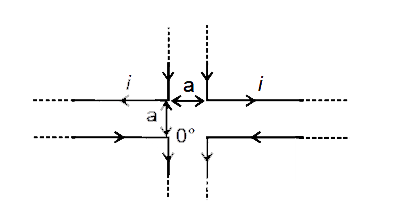 A1wb/m2B0wb/m2C2wb/m2Dnone of these
A1wb/m2B0wb/m2C2wb/m2Dnone of these
" A long wire is bent into the hair pin-like shape shown in the figure.The magnetic induction at the point "P" is given by "
View Solutionone of the two infinitely long wires carrying current I is bent as shown in the adjacent figure. The magnetic induction at C is equal to
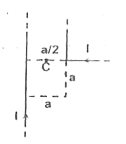
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
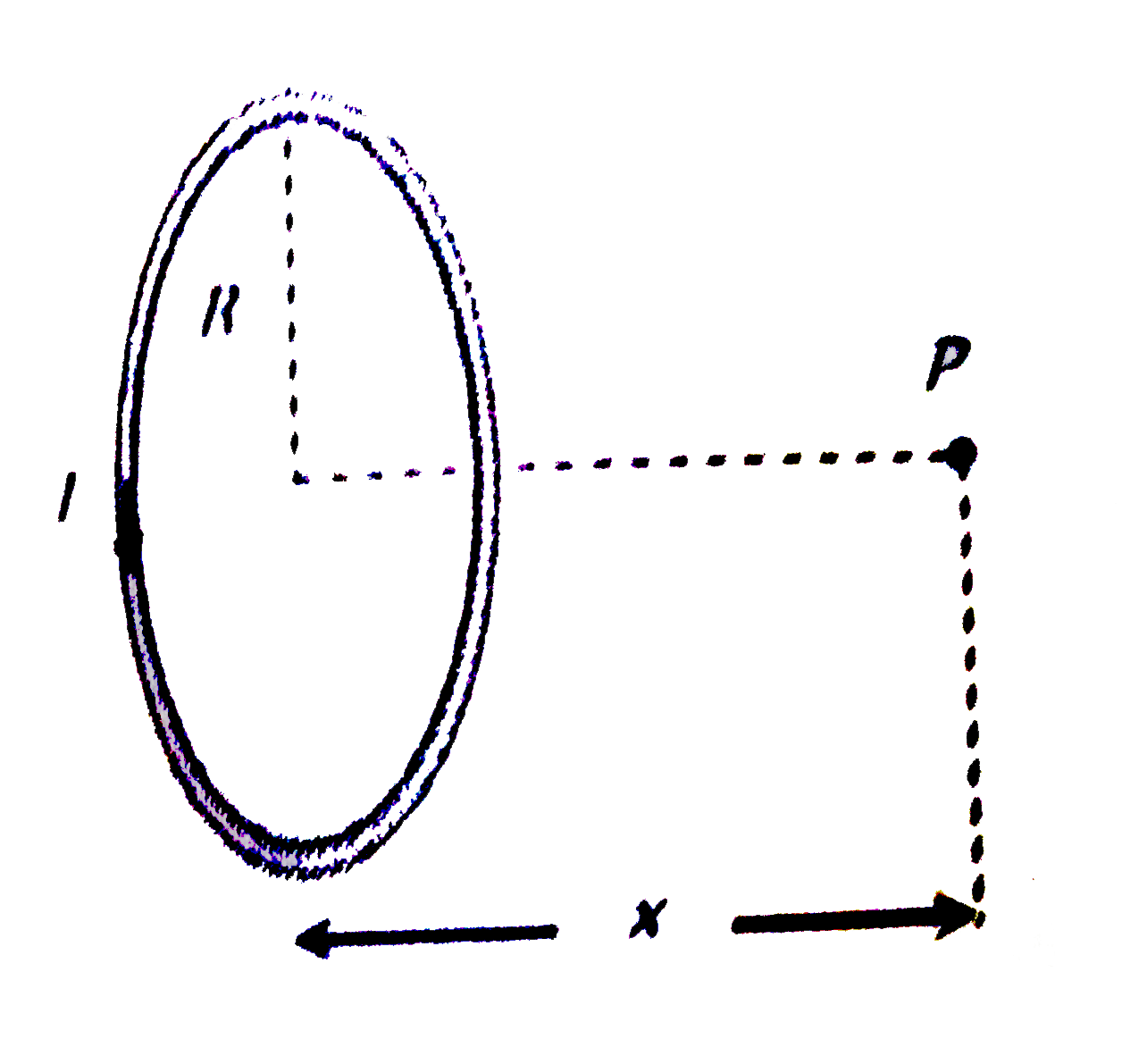
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View Solution
