A long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
Current density j=iπ(R∘−r2)
Current through the smaller cross section
i'=jπr2 (in absence of cavity)
Magnetic field due to this current at a point on the axis of bigger
cylinder
B1=μ0i'2πd=μ02πd×jπr2=(μ0)×iπ(R∘−r2)
Let B2 be the magnetic field due to remaining portion. Then
B1+B2=0orB2==−B1 or |B2|=|B1|
∴B2=μ0i2πd×r2R2−r2
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
View SolutionA current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius R1 and outer radius R2. Magnetic field B varies with distance r form the axis of the cylinder is
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

View SolutionA long thin walled pipe of radius R carries a current I along its length The current density is uniform over the circumference of the pipe The magnetic field at the center of the pipe due to quarter portion of the pipe shown, is
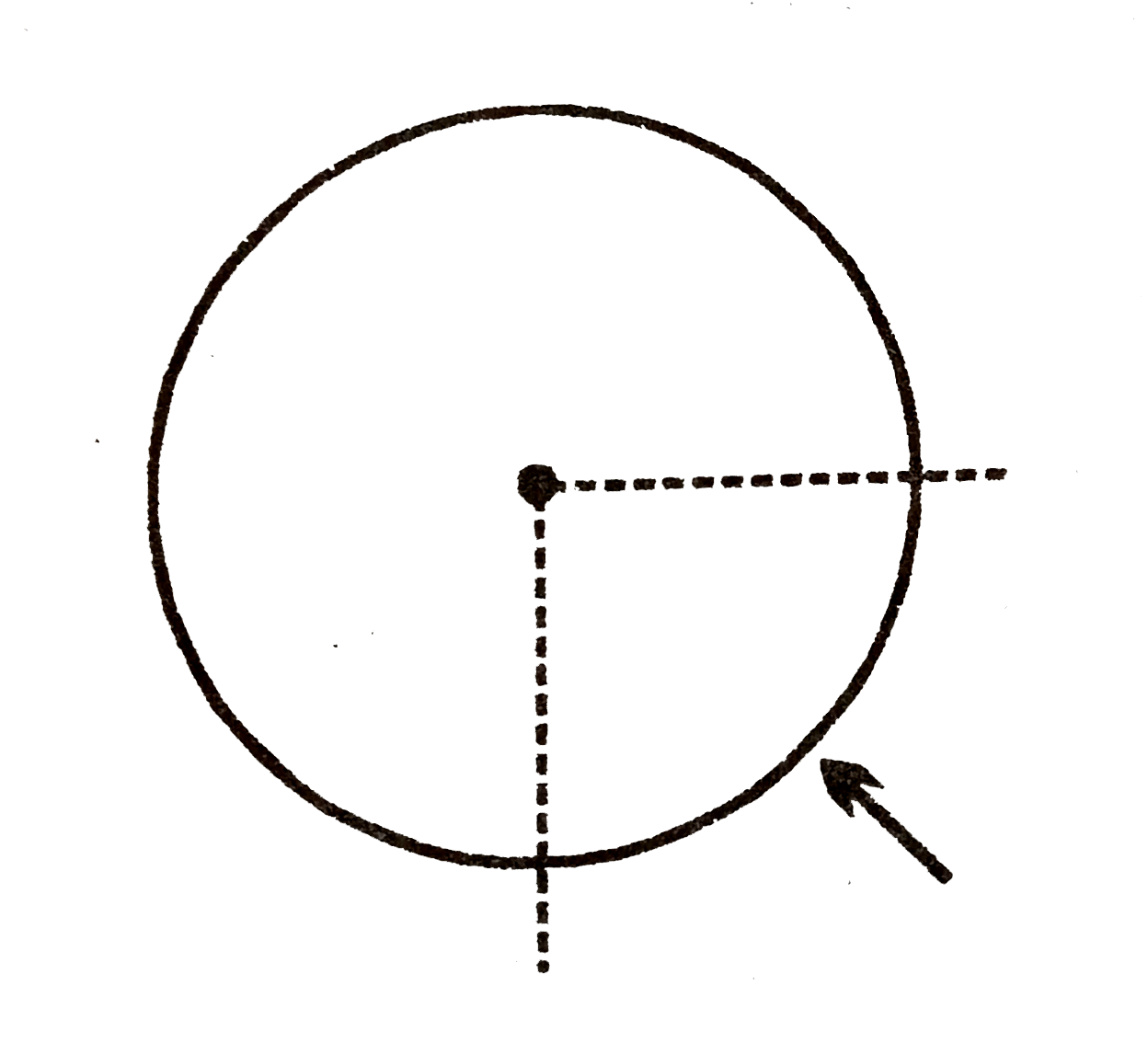 .
.
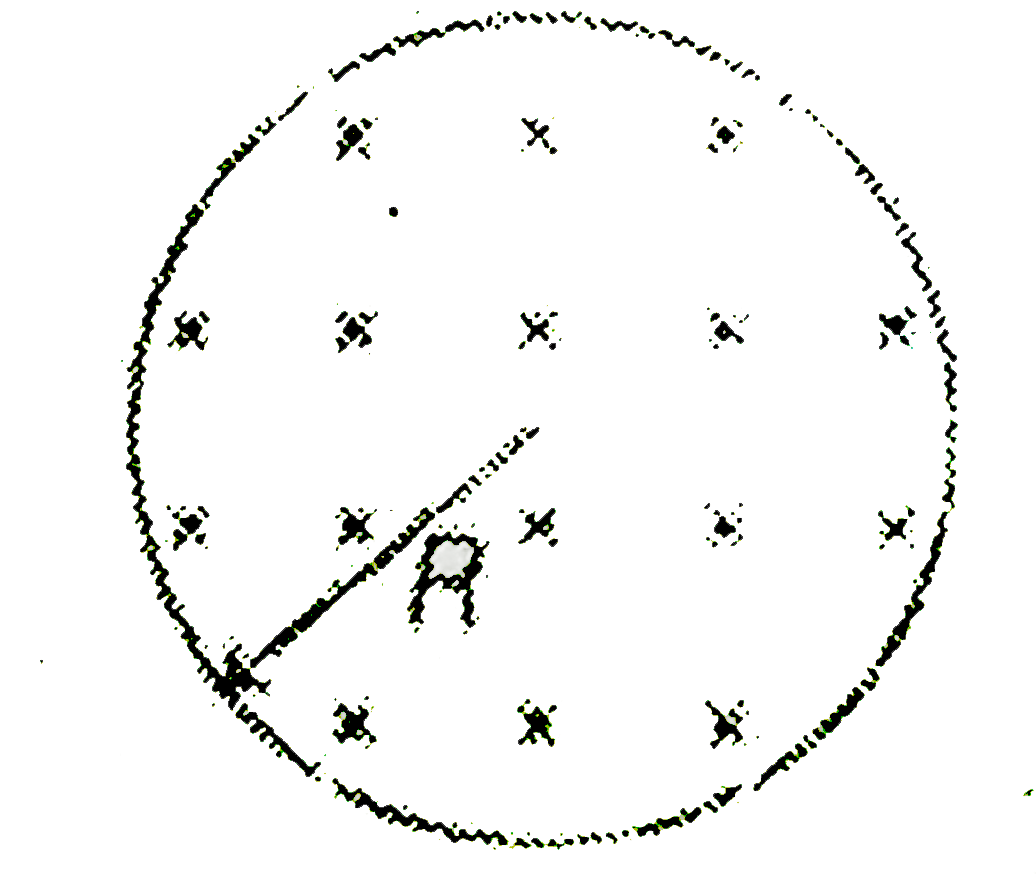
View SolutionA cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
View SolutionA rectangular sheet of paper 44cmAND18cm is a rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionA long cylinder of wire of radius 'a' carries a current i distributed uniformly over its cross section. If the magnetic fields at distances r<aandR>a from the axis have equal magnitude, then
View Solution
