A wire loop carrying a current I is placed in the xy-plane as shown in figure
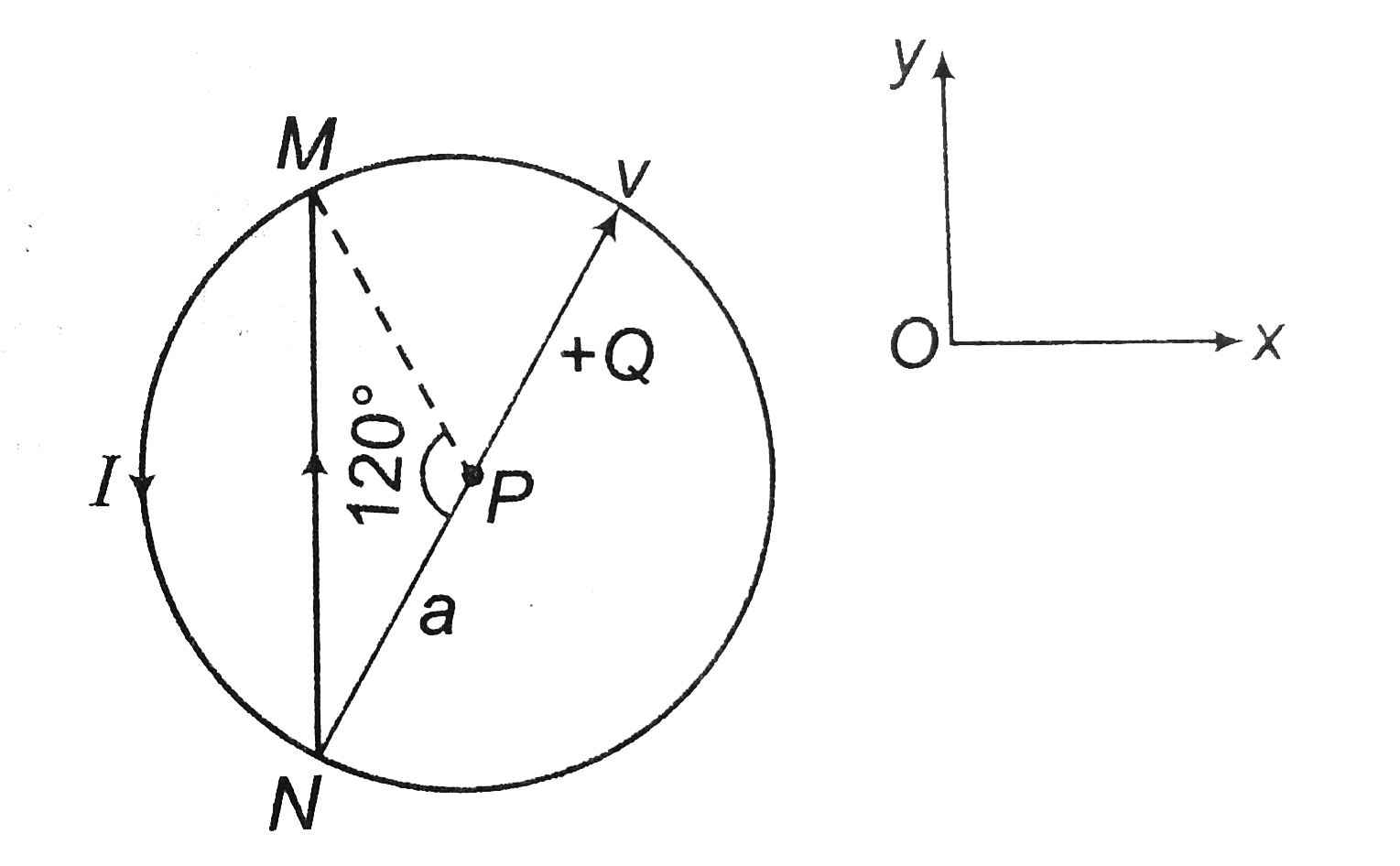
a. If a particle chsarge +Q and mass m is placed at in centre P and given a velocity v along NP (see figure), find its instaneous acceleration.
If an external uniform magnetic induction field B=Bˆi is applied, find the force and the torque acting on the loop due to this field.
(a) As in case of current-carrying straight conductor and arc,
the magnitude of B is given by
B1μ0I4πd(sinα+sinβ) and B2=μ0Iϕ4πr
So in accordance with right hand screw rule,
(→Bw)=μ4π1acos60∘×2sin60∘(−ˆk) and
(→B)MN=μ0I2a[2π/32π]ˆka
and hence net →B at P due to the given loop →B=→Bw+→BA⇒→B=μ04π2Ia[√3−π3](−ˆk)...(i)
Now as force on charged particle in magnetic field is
given by →F=q(→v×→B)
so here, vefF=qvBsin90∘ along PF
i.e. →F=μ04π2QvIa[√3−π3]alongPF
and so →a=→Fm=10−72QvIma[√3−π3]alongPF
(b) As d→F=Id→L×→B,so→F=∫Id→L×→B
As here I and →B are constant
→F=[∮d→L]×→B=0[as∮d→L=0]
Further as area of coil,
→S=[13πa2−12.2asin60∘×acos60∘]ˆk=a2[π3−√34]ˆk
so →M=I→S=Ia2[π3−√34]ˆk
and hence →τ=→M×→B=Ia2B[π3−√34](ˆk׈i)
⇒→τ=Ia2B[π3−√34]ˆjNm

Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.1
Explore 35 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.2
Explore 10 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionA circular loop carrying a current I is placed in the xy-plane as shown in figure. A uniform magnetic fied B is oriented along the positive z-axis. The loop tends to
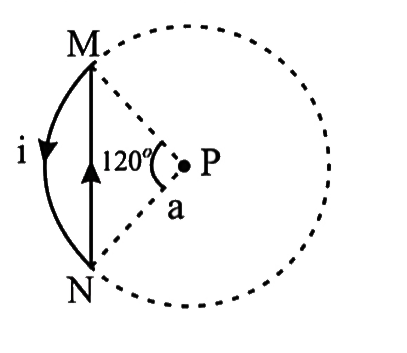
View SolutionA wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
View SolutionA circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30,A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure.
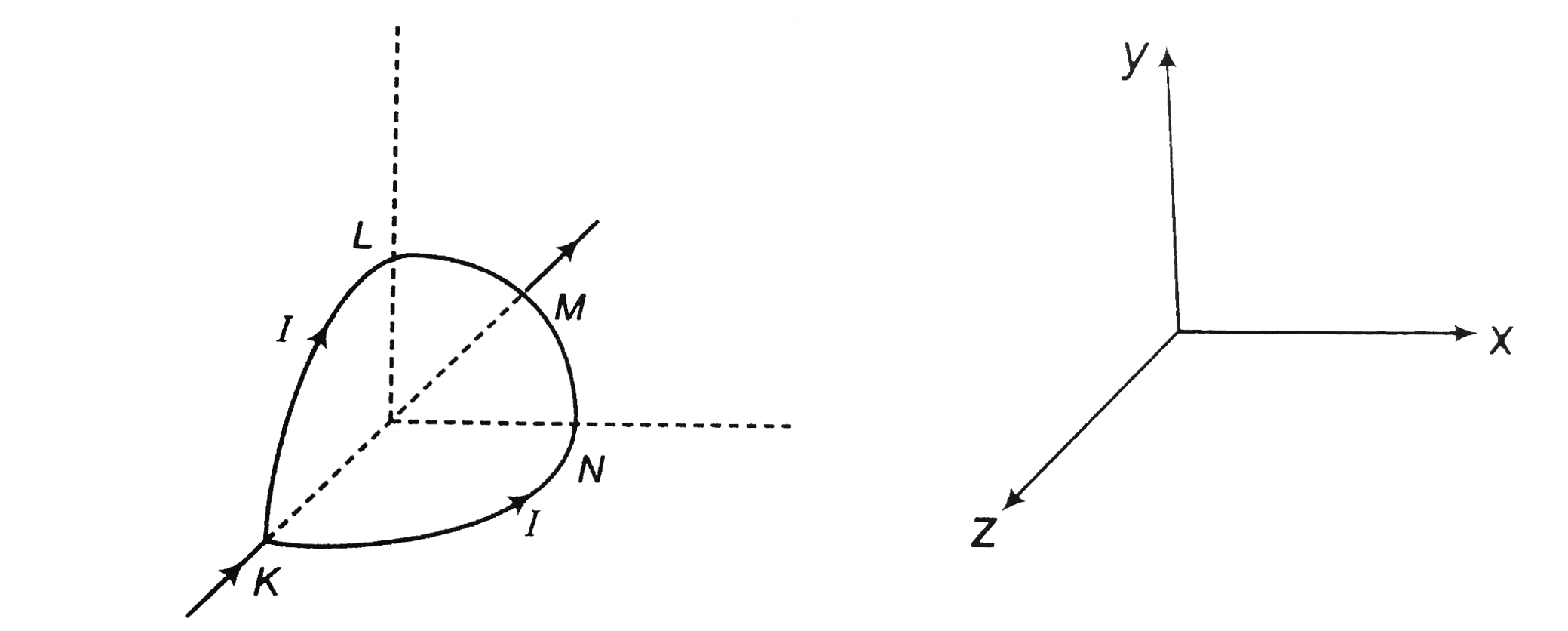
(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
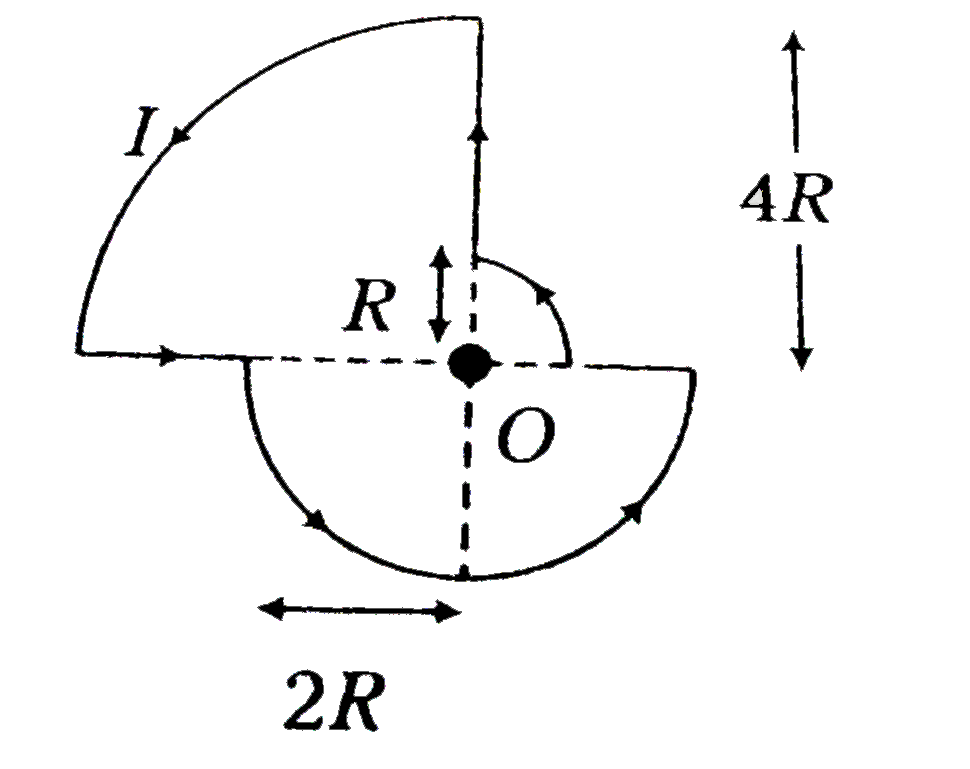
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
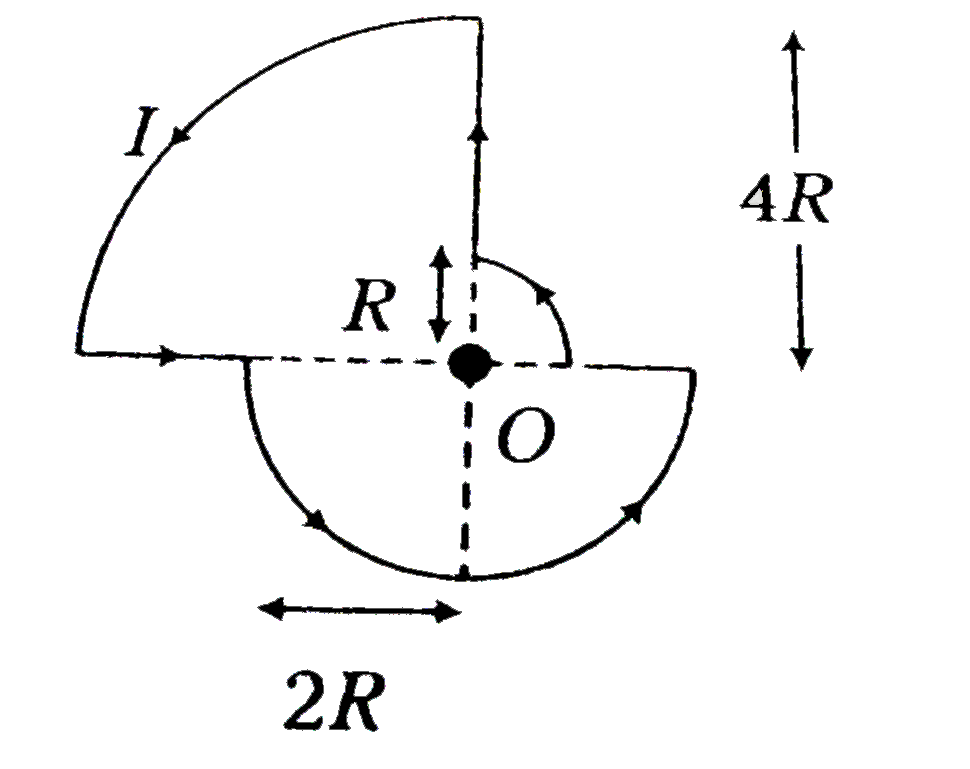
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
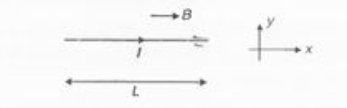
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View Solution