A plane spiral with a great number N of turns wound tightly to one another is located in a uniform magnetic field perpendicular to the spiral's plane.The outside radius of the spiral's turns is equal to a and inner radius is zero.The magnetic induction varies with time as B=B0sinωt, where B0 and ω are constants.The amplitude of emf induced in the spiral is εim=1xπa2NωB0.Find out value of x.
The correct Answer is:C
To solve the problem, we need to find the value of x in the expression for the amplitude of the induced EMF in a plane spiral located in a varying magnetic field.
1. Understanding the Problem:
We have a plane spiral with N turns, an outer radius a, and an inner radius of 0. The magnetic field B varies with time as B=B0sin(ωt).
2. Induced EMF:
The induced EMF ϵ in the spiral can be expressed using Faraday's law of electromagnetic induction:
ϵ=−NdΦdt
where Φ is the magnetic flux through the spiral.
3. Magnetic Flux Calculation:
The magnetic flux Φ through one turn of the spiral is given by:
Φ=B⋅A
where A is the area of the spiral. The area A of the spiral can be approximated as:
A=πr2
where r is the radius of the spiral.
4. Differentiating the Magnetic Field:
The magnetic field varies with time as B=B0sin(ωt). The rate of change of the magnetic field is:
dBdt=B0ωcos(ωt)
5. Substituting into the EMF Equation:
Substituting the expression for Φ into the EMF equation, we have:
ϵ=−Nddt(B0sin(ωt)⋅πr2)
This leads to:
ϵ=−N⋅πr2⋅dBdt
Substituting dBdt:
ϵ=−N⋅πr2⋅B0ωcos(ωt)
6. Integrating to Find the Amplitude:
To find the amplitude of the induced EMF, we consider the maximum value of cos(ωt), which is 1:
ϵmax=N⋅πa2⋅B0ω
Thus, the amplitude of the induced EMF is given by:
ϵim=NB0ωxπa2
7. Comparing with Given Expression:
We are given that:
ϵim=1xπa2NωB0
By comparing both expressions, we find:
x=3
Final Answer:
The value of x is 3.
We have a plane spiral with N turns, an outer radius a, and an inner radius of 0. The magnetic field B varies with time as B=B0sin(ωt).
The induced EMF ϵ in the spiral can be expressed using Faraday's law of electromagnetic induction:
ϵ=−NdΦdt
where Φ is the magnetic flux through the spiral.
The magnetic flux Φ through one turn of the spiral is given by:
Φ=B⋅A
where A is the area of the spiral. The area A of the spiral can be approximated as:
A=πr2
where r is the radius of the spiral.
The magnetic field varies with time as B=B0sin(ωt). The rate of change of the magnetic field is:
dBdt=B0ωcos(ωt)
Substituting the expression for Φ into the EMF equation, we have:
ϵ=−Nddt(B0sin(ωt)⋅πr2)
This leads to:
ϵ=−N⋅πr2⋅dBdt
Substituting dBdt:
ϵ=−N⋅πr2⋅B0ωcos(ωt)
To find the amplitude of the induced EMF, we consider the maximum value of cos(ωt), which is 1:
ϵmax=N⋅πa2⋅B0ω
Thus, the amplitude of the induced EMF is given by:
ϵim=NB0ωxπa2
We are given that:
ϵim=1xπa2NωB0
By comparing both expressions, we find:
x=3
The value of x is 3.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 4
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View Solution
Knowledge Check
A conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1mms−1. The induced emf when the radius is 2cm is
A2πμVBπμVCπ2μVD2μV
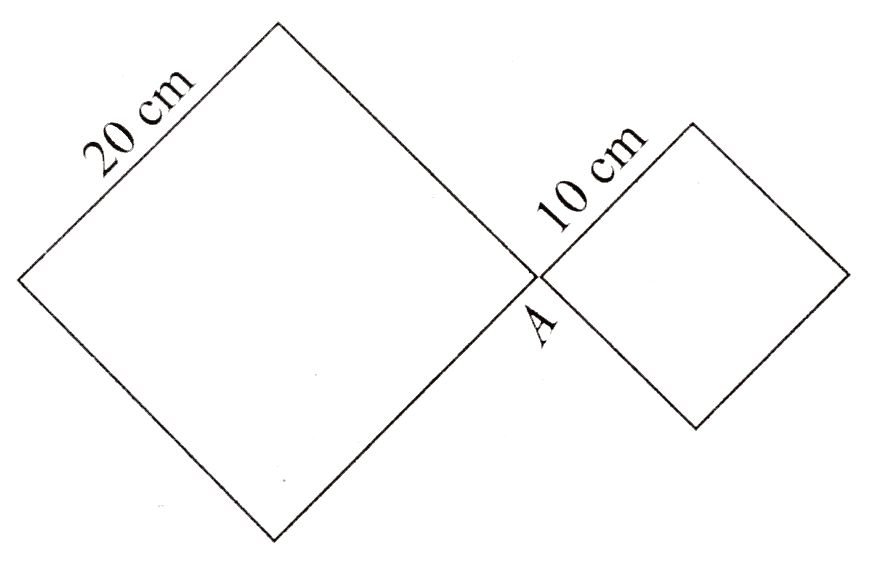
A plane loop is shaped as two squares (Fig) and placed in a uniform magnetic field at right angle to the loop's plane. The magnetic induction varies with time as B=B0sin(ω)t,whereB0=10mTand(ω)=100rads−1. The wires do not touch at point A. If resistance per unit length of the loop is 50m(Ω)/m, then amplitude of current induced in the loop is
View SolutionRadius of a circular ring is changing with time and the coil is placed in uniform magnetic field perpendicular to its plane. The variation of 'r' with time 't' is shown in Fig. Then induced emf e with time t will be best represented by
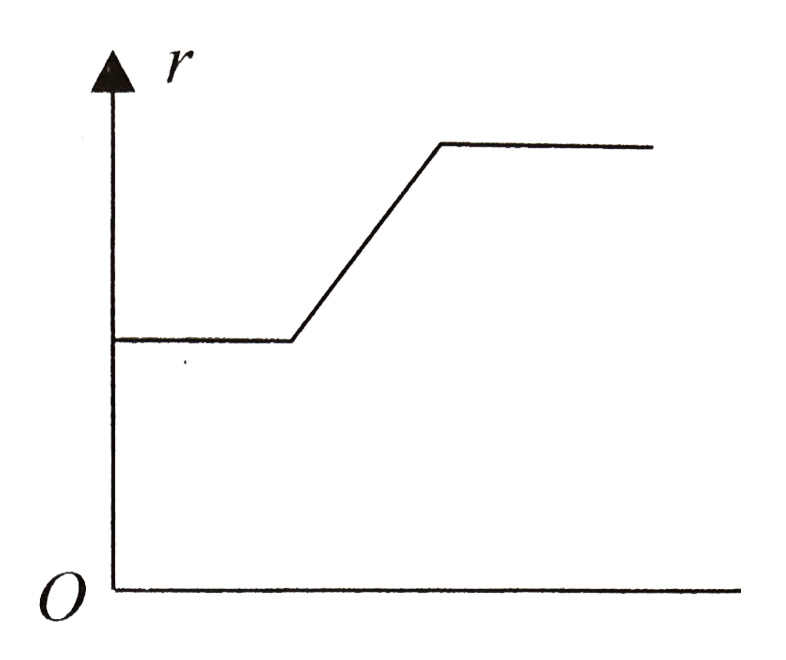
View SolutionRadius of a circular ring is changing with time and the coil is placed in uniform magnetic field perpendicular to its plane. The variation of 'r' with time 't' is shown in Fig. Then induced emf e with time t will be best represented by

View SolutionRadius of a circular ring is changing with time and the coil is placed in uniform magnetic field perpendicular to its plane. The variation of 'r' with time 't' is shown in Fig. Then induced emf e with time t will be best represented by

View SolutionA conducting ring of radius ris placed perpendicularly inside a time varying magnetic field given by B=B0+αl. B0 and a are positive constants. E.m.f. induced in the ring is
View SolutionShell is spiral in
View SolutionA copper disc of radius 0.1 m is rotated about its natural axis with 10 rps in a uniform magnetic field of 0.1 T with its plane perpendicular to the field, The emf induced across the radius of the disc is
View Solution
