A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

2π(R0+t)B clockwise
π(R0+t)B clockwise
2π(R0+t)B anticlockwise
zero
The correct Answer is:C
GivenR=(R0)+t
A=πR2=π(R0+t)2,dAdt=2π(R0+t)
therefore, emf induced in the loop is
e=BdAdt=2π(R0+t)B
Since area is increasing, induced emf is in anticlockwise sense to oppose the chang in flux.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
A circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
The figure shows a non conducting ring of radius R carrying a charge q. In a circular region of Radius r, a uniform magnetic field B perpendicular to the plane of the ring varies at a constant rate dBdt=β. The torque on the ring is

View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionThe figure shows a conducting ring of radius R. A uniform steady magnetic field B lies perpendicular to the plane of the ring a circular region r(<R). If the resistance per unit length of the ring is λ, then the current induced in the ring when its radius gets doubled is

View SolutionA superconducting loop of radius R has self inductance L.A uniform & constant magnetic field B is applied perpendicular to the plane of the loop. Initially current in this loop is zero. The loop is rotated about its diameter by 180∘.Find the current in the loop after rotation.
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is a constant and t is time. The induced current flowing through loop is
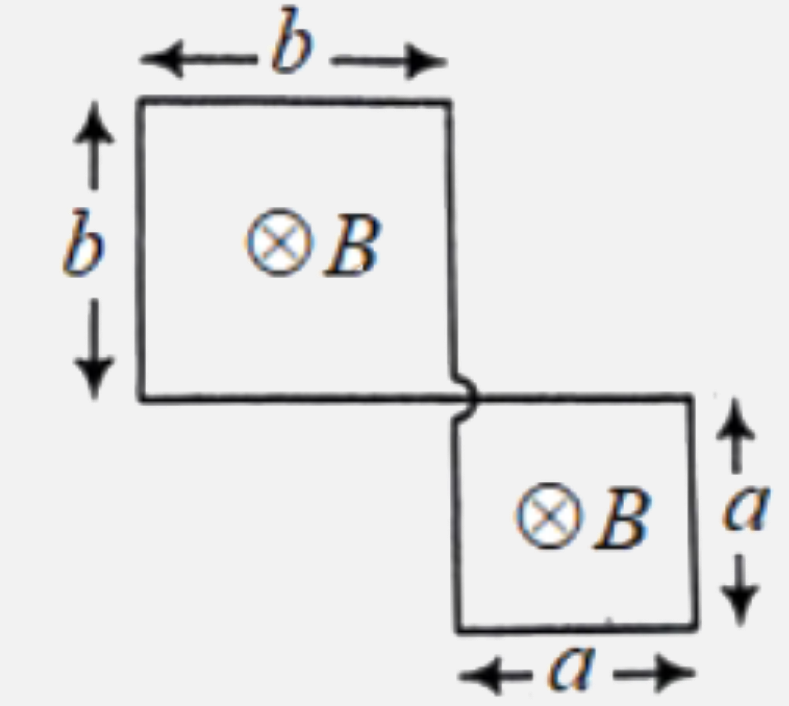
View SolutionA metal rod of resistance R is fixed along a diameter of a conducting ring of radius r. There is a magnetic field of magnitude B perpendicular to the plane of the loop. The ring spins with an angular velocity ω about its axis. The centre of the ring is joined to its rim by an external wire W. The ring and W have no resistance. The current in W is
View Solution
