At any instant a current of 2 A is increasing at a rate of 1A/s through a coil of indcutance 2 H. Find the energy (in SI units) being stored in the inductor per unit time at that instant.
The correct Answer is:4
U=12Li2
Energy stroed per unit time
dUdt=12L2ididt=Lididt=2×2×1=4J/s.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
A current of 2A is increasing at a rate of 4As−1 through a coil of inductance 1H. Find the energy stored in the inductor per unit time in the units of Js−1.
View SolutionA current of 2A is increasing at a rate of 4A/s through a coil of inductance 2H. The energy stored in the inductor per unit time is
View Solution
Knowledge Check
A current of 1 A through a coil of inductance of 200 mH is increasing at a rate of 0.5As−1. The energy stored in the inductor per second is
A0.5Js−1B5.0Js−1C0.1Js−1D2.0Js−1
A current of 2A is increasing at a rate of 4A/s through a coil of inductance 2H. The energy stored in the inductor per unit time is
View SolutionThe figure shows a part of a complete circuit. At the instant shown, the current i=2A and it is decreasing at rate 2×103A/s. Find the potential difference between A and B and energy stored in the magnetic field at this instant. VA−12+3i+15+5i+Ldidt+2i=VB

View SolutionTwo different coils have self- inductances L1=16 mH and L2=12mH. At a certain instant, the current in the two coils is increasing at the same rate and power supplied to the two coils is the same. Find the ratio of i) induced voltage ii) current iii) energy stored in the two coils at that instant.
View SolutionOn passing a current of 2A in a coil inductance 5H, the energy stored in it will be-
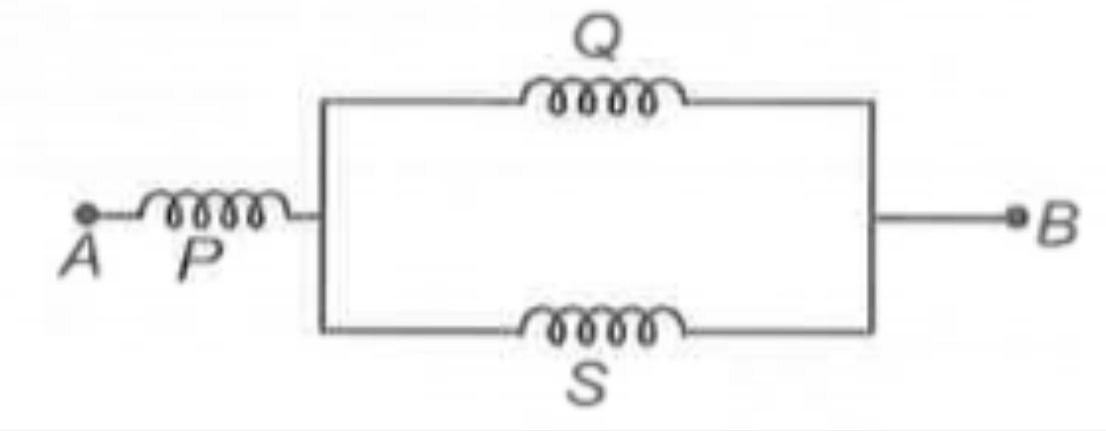
View SolutionThree identical inductors are connected as shown in the figure. At the instant when current in inductor P is increasing at the rate of 0.0320 As−1 then magnitude of induced emf in it is 0.080 V. The equivalent inductance between the points A and B will be
View SolutionTwo coils having self-inductances, L1=5mH and L2=1mH. The current in the coil is increasing of same constant rate at a certain instant and the power supplied to the coils is also same, Find the ratio of
(i) induced voltage
(ii) current
(iii) energy stored in two coils at that instant
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t

View Solution
