A magnetic field induction is changing in magnitude at a constant rate dB/dt . A given mass m of copper is drawn into a wire of radius α and formed into a loop of radius r is placed perpendicular to the field. Show that induced current in the loop is given by i=m4πpδdBdt
p : resistivity, δ : density of copper.
The correct Answer is:A, B, D
To solve the problem, we need to derive the expression for the induced current i in a loop formed from a given mass m of copper, which is subjected to a changing magnetic field B at a constant rate dBdt.
1. Understanding the Setup:
- We have a mass m of copper that is drawn into a wire of radius α and formed into a loop of radius r.
- The loop is placed perpendicular to a magnetic field B that is changing at a rate dBdt.
2. Calculate the Length of the Wire:
- The length L of the wire used to form the loop is equal to the circumference of the loop:
L=2πr
3. Calculate the Volume of Copper:
- The volume V of the copper wire can be expressed in terms of its length and cross-sectional area:
V=A⋅L=πα2⋅L
- Substituting L:
V=πα2(2πr)=2π2rα2
4. Relate Mass, Density, and Volume:
- The mass m of the copper can be expressed using its density δ:
m=δV=δ(2π2rα2)
5. Calculate the Resistance of the Wire:
- The resistance R of the wire can be calculated using the resistivity p:
R=pLA=p(2πr)πα2=2prα2
6. Calculate the Induced EMF:
- The induced EMF E in the loop due to the changing magnetic field is given by Faraday's law:
E=−dΦdt
- The magnetic flux Φ through the loop is:
Φ=B⋅A=B⋅πr2
- Therefore, the induced EMF becomes:
E=−πr2dBdt
7. Calculate the Induced Current:
- The induced current i can be calculated using Ohm's law:
i=ER
- Substituting the expressions for E and R:
i=−πr2dBdt2prα2=−πr2α22prdBdt
- Simplifying this gives:
i=−πrα22pdBdt
8. Substituting for r:
- From the mass equation, we can express r in terms of m:
m=2π2rα2δ⟹r=m2π2α2δ
- Substitute r back into the current expression:
i=−π(m2π2α2δ)α22pdBdt
- Simplifying this gives:
i=−m4πpδdBdt
9. Final Result:
- Thus, the induced current i in the loop is given by:
i=m4πpδdBdt
- We have a mass m of copper that is drawn into a wire of radius α and formed into a loop of radius r.
- The loop is placed perpendicular to a magnetic field B that is changing at a rate dBdt.
- The length L of the wire used to form the loop is equal to the circumference of the loop:
L=2πr
- The volume V of the copper wire can be expressed in terms of its length and cross-sectional area:
V=A⋅L=πα2⋅L
- Substituting L:
V=πα2(2πr)=2π2rα2
- The mass m of the copper can be expressed using its density δ:
m=δV=δ(2π2rα2)
- The resistance R of the wire can be calculated using the resistivity p:
R=pLA=p(2πr)πα2=2prα2
- The induced EMF E in the loop due to the changing magnetic field is given by Faraday's law:
E=−dΦdt
- The magnetic flux Φ through the loop is:
Φ=B⋅A=B⋅πr2
- Therefore, the induced EMF becomes:
E=−πr2dBdt
- The induced current i can be calculated using Ohm's law:
i=ER
- Substituting the expressions for E and R:
i=−πr2dBdt2prα2=−πr2α22prdBdt
- Simplifying this gives:
i=−πrα22pdBdt
- From the mass equation, we can express r in terms of m:
m=2π2rα2δ⟹r=m2π2α2δ
- Substitute r back into the current expression:
i=−π(m2π2α2δ)α22pdBdt
- Simplifying this gives:
i=−m4πpδdBdt
- Thus, the induced current i in the loop is given by:
i=m4πpδdBdt
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A magnetic field induction is changing in magnitude in a region at a constant rate dB/dt. A given mass m of copper drawn into a wire and formed into a loop is placed perpendicular to the field. If the values of specific resistance and density of copper are ρ and σ respectively, then the current in the loop is given by :
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View Solution
Knowledge Check
A unifrom magnetic field B points vertically up and is slowly changed in magnitude, but not in direction. the rate of change of the magnetic field is α .A conducting ring of radius r and resistance R is held perpendicular to the megnetic field, and is totally inside it. The induced current in the ring is
AzeroB2πeBRCrαRDπr2αRA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
The magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionIn Fig. a uniform magnetic field decrease at a constant rate dB/dt=K, where K is a positive constant. Circular loop of wire of radius a containing a resistnce R and a capacitnce C is placed with its plane normal to the field.
a. Find the charge Q on the capacitor when it is fully charged.
b. Which plate is at higher potential when it is fully charged?

View SolutionA uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :
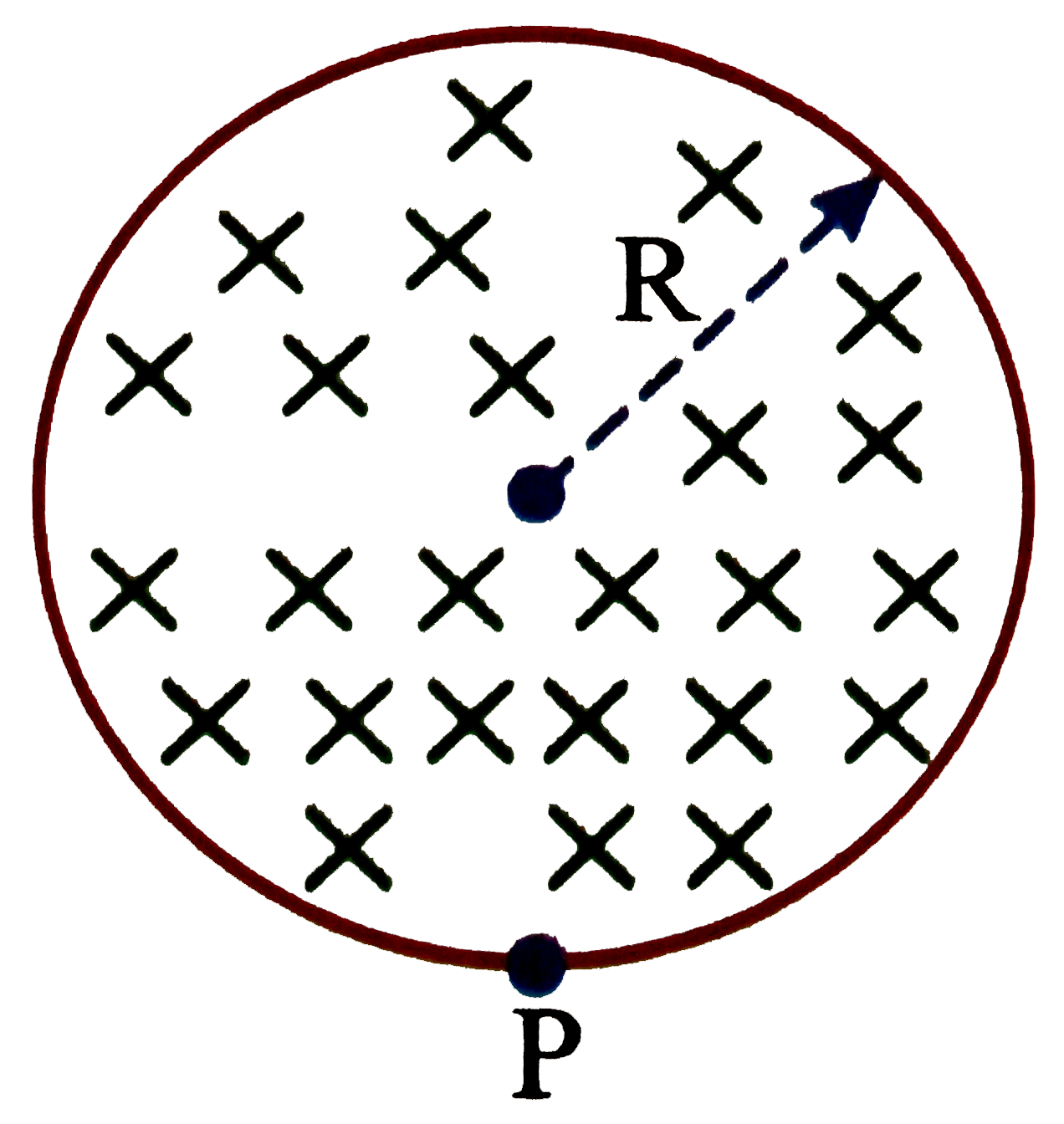
View SolutionA uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :

View SolutionA square wire loop of side 30cm & wire cross section having diameter 4mm is placed perpendicular to a magnetic field changing at the rate 0.2 T/s. Final induced current in the wire loop.
(Given: Resistivity of wire material is (1.23×10−8ohmm)
View Solution
