A flexible wire loop in the shape of a circle has a radius that grows linearly with time. There is a magnetic field perpendicular to the plane of the loop that has a magnitude inversely proportional to the distance from the centre of the loop, B(r)∝1r How does the emf E vary with time?
(a) E∝t2
(b) E∝t
( c) E∝√t
(d) E is constant
The correct Answer is:D
To solve the problem, we need to analyze how the electromotive force (emf) E varies with time as the radius of the circular wire loop changes and as the magnetic field behaves according to the given conditions.
1. Understanding the Problem:
- We have a circular loop with radius r that increases linearly with time, r(t)=ct where c is a constant.
- The magnetic field B is inversely proportional to the distance from the center of the loop, i.e., B(r)∝1r.
2. Magnetic Flux Calculation:
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop. For a circle, the area A=πr2.
- Thus, we can express the magnetic flux as:
Φ=B⋅πr2
3. Substituting for Magnetic Field:
- Since B∝1r, we can write:
B=kr
where k is a proportionality constant.
- Therefore, the magnetic flux becomes:
Φ=kr⋅πr2=kπr
4. Finding the Induced EMF:
- The induced emf E is given by Faraday's law of electromagnetic induction:
E=−dΦdt
- We need to differentiate the magnetic flux with respect to time:
Φ=kπr⟹dΦdt=kπdrdt
5. Substituting for drdt:
- Since r(t)=ct, we have:
drdt=c
- Therefore, substituting this into the equation for dΦdt:
dΦdt=kπc
6. Final Expression for EMF:
- Thus, the induced emf is:
E=−dΦdt=−kπc
- Since k, π, and c are constants, the induced emf E is also a constant.
Conclusion:
The induced emf E does not vary with time; it remains constant.
- We have a circular loop with radius r that increases linearly with time, r(t)=ct where c is a constant.
- The magnetic field B is inversely proportional to the distance from the center of the loop, i.e., B(r)∝1r.
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop. For a circle, the area A=πr2.
- Thus, we can express the magnetic flux as:
Φ=B⋅πr2
- Since B∝1r, we can write:
B=kr
where k is a proportionality constant.
- Therefore, the magnetic flux becomes:
Φ=kr⋅πr2=kπr
- The induced emf E is given by Faraday's law of electromagnetic induction:
E=−dΦdt
- We need to differentiate the magnetic flux with respect to time:
Φ=kπr⟹dΦdt=kπdrdt
- Since r(t)=ct, we have:
drdt=c
- Therefore, substituting this into the equation for dΦdt:
dΦdt=kπc
- Thus, the induced emf is:
E=−dΦdt=−kπc
- Since k, π, and c are constants, the induced emf E is also a constant.
The induced emf E does not vary with time; it remains constant.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Multiple Correct
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Asserton - Reasoning
Explore 8 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Subjective
Explore 13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
Similar Questions
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conductig loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude fo the emf induced in the loop, greater first

View SolutionA flexible wire bent in the form of a circle is placed in a uniform magnetic field perpendicular to the plane of the circle, The radius r of circle changes with time t as shown in the figure. The graph of magnitude of induced emf |e| versus time in the circle is represented by
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is a constant and t is time. The induced current flowing through loop is
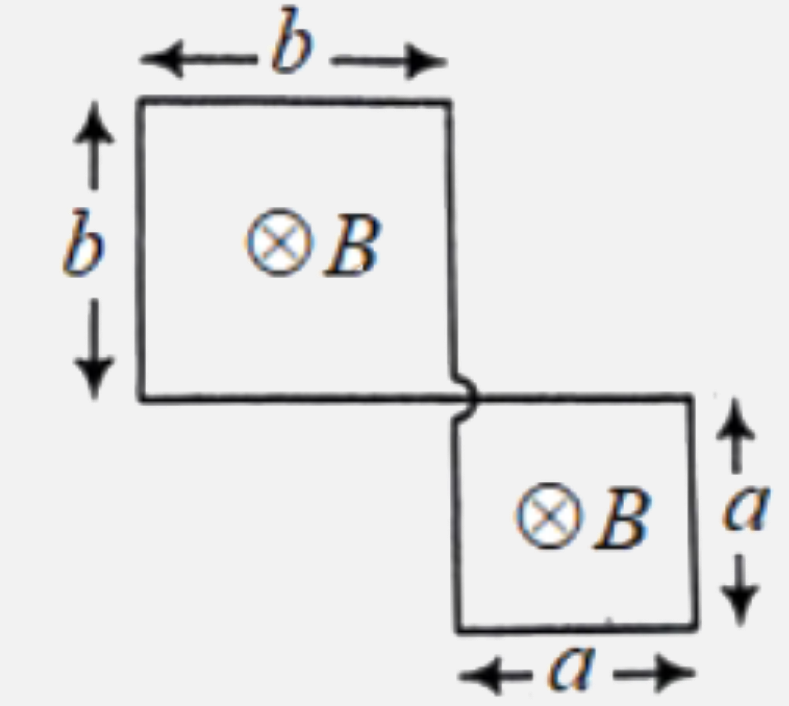
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is

View Solution