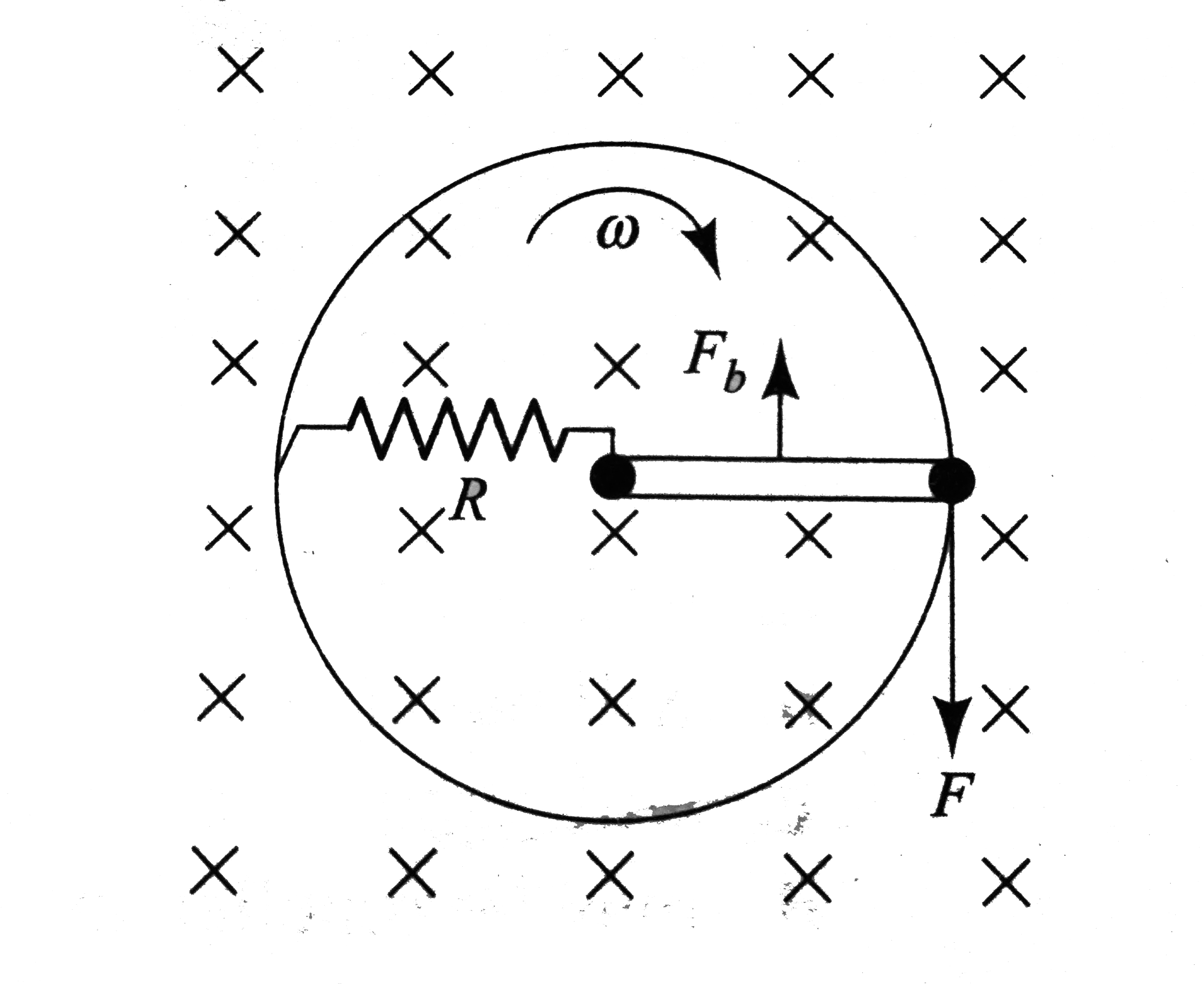
A metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
(a) B2ωr28R
(b) B2ωr22R
( c) B2ωr32R
(d) B2ωr34R
The correct Answer is:D
(d) Induced emf in the spoke is shown in figure below.

e=12Bωr2,I=eR=Bωr22R
There will be no induced emf separately in parts ADCor AEC.
Fb=IrB=B2ωr34R
balancing torque about E: Fr=Fbr/2
rarr F=Fb2=B2ωr34R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
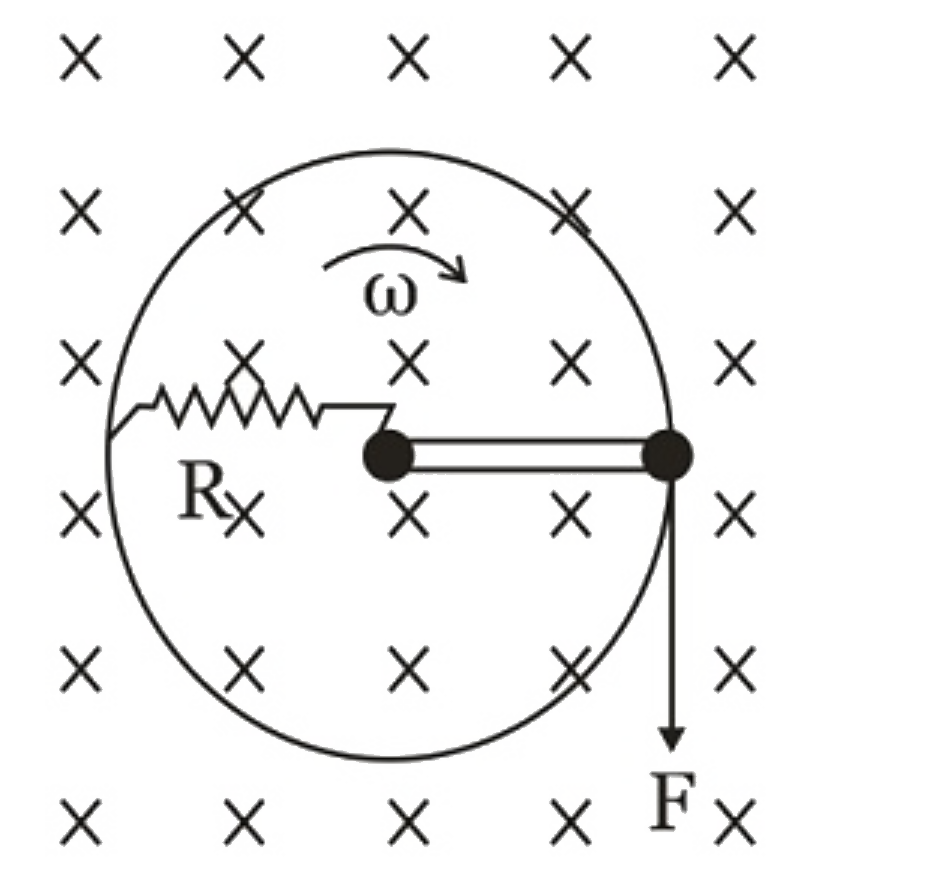
A metallic ring of mass 2 kg and radius 1 m with with a uniform metallic spoke of same mass 2 kg and length 1 m is rotated about its axis with angular velocity 1 rev sec−1. In a perpendicular uniform magnetic field B of magnitude 10 T as shown in the figure. If the central end of the spoke is connected to the rim of the wheel through a resistor R of magnitude πΩ as shown. The resistor does not rotate, It's one end is always at the centre of the ring and another end is always in contact with the ring. A force F as shown is needed to maintain the constant angular velocity of the spoke then, F is equal to (The ring and the spoke has zero resistance)
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity o. If o increases then tension in ring
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is

View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View Solution
