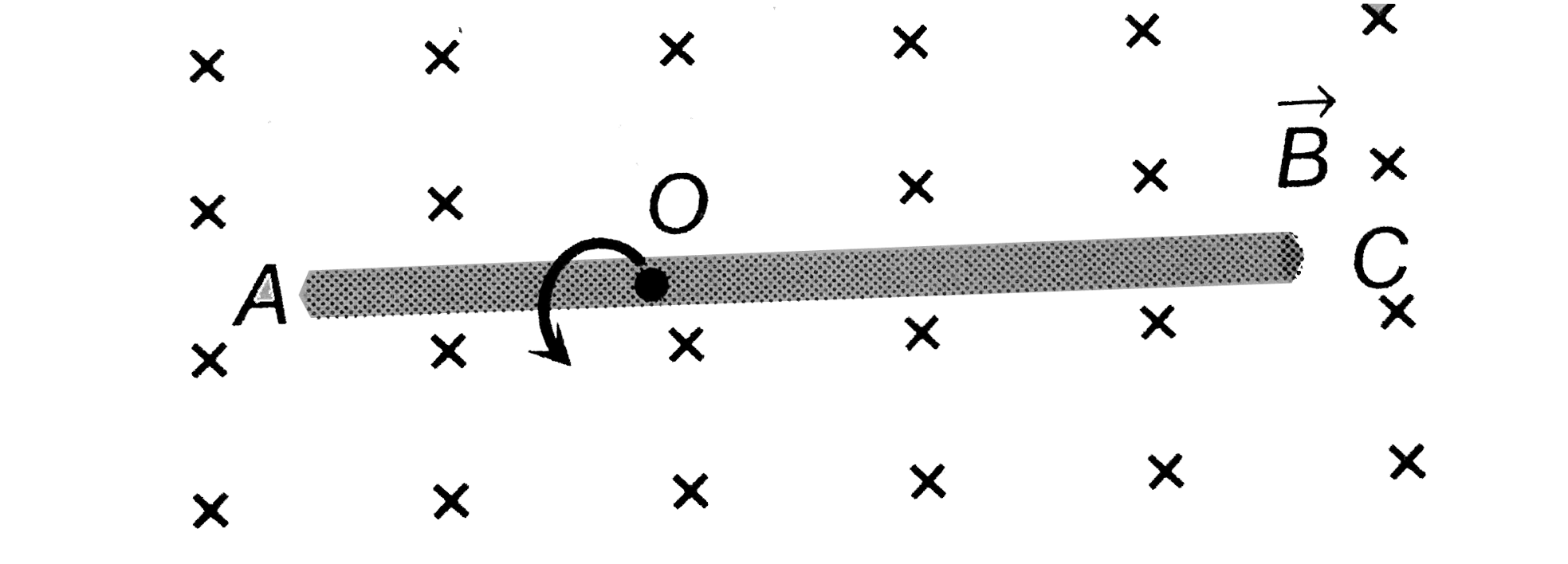
A conducting rod OA of length l is rotated about its end O with an angular velocity in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
To find the induced electromotive force (emf) in a conducting rod OA of length l that is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicular to the rotation, we can follow these steps:
Step 1: Understand the Setup
We have a conducting rod OA of length l rotating about point O with angular velocity ω. The magnetic field B is uniform and directed perpendicular to the plane of rotation.
Step 2: Define a Small Element
Consider a small section of the rod at a distance x from point O with a width dx. We will analyze this small section to find the induced emf.
Step 3: Calculate Linear Velocity
The linear velocity v of the small section at distance x from O can be expressed as:
v=x⋅ω
This is derived from the relationship v=r⋅ω, where r is the distance from the axis of rotation.
Step 4: Induced emf in the Small Element
The induced emf dE in the small section dx can be calculated using the formula for motional emf:
dE=B⋅v⋅dx
Substituting the expression for v:
dE=B⋅(x⋅ω)⋅dx
Step 5: Integrate to Find Total emf
To find the total induced emf E in the entire rod from O to A, we integrate dE from x=0 to x=l:
E=∫l0B⋅(x⋅ω)⋅dx
This simplifies to:
E=B⋅ω⋅∫l0xdx
Step 6: Evaluate the Integral
The integral ∫l0xdx can be computed as:
∫l0xdx=(x22)l0=l22
Substituting this back into the expression for E:
E=B⋅ω⋅l22
Step 7: Final Result
Thus, the induced emf E in the rod is given by:
E=12Bωl2
Step 8: Direction of Induced Current
Using the right-hand rule, we can determine the direction of the induced current. If the fingers of the right hand point in the direction of the magnetic field and the thumb points in the direction of the velocity of the rod, the palm will face in the direction of the induced current. This indicates that point A will be at a higher potential than point O.
We have a conducting rod OA of length l rotating about point O with angular velocity ω. The magnetic field B is uniform and directed perpendicular to the plane of rotation.
Consider a small section of the rod at a distance x from point O with a width dx. We will analyze this small section to find the induced emf.
The linear velocity v of the small section at distance x from O can be expressed as:
v=x⋅ω
This is derived from the relationship v=r⋅ω, where r is the distance from the axis of rotation.
The induced emf dE in the small section dx can be calculated using the formula for motional emf:
dE=B⋅v⋅dx
Substituting the expression for v:
dE=B⋅(x⋅ω)⋅dx
To find the total induced emf E in the entire rod from O to A, we integrate dE from x=0 to x=l:
E=∫l0B⋅(x⋅ω)⋅dx
This simplifies to:
E=B⋅ω⋅∫l0xdx
The integral ∫l0xdx can be computed as:
∫l0xdx=(x22)l0=l22
Substituting this back into the expression for E:
E=B⋅ω⋅l22
Thus, the induced emf E in the rod is given by:
E=12Bωl2
Using the right-hand rule, we can determine the direction of the induced current. If the fingers of the right hand point in the direction of the magnetic field and the thumb points in the direction of the velocity of the rod, the palm will face in the direction of the induced current. This indicates that point A will be at a higher potential than point O.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Try Yourself
Explore 42 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Assignment (SECTION - A)
Explore 55 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:comprehension
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
Similar Questions
A conducting rod AB of length l is rotated about point O with an angular velocity velocity omega in a uniform magnetic field (B_0) directed perpendicular into the plane of rotation as shown in the figure. The value of VB−VA is
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA metal rod length l rotates about on end with a uniform angular velocity ω. A uniform magnetic field →B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they moving in circular paths.
View SolutionA conducting rod AC of length 4l is rotate about a point O in a uniform magnetic field →B directed into the paper. AO=l and OC=3l. Then
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
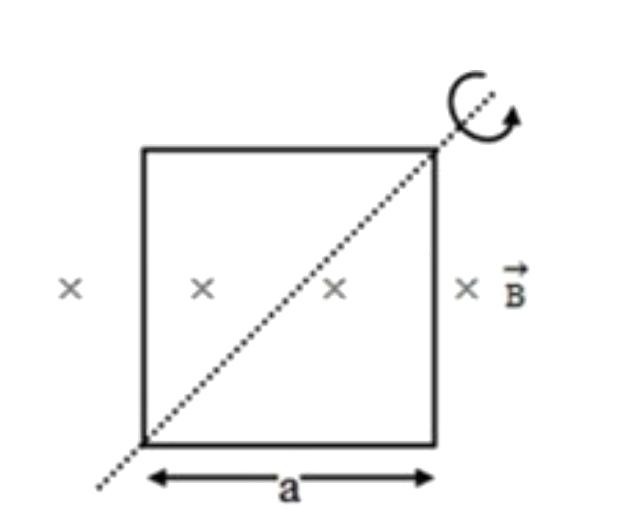
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View Solution